2. Примеры

Пример 1. Функция алгебры логики трех переменных f(x₁,x₂,x₃)=1 лишь при следующем наборе значений логических переменных:

х1	х2	х3
0	0	0
1	0	1
1	1	1

Найти аналитическое выражение функции, оптимизировать её.

Решение

Так как функция равна 1 на трех из восьми возможных наборов значений переменных, то СДНФ рассматриваемой функции имеет вид:

.

Сгруппируем второе и третье дизъюнктивные слагаемые, вынесем за скобки общий множитель и в соотсетствии с равенством , получим:

.

Учитывая, что , приходим к следующему результату:

.

Если для реализации функции, полученной по СДНФ, необходимо выполнить 12 логических операций, то после оптимизации достаточно только шесть.

Пример 2. Функция алгебры логики трех переменных f(x₁,x₂,x₃)=0 лишь при следующем наборе значений логических переменных:

х1	х2	х3
1	0	1
1	1	0
1	1	1

Найти оптимальное аналитическое выражение функции.

Решение

Количество наборов переменных, при которых значение функции равно 0 значительно меньше числа наборов значений переменных, при которых значение функции равно 1. Поэтому для решения задачи применим СКНФ. Тогда

.

Выполним преобразования. Обозначим . Тогда

= .

Таким образом, .

Раскрыв скобки, получим:

.

Окончательно получаем .

Для реализации функции алгебры логики, полученной с помощью СКНФ, необходимо выполнить 16 логических операций, а после оптимизации достаточно всего четыре.

4.3 Варианты задачи №6

Составить таблицы истинности формул

1. ; .

2. ; .

3. ; .

4. ; .

5. ; .

6. ; .

7. ; .

8. ; .

9. ; .

10. ; .

11. ; .

12. ; .

13. ; .

14. ; .

15. ; .

16. ; .

17. ; .

18. ; .

19. ; .

20. ; .

21. ; .

22. ; .

23. ; .

24. ; .

25. ; .

26. ; .

27. ; .

28. ; .

29. ; .

30. ; .

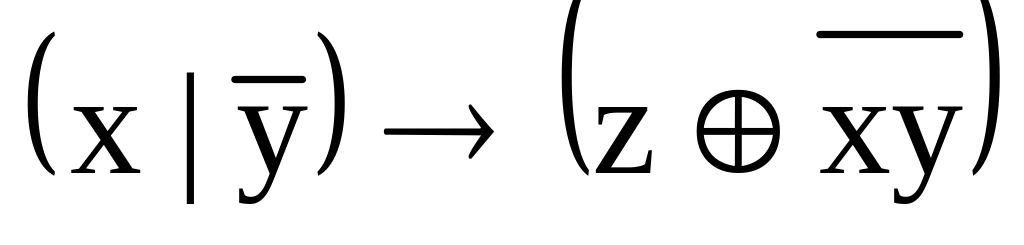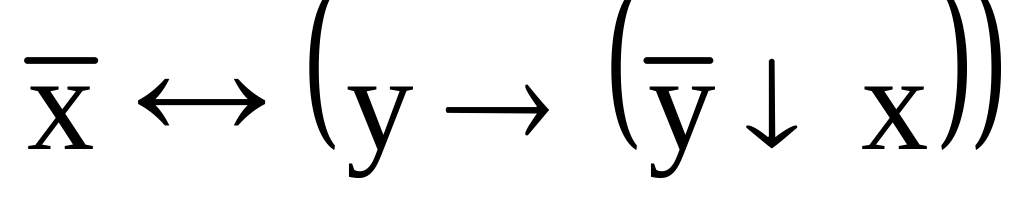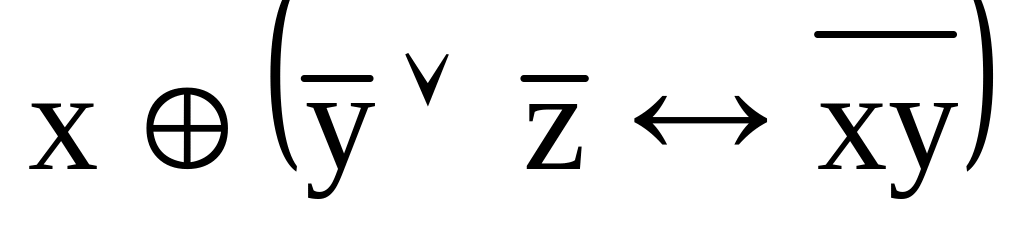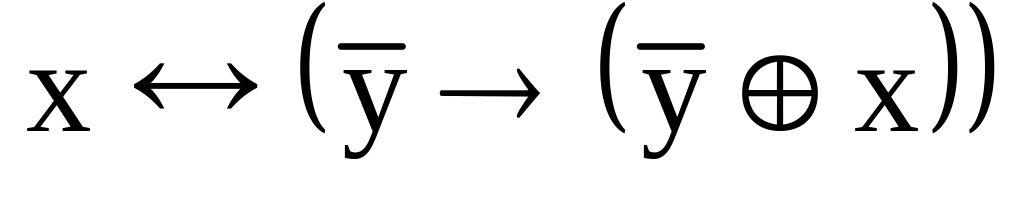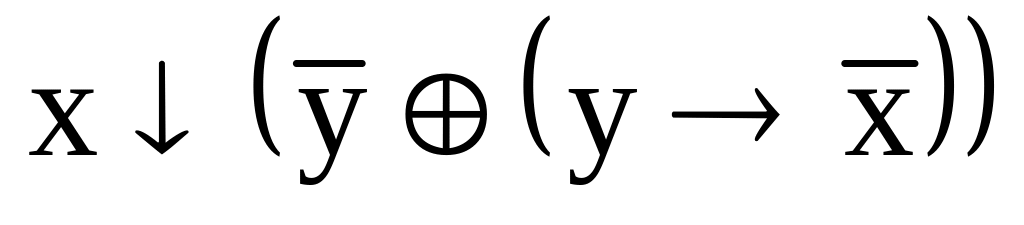4.4 Варианты задачи №7

Проверить двумя способами, будут ли эквивалентны указанные в вариантах формулы:

а) составлением таблиц истинности;

б) приведением к СДНФ или СКНФ с помощью эквивалентных преобразований

1. и .

2. и .

3. и .

4. и .

5. и .

6. и .

7. и .

8. и .

9. и .

10. и .

11. и .

12. и .

13. и .

14. и .

15. и .

16. и .

17. и .

18. и .

19. и .

20. и .

21. и .

22. и .

23. и .

24. и .

25. и .

26. и .

27. и .

28. и .

29. и .

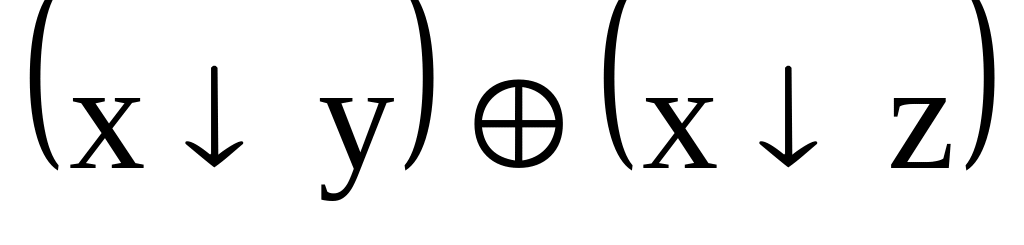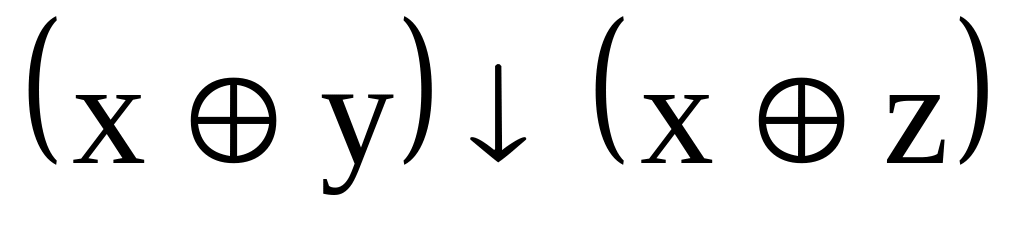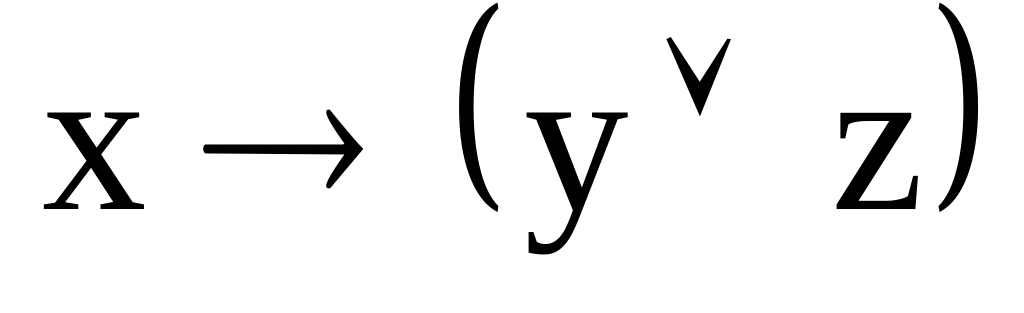30. и .

4.5 Варианты задачи №8

В вариантах 1-15 найти оптимальное аналитическое выражение функции алгебры логики, применяя СДНФ, если она равна 1 лишь при указанных в таблице наборах логических переменных, а в остальных случаях 0.

Таблица 8 – Варианты задачи №8

Пе- рем.	Варианты
	1	2	3	4	5	6	7	8	9	10
х1 х2 х3	001	001	001	000	001	011	011	011	000	111
х1 х2 х3	001	001	000	011	011	100	110	100	011	001
х1 х2 х3	010	011	011	101	100	110	100	101	101	010

Продолжение таблицы 8

Пе- рем.	Варианты
	11	12	13	14	15
х1 х2 х3	000	000	001	011	111
х1 х2 х3	001	011	110	100	001
х1 х2 х3	010	101	010	101	010

В вариантах 16-30 найти оптимальное аналитическое выражение функции алгебры логики, применяя СКНФ, если она равна 0 лишь при указанных в таблице наборах логических переменных, а в остальных случаях 1:

Продолжение таблицы 8

Пе- рем.	Варианты
	16	17	18	19	20	21	22	23	24	25
х1 х2 х3	000	000	001	011	111	111	000	001	011	111
х1 х2 х3	001	011	110	100	001	011	011	110	100	001
х1 х2 х3	010	101	010	101	010	101	001	010	101	011

Продолжение таблицы 8

Пе- рем.	Варианты
	26	27	28	29	30
х1 х2 х3	001	001	001	000	001
х1 х2 х3	001	001	000	011	011
х1 х2 х3	010	011	011	101	100