5. Основы теории графов

1. Основные понятия и формулы

Граф G(X,Г) задан, если заданы непустое множество X=(x₁,x₂,...,x_n) и многозначное отображение Г множества Х во множество Х.

Многозначное отображение Г – это закон, по которому каждому элементу x_iX ставится в соответствие некоторое подмножество (может быть ) Гх_i  Х.

Элементы множества Х (изображаются точками, кружочками, квадратиками) называются вершинами графа.

Элементы отображения Г (изображаются линиями произвольной формы, соединяющими элемент х с элементами подмножества Г_х) называются ребрами.

Если на каждом ребре задано направление, то граф G называется ориентированным или орграфом, в противном случае - неориентированным. В орграфе ребра называются дугами.

Смешанным называется граф, содержащий и ребра, и дуги.

Нуль-графом называется граф, состоящий из изолированных вершин, не соединенных ребрами или дугами.

Орграф называется симметрическим, если для любых двух вершин x_i, x_j из того, что x_ix_j, следует, что x_jx_i. Если это условие не соблюдается, то граф называется асимметрическим.

Ребра, имеющие одинаковые концевые вершины, называются параллельными или кратными.

Ребро, концевые вершины которого совпадают, называется петлей.

Граф G, в котором некоторые пары вершин соединены более чем одним ребром (или кратными дугами), называется мультиграфом.

Мультиграф, имеющий петли, называется псевдографом.

Вершина и ребро называются инцидентными друг другу, если вершина является концевой для этого ребра.

Две вершины, являющиеся концевыми для некоторого ребра, называются смежными.

Два ребра, инцидентные одной вершине, называются смежными.

На рисунке 2 ребра а₃ и а₄ – параллельные, а₂ – петля, вершина х₃ и ребро а₆ инцидентны друг другу, х₀ и х₁ – смежные вершины, а₁, а₃ и а₄ – смежные ребра.

С

х₄

тепенью  вершины называется число ребер, инцидентных ей. Вершина степени 0 (вершина х₄ на рисунке 2) называется изолированной.

Рисунок 2 – Пример

неориентированного графа

Вершина степени 1 (вершина х₃ на рисунке 2) называется висячей.

В графе G сумма степеней всех его вершин равна удвоенному числу его ребер: где n – число вершин графа, _i – степень i–той вершины графа, m – число ребер графа.

Число нечетных вершин (имеющих нечетную степень) любого графа четно.

Граф G называется полным, если любые две его различные вершины соединены ребром, и он не содержит параллельных ребер.

Дополнением графа G называется граф G с теми же вершинами, что и граф G, и содержащий только те ребра, которые нужно добавить к графу G, чтобы получился полный граф (рисунок 3).

Рисунок 3 – Граф G и его дополнение G

Путем в графе называется такая последовательность ребер, ведущая от некоторой начальной вершины х₀ в конечную вершину х_n, в которой каждые два соседних ребра имеют общую вершину и никакое ребро не встречается более одного раза.

Циклом называется путь, начальная и конечная вершины которого совпадают.

Цепью в орграфах называется такая последовательность дуг, ведущих от вершины х₀ к вершине х_n, в которой каждые две соседние дуги имеют общую вершину и никакая дуга не встречается более одного раза. Если направление цепи совпадает с направлением всех принадлежащих ей дуг, то цепь называется путем.

В орграфах циклом называется путь, начало и конец которого совпадают.

Цепь, путь, цикл в произвольном графе G называются простыми, если они не проходят ни через одну свою вершину более одного раза.

Длиной цепи, пути, цикла в произвольном графе G называется число содержащихся в них дуг (ребер).

Сетью называется граф, каждой дуге (или вершине) которого поставлено в соответствие некоторое число или несколько чисел.

Граф G называется связным, если для любых его двух вершин существует соединяющий их путь. В противном случае граф называется несвязным.

Любой несвязный граф G является совокупностью связных графов, каждый из которых называется компонентой графа G.

Для того чтобы граф G представлял собой простой цикл, необходимо и достаточно, чтобы каждая его вершина имела степень 2.

Ребро  называется мостом графа G, если граф G\, полученный

из графа G после удаления ребра , содержит больше компонент, чем граф G.

Ребро  графа G является мостом тогда и только тогда, когда  не принадлежит ни одному циклу.

Граф G(X,A) называется подграфом графа G(X,A), если ХХ и АА, причем ребро содержится в А только в том случае, если его концевые вершины содержатся в Х.

Граф G(X,A) называется вершинопорожденным подграфом графа G(X,A).

Граф G(X,A) называется реберно-порожденным подграфом графа G(X,A).

Объединением графов G₁(X₁,A₁) и G₂(X₂,A₂) называется граф G(Х,А)=G₁G₂, множество вершин которого есть Х=Х₁Х₂, а множество ребер А=А₁А₂.

Пересечением графов G₁(X₁,A₁) и G₂(X₂,A₂) называется граф G(X,A)=G₁G₂, множество вершин которого есть Х=Х₁Х₂, а множество ребер А=А₁А₂.

Кольцевой суммой двух графов G₁(Х₁,А₁) и G₂(Х₂,А₂) называется граф G(Х,А)=G₁G₂, порожденный на множестве ребер, не принадлежащих их пересечению: А=(А₁А₂)\(А₁А₂).

Связный граф, не содержащий циклов, называется деревом.

Деревом некоторого графа G называется его связный подграф без циклов.

Граф, не содержащий циклов и состоящий из к компонент, называется к-деревом.

Остовом Т графа G (покрывающим деревом) называется дерево графа, содержащее все его вершины.

к-дерево графа G, содержащее все его вершины, называется остовным.

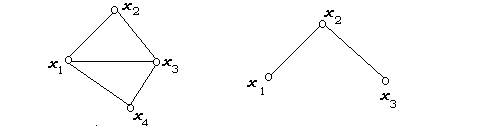
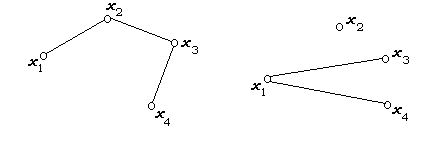
Кодеревом Т^* остова Т графа G называется такой подграф G, который содержит все его вершины и только те ребра, которые не входят в Т (рисунок 4).

G G₁

Т Т^*

Рисунок 4 – Граф G, его дерево G₁, остов Т и кодерево Т^*

Граф G c n вершинами является деревом тогда и только тогда, когда он связный и число его ребер равно n-1.

Ребра остова Т обычно называют ветвями, а ребра кодерева Т^*- связями.

Граф G является деревом тогда и только тогда, когда он не содержит циклов, и при соединении ребром двух произвольных несмежных его вершин получается граф, имеющий ровно один цикл.

Подграф графа G, содержащий все его вершины и только те ребра, которые не входят в остовное к-дерево Т графа G, называется к-кодеревом Т^* (рисунок 5).

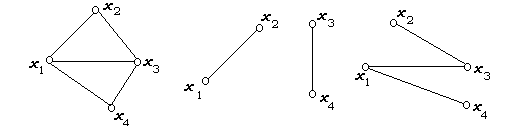G Т Т^*

Рисунок 5 – Граф G, его остовное 2-дерево Т, 2-кодерево Т^*

графа G

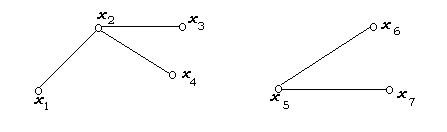
Если граф G содержит к компонент, то его остовное к-дерево называется лесом, а к-кодерево Т^* называется КО-лесом (рисунок 6).

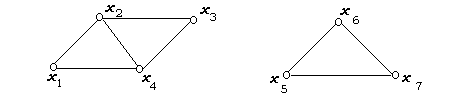G

Т

Т^*

Рисунок 6 – Граф G, его лес Т и КО-лес Т^*

Рангом графа G, имеющего n вершин и состоящего из к компонент, называется число r(G)=n-k.

Цикломатическим числом графа G называется число

(G)=m-n+k.

Если множество вершин графа G(X,A) есть Х=Х₁Х₂, причем Х₁Х₂=, то множество всех ребер графа G, имеющих одну концевую вершину в Х₁, а другую в Х₂, называется разрезом графа G.

Эйлеровым путем (циклом) графа G называется путь (цикл), содержащий все ребра графа ровно один раз.

Граф G, обладающий эйлеровым циклом, называется эйлеровым графом.

Граф G является эйлеровым тогда и только тогда, когда граф G является связным, и все его вершины имеют четную степень.

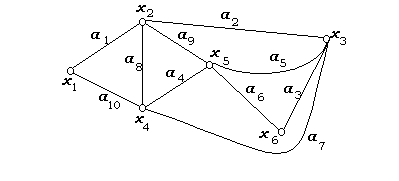Граф G обладает эйлеровым путем с концами x, y тогда и только тогда, когда он является связным, и x, y – единственные его вершины нечетной степени (рисунок 7).

а)

б) в)

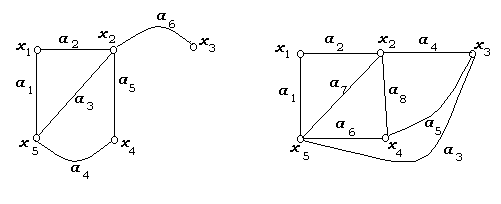
Рисунок 7 – а) Эйлеров граф;

б) Граф, обладающий эйлеровым

путем;

в) Гамильтонов граф

Гамильтоновым путем (циклом) графа G называется путь (цикл), проходящий через каждую вершину графа G только по одному разу.

Граф, обладающий гамильтоновым циклом, называется гамильтоновым.

Достаточным условием существования гамильтонова цикла является полнота графа G.

Рассмотрим орграф или граф G с n вершинами и m дугами (ребрами).

Матрица смежности А=а_ij_nn орграфа (графа) G - это матрица, элементы которой определяются из условия:

Матрица инциденций В=b_ij_nm орграфа G - это матрица, строки которой соответствуют вершинам, а столбцы ребрам графа; элементы матрицы определяются следующим образом:

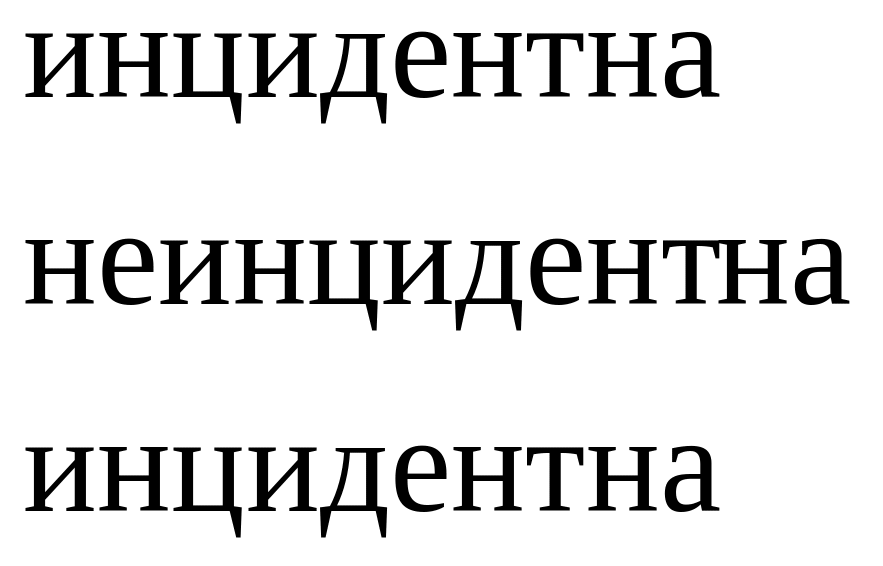
В матрице инциденций неориентированного графа b_ij равно 1 или 0 в зависимости от того, инцидентно j-тое ребро i-той вершине графа или нет.

Матрица сильной связности S={s_ij}_nn орграфа G – это матрица, элементы которой определяются так:

При этом считается, что вершина x_j достижима из x_i, если либо x_j=x_i, либо существует путь, соединяющий х_i с x_j.

Орграф, каждая вершина которого достижима из любой другой, называется сильно связным.

Потоком f(x,y) (или f(a)) в графе называется количество однородных объектов, пересылаемых из одной вершины x графа в другую y по его дуге a=(x,y).

Пропускной способностью C(x,y) (или C(a)) дуги а называется максимальный возможный поток дуги а.

Дивергенцией потока f в вершине х называется разность между выходящими и входящими потоками этой вершины:

где

А(х) – множество дуг, выходящих из вершины х;

В(х) – множество дуг, входящих в вершину х.

Если div_f(x)0, то вершина х называется источником потока f.

Если div_f(x)0, то вершина х называется стоком потока f.

Очевидно, что .