
- •Дискретная математика
- •Введение
- •1 Теоретические вопросы
- •1 Основы теории множеств
- •1.1 Основные понятия и операции
- •1.2 Примеры
- •1.3 Варианты задачи №1
- •1.4 Варианты задачи №2
- •2 Отношения
- •2.1 Основные понятия и формулы
- •2.2 Примеры
- •2.3 Варианты задачи №3
- •3 Основы комбинаторики
- •3.1 Основные формулы
- •Примеры
- •3.3 Варианты задачи №4
- •3.4 Варианты задачи №5
- •Элементы математической логики
- •4.1 Основные понятия и формулы
- •Примеры
- •4.3 Варианты задачи №6
- •4.4 Варианты задачи №7
- •4.5 Варианты задачи №8
- •Основы теории графов
- •Основные понятия и формулы
- •5.2 Примеры
- •Варианты задачи №9
- •5.4 Нахождение кратчайших путей
- •5.5 Варианты задачи №10
- •Сетевое планирование
- •Основные понятия и формулы
- •Примеры
- •Варианты задачи №11
- •Содержание
1.2 Примеры
Пример 1. А – множество делителей числа 15; В – множество простых чисел, меньших 10; С - множество четных чисел, меньших 9. Описать каждое множество перечислением. Найти: АВ, АС, ВС,
(АС)В, АВС.
Решение
Исходя из условия находим А=1;3;5;15,B=2;3;5;7, C=2;4;6;8. Тогда AB=1;2;3;5;7;15, BC=2, AC=, AC=1;2;3;4;5;6;8;15, (AC)B=2;3;5, ABC=.
Пример 2. В группе из 100 туристов 70 человек знают английский язык, 45 – французский, 25 человек знают оба языка. Сколько туристов не знают ни английского, ни французского языка?
Решение
Пусть A – множество туристов, знающих английский язык, F – французский. По условию А=70, F=45, количество туристов, знающих оба языка, равно AF=25. Множество туристов, знающих хотя бы один язык – это следующее AF. Тогда по формуле находим AF=A+F-AF=70+45-25=90. Так как всего туристов 100, а из них знают хотя бы один язык 90, то не знают ни английского, ни французского языка 100-90=10 туристов.
1.3 Варианты задачи №1
Найти
![]() для
вариантов 1 – 10.
для
вариантов 1 – 10.
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
Изобразить на координатной плоскости
множества
![]() для вариантов 11 – 26.
для вариантов 11 – 26.
Условие, которому удовлетворяют координаты точек, принадлежащих множеству |
||
|
А |
В |
11. |
|
|
12. |
|
|
13. |
|
|
14. |
|
|
15. |
|
|
16. |
|
|
17. |
|
|
18. |
|
|
19. |
|
|
20. |
|
|
21. |
|
|
22. |
|
|
23. |
|
|
24. |
|
|
25. |
|
|
26. |
|
|
Найти
![]() для
вариантов 27 – 30.
для
вариантов 27 – 30.
U – множество целых чисел, A – множество четных чисел, B – множество чисел, которые кратны 4.
U – множество натуральных чисел, A – множество нечетных чисел, B – множество корней уравнения
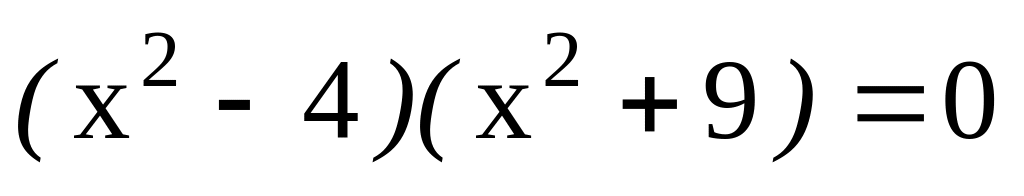 .
.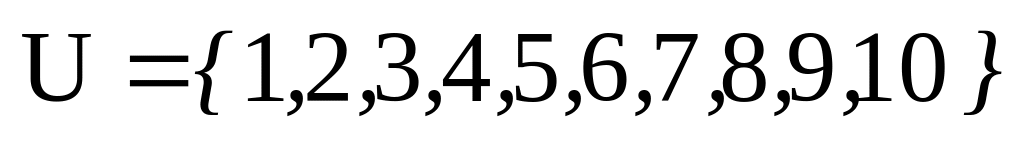 ,
А – множество простых чисел, В –
множество корней уравнения
,
А – множество простых чисел, В –
множество корней уравнения
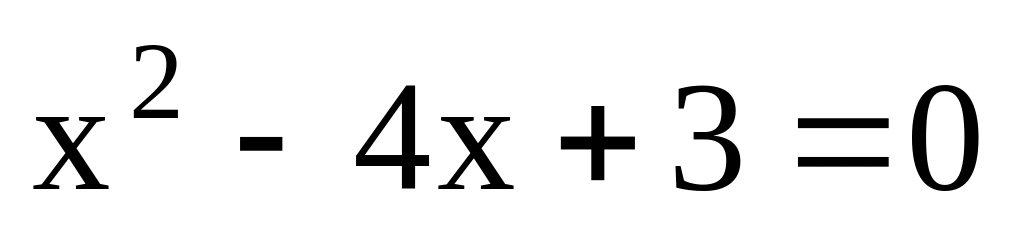 .
., А – множество составных чисел, В – множество степеней числа 2.
1.4 Варианты задачи №2
Доказать тождества
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
11.
![]() .
.
12.
![]() .
.
13.
![]() .
.
14.
![]() .
.
15.
![]() .
.
Доказать, что
16.
![]() .
.
17.
![]() .
.
18.
![]() .
.
19.
![]() .
.
20.
![]() .
.
21.
![]() .
.
22.
![]() .
.
23.
![]() .
.
24.
![]() .
.
25.
![]() .
.
26.
![]() .
.
27.
![]() .
.
28.
![]() .
.
29.
![]() .
.
30.
![]() .
.
2 Отношения
2.1 Основные понятия и формулы
Если а и b – объекты, то через (а, b) обозначим упорядоченную пару. Равенство упорядоченных пар определяется следующим образом:
(a, b)=(c, d) тогда и только тогда, когда a=b и c=d.
Прямым (декартовым) произведением множеств А и В называется множество упорядоченных пар
А![]() В
={(a , b):
a
В
={(a , b):
a![]() A,
b
B}.
A,
b
B}.
Аналогично определяется упорядоченная n-ка эелементов и декартово произведение n множеств.
n-ой степенью
множества А называется его прямое
n-кратное произведение
на себя и обозначается так:
![]() .
.
Бинарным отношением между элементами множеств A и B называется любое подмножество R множества А B. Если А=B, то отношение называется бинарным отношением на A. Вместо (x,y) R часто пишут xRy.
Областью определения бинарного отношения R называется множество
![]() =
{x: существует y
такое, что (x,y)
R}.
=
{x: существует y
такое, что (x,y)
R}.
Областью значений бинарного отношения R называется множество
![]() = {y: существует x
такое, что (x,y)
R}.
= {y: существует x
такое, что (x,y)
R}.
Для бинарных отношений определены обычным образом теоретико-множественные операции объединения, пересечения и т.д.
Дополнением бинарного отношения R
между элементами A и B
называется отношение
![]() =(A
B)
\ R.
=(A
B)
\ R.
Обратным отношением для бинарного отношения R называется отношение R -1={(x,y): (y,x) R}.
Композицией (произведением) отношений
R1 и R2
называется отношение R1![]() Rn
={(x,y):
существует z такое, что
(x,z)
R1
и (z,y)
R2}.
Rn
={(x,y):
существует z такое, что
(x,z)
R1
и (z,y)
R2}.
Пусть
![]() и множество A состоит из
n элементов, пронумеруем
их. Тогда элементы бинарного отношения
R можно представить
матрицей ||R|| порядка n
и множество A состоит из
n элементов, пронумеруем
их. Тогда элементы бинарного отношения
R можно представить
матрицей ||R|| порядка n![]() n
такой, что ее элементы rij
находятся из условия:
n
такой, что ее элементы rij
находятся из условия:
![]()
![]()
![]()
Элементы rij
матрицы ||R|| композиции
отношений P и S,
т.е.
![]() ,
определяются следующим образом:
,
определяются следующим образом:
![]() .
.
Здесь
![]() и
и
![]() - логические операции: дизъюнкция и
конъюнкция соответственно.
- логические операции: дизъюнкция и
конъюнкция соответственно.
Бинарное отношение R на множестве A называется рефлексивным, если
(x, x) R для всех x A,
иррефлексивным (антирефлексивным), если
(x, x)![]() R
для всех x
A.
R
для всех x
A.
Бинарное отношение R на множестве A называется симметричным, если для всех х, у A:
из того, что <x, y>
R,
следует <y, x>![]() R,
R,
антисимметричным, если для всех х, у A :
из того, что <x, y> R и <y, x> R, следует x=y.
Бинарное отношение R на множестве A называется транзитивным, если для всех х, у, z A:
из того, что <x, y> R и <y, z> R, следует <x, z> R.
Рефлексивное, транзитивное и симметричное отношение на множестве A называется эквивалентностью на A.
Бинарное отношение R на множестве A называется предпорядком на A, если оно рефлексивно и транзитивно. Рефлексивное, транзитивное и антисимметричное отношение на множестве A называется частичным порядком на A. Частичный порядок часто обозначается символом ≤ . Пишут: x<y, если x≤ y и x≠ y. Частичный порядок ≤ на множестве A называется линейным, если любые два элемента из A сравнимы по отношению ≤ , т.е. x≤ y или y≤ x для любых x, y A. Множество A с заданным на нем частичным (линейным) порядком ≤ называется частично (линейно) упорядоченным.
Транзитивным замыканием R+
отношения R является
объединение всех его положительных
степеней, т.е. R+=![]() .
Под n-ой степенью
отношения R понимается
его n-кратная композиция
с самим собой, т.е.
.
Под n-ой степенью
отношения R понимается
его n-кратная композиция
с самим собой, т.е.
![]() .
.
