4.11 Конструирование зубчатых колес и определение их размеров.

Конструктивные формы колес в основном определяются их диаметрами и способом соединения с валом, на который они устанавливаются.

Зубчатые колеса состоят из:

-обода колеса толщиной δ , несущего венец зубьев;

-ступицы колеса устанавливаемой на вал. Ступица колеса имеет два конструктивных размера диметр ступицы и длину ступицы ;

-диска колеса толщиной С. Диск колеса соединяет обод со ступицей.

Зубчатые цилиндрические колеса выполняют:

-кованными при малых диаметрах <200мм.

-кованными или штампованными при диаметрах до 500мм.

-литыми при больших диаметрах с диском или со спицами.

Зубчатые цилиндрические шестерни конструируют двух исполнений:

-вместе с валом(вал-шестерня)и

-отдельно от вала(насадная шестерня).

Вал-шестерню выполняют в тех случаях, когда расстояние Х (толщина) тела шестерни между впадиной зуба и пазом для шпонки t меньше установленной нормативной (допускаемой) равной [X]≤ 2.5 m_t.

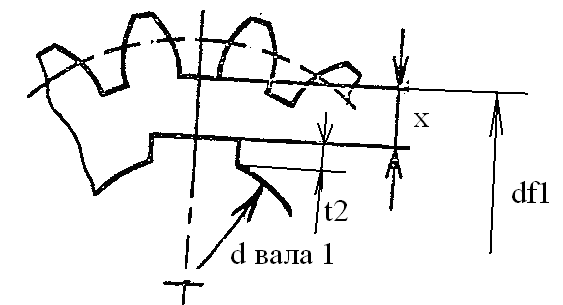
Рис. 14

Рабочая(фактическая) толщина тела Х между впадиной зуба и пазом для шпонки определяется по формуле:

и сравнивается с нормативной (допускаемой), для этой же толщины тела равной

При условии, когда X<[X] выполняется вал-шестерня, а при условии, когда X>[X] выполняется насадная шестерня (отдельно от вала)

Конструкции цилиндрических колес

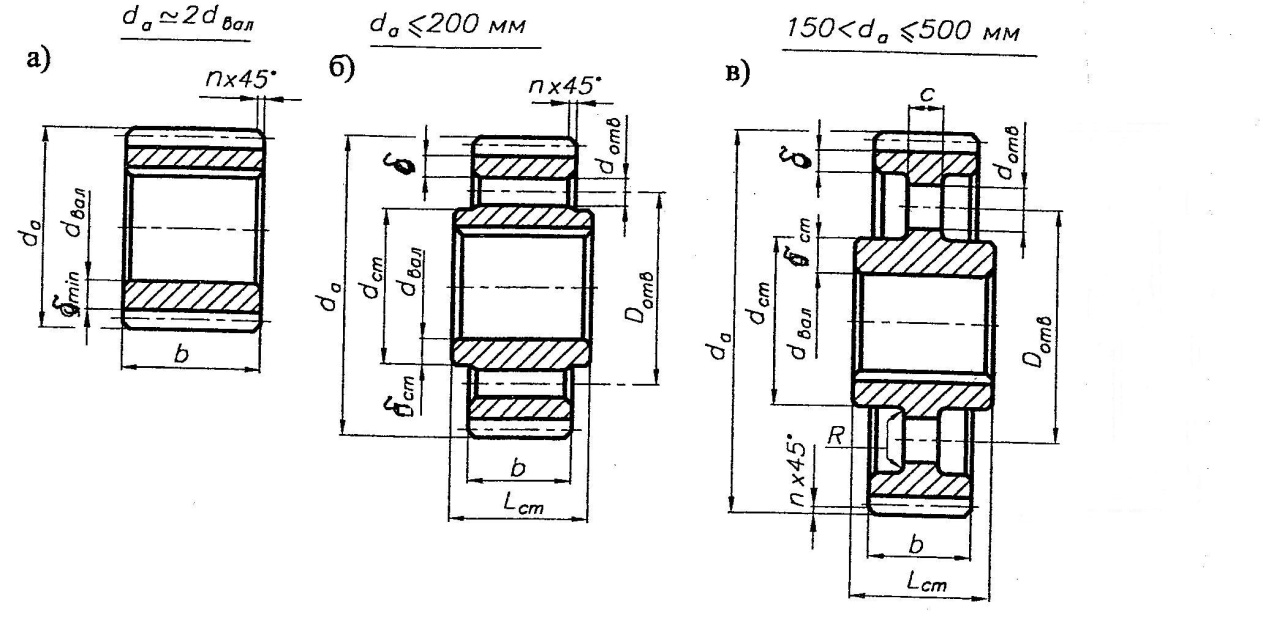
Рис. 15 Колеса кованные.

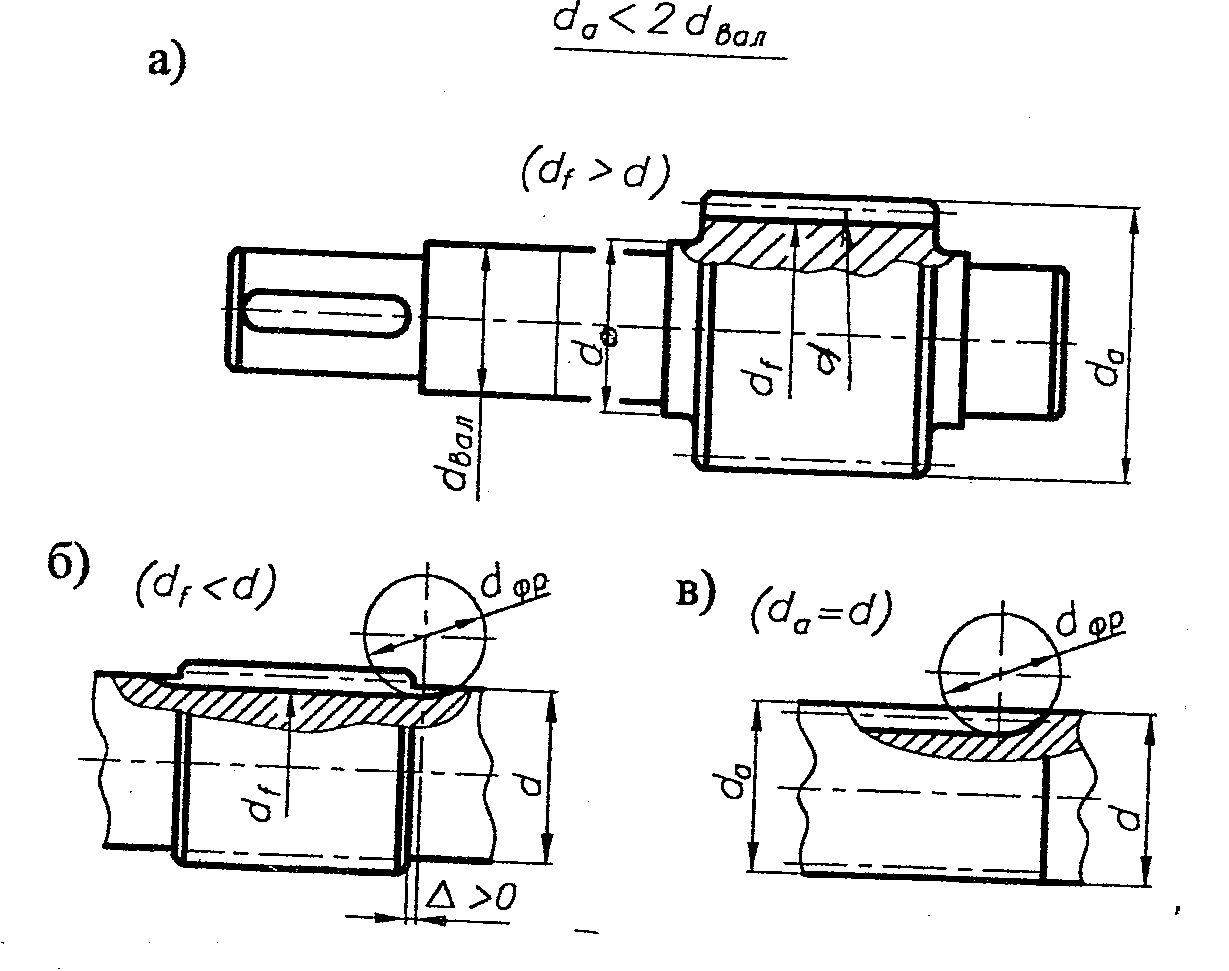
Рис 16. Вал шестерни

Определение конструктивных размеров цилиндрических колес ведут по эмпирическим формулам:

- толщина обода колеса под зубчатым венцом

δ₀ =(2,5·m_n+2)

-длина ступицы стальных колес

ι_ст =(0.8…1.5)·d_вала под зубчатым колесом

-диаметр ступицы стальных колес

d_ст =(1.5…1.7)·d_вала под зубчатым колесом

-толщина диска колеса

с =(0.15…0.3) · В₂

диаметр центровой окружности

D_отв=0.5(d_а+d_ст)

-диаметр отверстий

d_отв=0.25(d_а-d_ст)

4.12 Cилы, нагружающие валы цилиндрического редуктора.

Выявим силовые компоненты в проектируемых цилиндрических редукторах. Для этого мысленно разделим колеса передачи и покажем нагрузки на каждое звено отдельно.

Анализ сил действующих в зацеплении зубьев показывает, что силовые компоненты равны между собой, но противоположны по направлению.

Момент вращения ведущего вала Т₁ является моментом движущих сил, его направление совпадает с направлением вращения вала ω₁, а направление окружной силы Ft₁ (как реакции) всегда противоположно направлению вращению вала ω₁, F_t действует по касательной к делительной окружности.

Момент вращения ведомого вала Т₂ является моментом сил сопротивления, поэтому его направление противоположно направлению вращения вала ω₂ , а направление окружной силы Ft₂ всегда совпадает с направлением вращения вала ω₂; действует по касательной к делительной окружности.

Радиальные силы F_r1 и F_r2 всегда направлены к центрам зубчатых колес, основание III закон Ньютона.

При определении направлений осевых усилий учитывают направление вращения колёс ω и направление линий наклона зуба β ( правое или левое). Для передач редукторов предпочтительно направление линий зуба: шестерни - левое, колеса – правое. Векторы осевых сил всегда параллельны осям валов.

Эти направления осевых сил F_a и конструкции опор должны быть подобраны так, чтобы осевая сила F_a воспринималась бы подшипником, нагруженным меньшей радиальной суммарной реакцией F_r^∑

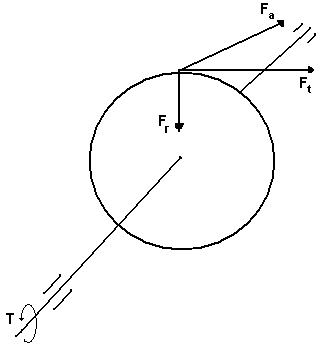
Рис. 17 Схема сил, нагружающих валы цилиндрического редуктора

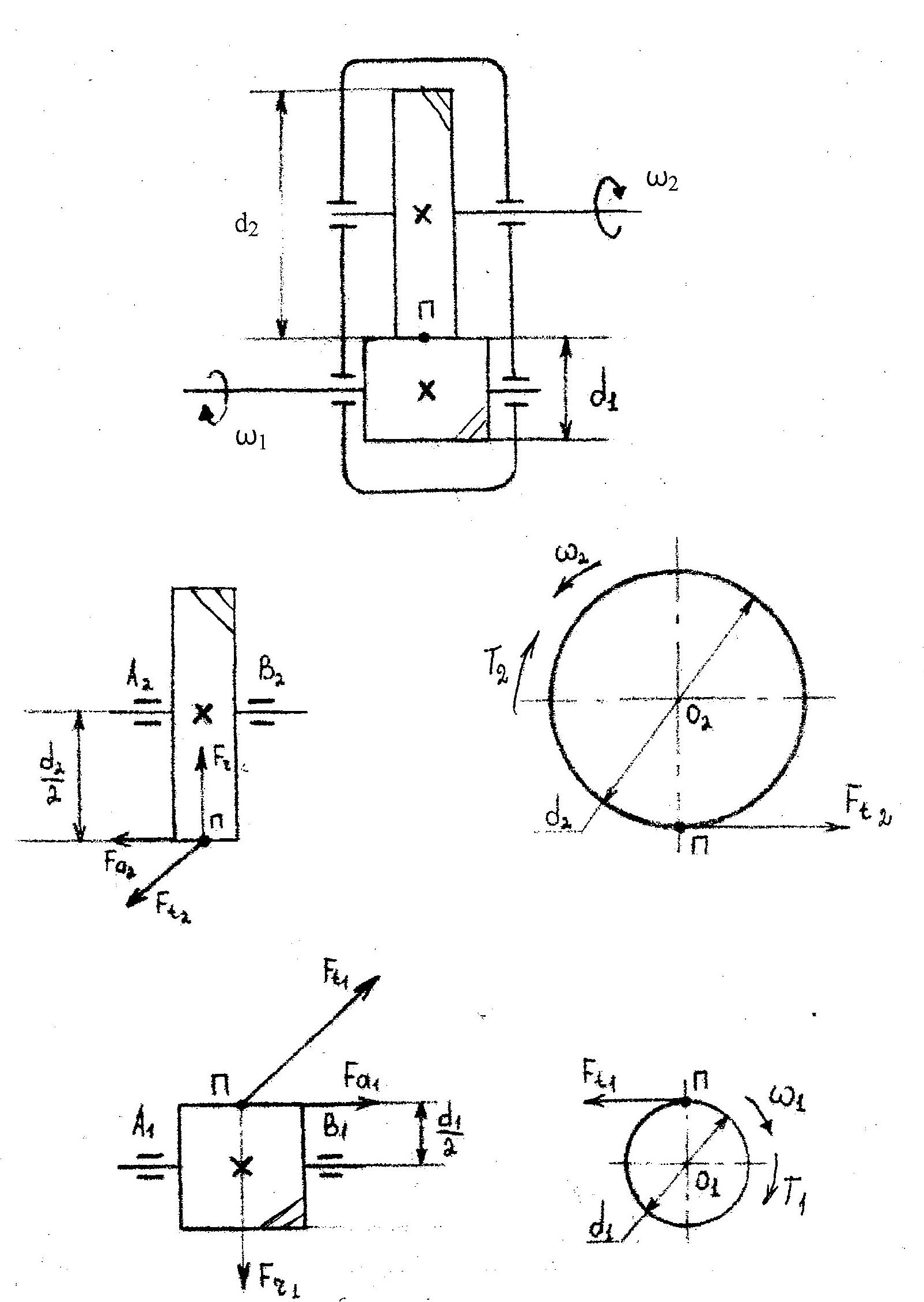
Рис.18 Схема усилий, действующих на валы редуктора.

Составляющие силы в зацеплении цилиндрической косозубой передачи определяют по формулам:

- окружную силу ;

- радиальную силу ;

- осевую силу .

где Т – вращающий момент передаваемый зубчатым колесом;

d - диаметр делительной окружности;

α_w = 20° - угол зацепления нормального колеса;

β = (8°…15°) – угол наклона линии колеса;

β = 0 – для прямозубых цилиндрических колес.

Выявим виды деформаций в общем случае нагружения проектируемых редукторных валов.

Известно, что с помощью метода сечений мы внутренние силовые факторы уравновешиваем внешними силами приложенными к отсеченной части тела, т.е. находим статический эквивалент системы внутренних сил – главный вектор и главный момент. Каждый из них как главный вектор так и главный момент может быть представлен тремя составляющими (тремя компонентами). Конструкции под действием приложенных к ним сил деформируются.

В общем случае нагружения в поперечном сечении вала возникает шесть внутренних силовых факторов, каждому из них сопутствует определенный вид деформации.

Будем считать, что ось X есть продольная ось вала. Оси Z и Y – оси поперечного сечения вала (главные центральные оси поперечного сечения вала).

Направление вращения валов редуктора будем определять по направлению вращения двигателя. Условимся момент пары сил обозначать буквой m.

Для одноступенчатого цилиндрического косозубого редуктора;

Радиальная сила F_r вызывает следующие деформации:

- изгиб вала в вертикальной плоскости YПZ, создавая момент силы относительно оси Z,

и одновременно вызывает сдвиг частиц поперечного сечения вала вдоль оси Y силой Q_y = F_r .

Осевая сила F_α вызывает следующие деформации:

- изгибает вал в вертикальной плоскости YПZ, создавая пару сил с моментом относительно оси Z,

и вызывает сжатие (растяжение) вала силой

Окружная сила F_t вызывает следующие деформации:

- изгиб вала в горизонтальной плоскости XПZ, создавая моменты силы относительно оси У, М_у=M_Ft=M_изг и одновременно

- крутит вал относительно оси X, создавая пару сил с моментом m,

- вызывает сдвиг частиц поперечно сечения вала вдоль оси Z силой Q_z=F_t

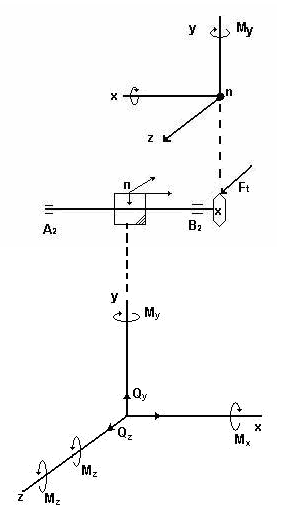
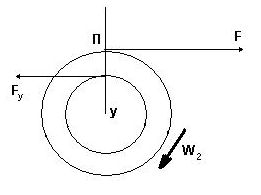
Рис. 19