9.3. Средний арифметический и средний гармонический индексы, тождественные агрегатному

Наряду с агрегатными общие индексы могут быть построены как средние взвешенные из индивидуальных, тождественных агрегатным.

Предположим, что необходимо рассчитать агрегатный индекс цен по формуле Паше (формула 6 с отчетными весами: ), но неизвестны отдельные значения p₁ и q_1, а дано их произведение p₁q₁ (товарооборот текущего периода) и известны индивидуальные индексы цен .

Как это сделать?

Из формулы определяем , подставляем его в знаменатель агрегатной формулы:

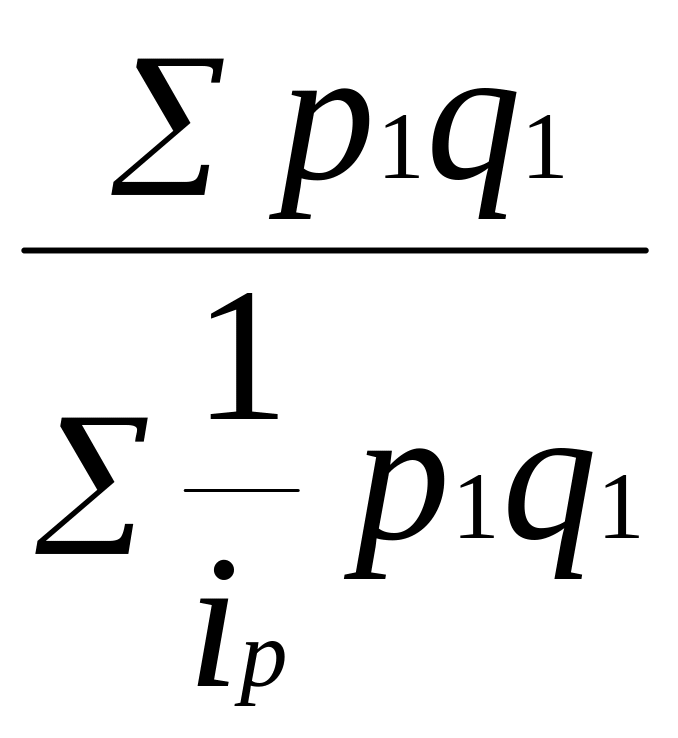I_p =  I_p = (8)

В результате получили средний гармонический индекс цен, тождественный агрегатному индексу Пааше.

Весами индивидуальных индексов в этом индексе служит стоимость отдельных видов продукции отчетного периода в ценах этого же периода p₁q_1.

Предположим нам необходимо построить агрегатный индекс цен Ласпейреса ( формула 5 с базисными весами: ). Нам не известны значения и , но известно их произведение , а так же индивидуальные индексы цен . Из индивидуального индекса цен выразим цены отчетного периода и подставим в числитель агрегатного индекса цен

, (9)

В результате получили средний арифметический индекс цен тождественный агрегатному индексу цен Ласпейреса. Весами осредняемых индивидуальных индексов в этом индексе служит объем товарооборота в базисном периоде .

Агрегатные индексы физического объема можно выразить так же через индивидуальные индексы: тождественный агрегатному индексу Паше как средней гармонический и тождественный агрегатному индексу Ласпейреса как средний арифметический.

Например, если неизвестны значения и , но известно их произведение , а так же индивидуальные индексы физического объема . Из индивидуального индекса физического объема выразим объемы отчетного периода i_q = - подставляем в агрегатный индекс

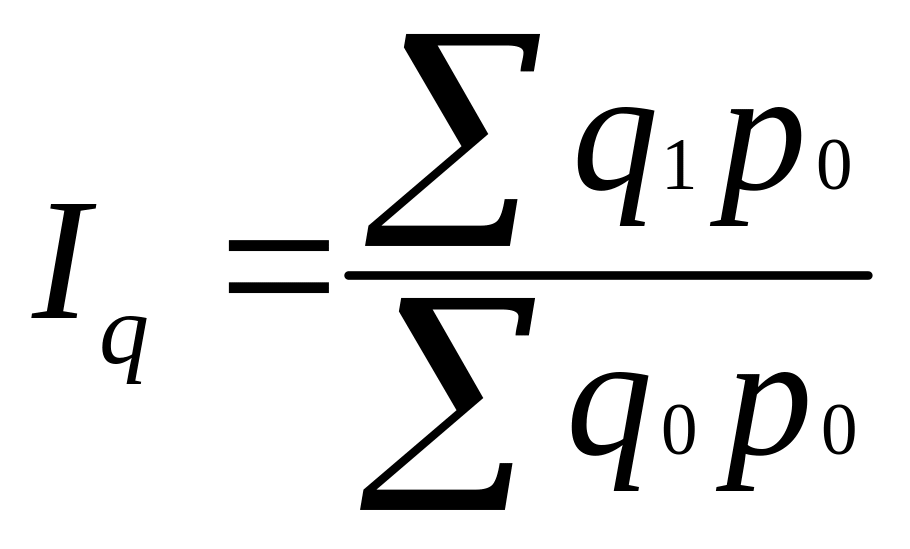
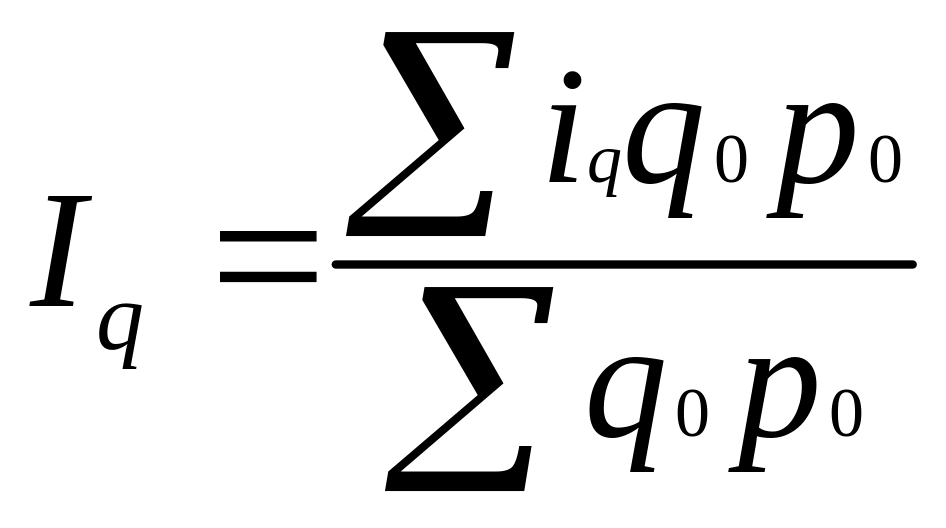 (10)

В результате получили средний арифметический индекс физического объема, тождественный агрегатному индексу Ласпейреса.

При выборе весов следует иметь в виду, что средний индекс должен быть тождественен агрегатному, который является основной формой индекса. Учитывая, что соотношение характеризует долю данного вида продукции в общей стоимости продукции базисного периода , средний арифметический индекс физического объема (10) будет иметь вид:

Например, воспользуемся данными графы 6 таблицы 1 и графы 2 таблицы 2 для расчета среднего арифметического индекса физического объема продукции:

Получим такой же результат, как и при расчете агрегатного индекса физического объема по формуле Ласпейреса.

Допустим, что имеются данные о динамике объема выпуска каждого вида продукции и стоимости каждого вида продукции в отчетном периоде , тогда индекс физического объема можно получить путем суммирования величин , а знаменатель – путем деления фактической стоимости каждого вида продукции на соответствующий индивидуальный индекс физического объема продукции, то есть путем деления:

,

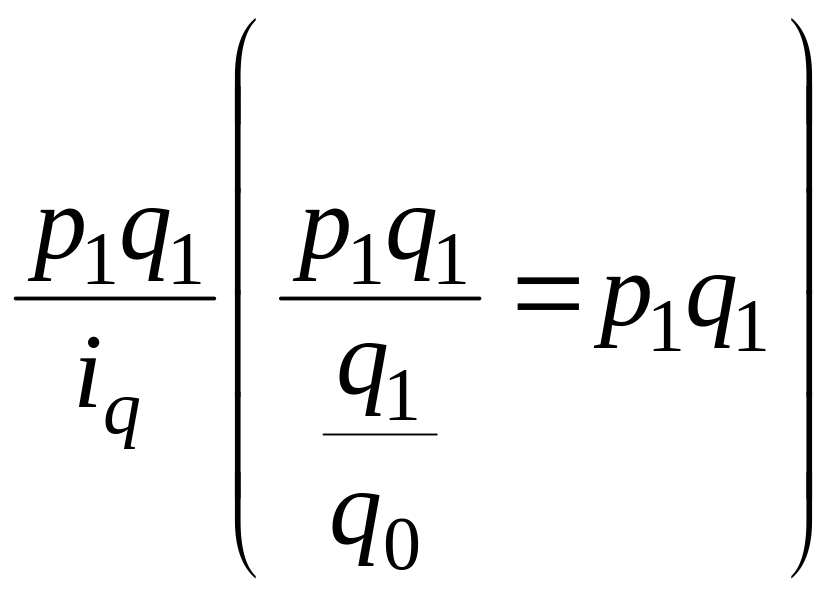тогда (11).

Таким образом, в этом случае расчет выполняется по формуле среднего взвешенного гармонического индекса физического объема тождественного агрегатному индексу Пааше.

Например, используем графы 6 таблицы 1 и графы 3 таблицы 2:

.

Получен такой же результат, как и при расчете агрегатного индекса по формуле Пааше.

Из сказанного следует, что применение той или иной формулы индекса физического объема (агрегатного, среднего арифметического или среднего гармонического) зависит от имеющейся в нашем распоряжении информации.

.

Рассмотрение методологии исчисления индексов и их применения в экономическом анализе сказать, что важной особенностью общих индексов, построение и расчет которых составляет суть индексного метода, является то, что они обладают синтетическими и аналитическими свойствами. Синтетические свойства общих индексов состоят в том, что они выражают относительные изменения сложных (разнотоварных) явлений, отдельные части и элементы которых непосредственно несоизмеримы.

Аналитические свойства общих индексов говорят о том, что посредством индексного метода определяется влияние факторов на изменение изучаемого показателя.