§ 2. Вектор поляризации р

Продолжив наш анализ, мы обнаружим, что идея о проводя­щих и непроводящих участках не так уж существенна. Любой из маленьких шариков действует как диполь, момент которого создается внешним полем. Для понимания диэлектриков суще­ственной является идея о том, что в материале возбуждается множество маленьких диполей. Почему они возбуждаются — то ли потому, что в материале есть проводящие шарики, то ли по каким-либо другим причинам — абсолютно несуще­ственно.

Почему поле должно индуцировать дипольный момент у ато­ма, хотя атом не является проводящим шариком? Мы обсудим этот вопрос гораздо подробнее в следующей главе, которая бу­дет посвящена внутреннему механизму диэлектрических мате­риалов. А сейчас мы дадим лишь один пример, только чтобы проиллюстрировать возможный механизм. Атом имеет ядро с по­ложительным зарядом, окруженное отрицательными электрона­ми. В электрическом поле ядро притягивается в одну сторону, а электроны в другую. Орбиты или плотности вероятности элект­ронов (или какая-либо другая картина, используемая в кванто­вой механике) несколько искажаются (фиг. 10.4); центр тяжести отрицательных зарядов сместится и больше не будет совпадать с положительным зарядом ядра. Мы уже обсуждали такое рас­пределение заряда. Если взглянуть на него издалека, то подоб­ная нейтральная конфигурация в первом приближении эквива­лентна маленькому диполю.

Если поле не чересчур велико, естественно считать величину индуцированного дипольного момента пропорциональной полю. Иначе говоря, небольшое поле сместит заряды чуть-чуть, а более сильное поле раздвинет их дальше — пропорционально величине поля, пока смещение не станет чересчур большим.

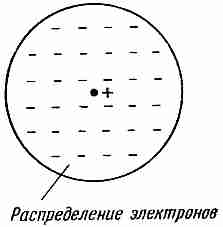
Фиг. 10.4. Распределение электронов атома в электрическом поле сдвигается относительно ядра.

До конца этой главы мы будем считать, что дипольный мо­мент в точности пропорцио­нален полю.

Предположим теперь, что в каждом атоме заряды q раз­делены промежутком , так что q есть дипольный момент одного атома. (Мы пишем , потому что d уже использовано для обозначения расстояния между пластинами.) Если в еди­нице объема имеется N атомов, то дипольный момент в еди­нице объема равен Nq. Этот дипольный момент в единице объема мы запишем в виде вектора Р. Нет необходимости подчеркивать, что он лежит в направлении всех отдельных дипольных моментов, т. е. в направлении смещения за­рядов :

(10.4)

Вообще говоря, Р будет меняться в диэлектрике от точки к точке. Но в каждой точке Р пропорционален электрическому полю Е. Константа пропорциональности, которая определяется тем, насколько легко можно сместить электрон, зависит от сорта атомов в материале.

О том, что действительно определяет поведение этой констан­ты и степень ее постоянства для больших полей, а также о том, что происходит внутри разных материалов, мы поговорим позже. А пока мы просто предположим, что существует какой-то механизм, благодаря которому индуцируется дипольный момент, пропорциональный электрическому полю.