§ 5. Электростатическое поле сетки

Напоследок мы хотим изложить еще одно интересное свой­ство электрических полей. Оно используется в электрических приборах, электронных лампах и для других целей. Речь идет о поведении электрического поля близ сетки, составленной из заряженных проволочек. Чтоб упростить задачу, возьмем плос­кую систему параллельных проволочек бесконечной длины, про­межутки между которыми одинаковы.

Если мы посмотрим на поле где-то высоко над плоскостью проволочек, перед нами предстанет однородное электрическое поле, такое, словно заряд распределен на плоскости равномер­но. По мере приближения к сетке начнутся отклонения от преж­ней однородности. Мы хотим оценить, насколько близко от сетки появятся заметные изменения в потенциале.

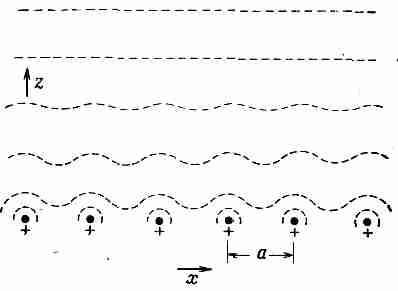
Фиг. 7.8. Эквипотен­циальные поверхности над однородной сеткой из заряженных прово­лочек.

На фиг. 7.8 показа­но примерное расположение эквипотенциальных поверхностей на разных расстояниях от сетки. Чем ближе к сетке, тем сильнее колебания. Двигаясь параллельно сетке, мы заметим, что поле изменяется периодически.

Мы уже знаем (см. вып. 4, гл. 50), что любая периодическая величина может быть представлена в виде суммы синусных волн (теорема Фурье). Посмотрим, нельзя ли найти подходящую коле­бательную функцию, которая удовлетворяет нашим уравнениям поля.

Е сли проволочки лежат в плоскости ху параллельно оси y, то можно попробовать испытать члены вида

(7.41)

г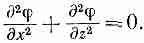 де а — расстояние между нитями, а n — число колебаний. (Мы предположили, что нити эти очень длинные, так что ника­ких изменений по у не заметно.) Полное решение должно со­стоять из суммы таких членов при n=1, 2, 3... Чтоб получился правильный потенциал, оно должно в области над сеткой (где зарядов нет) подчиняться уравнению Лапласа, т. е.

Испытывая этим уравнением функцию  из (7.41), мы получаем

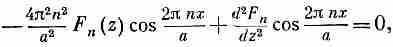
(7.42)

т.е. F_n(z) должно удовлетворять условию

(7.43)

И так, должно быть

(7.44)

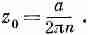
(7.45)

Мы обнаружили, что если имеется компонента Фурье n-й гар­моники поля, то эта компонента должна убывать по экспоненте с высотой, причем характерным расстоянием является z₀=a/2n. Амплитуда у первой гармоники (n=1) уменьшается в е^2 раз (очень резкое падение) каждый раз, когда мы удаляемся от сетки на величину одного промежутка а. Другие гармоники убы­вают еще быстрее. Мы видим, что уже на расстоянии в несколько а сетка кажется почти однородной, т. е. колебания поля очень малы. Конечно, всегда остается «нулевая гармоника» поля

₀=-E₀z.

которая и дает однородное поле при больших z. Для полного решения нужно добавить этот член к сумме членов вида (7.41) с F_n из (7.44) , причем каждый член надо взять с коэффициентом А_n . Эти коэффициенты выбираются так, чтобы после дифферен­цирования получилось поле, согласующееся с плотностью заря­дов К на проволочках сетки.

Развитым нами методом можно объяснить, почему электро­статическая защита с помощью сетки ничуть не хуже сплошных листов металла. Поле за сеткой равно нулю всюду, за исключе­нием промежутка у самой сетки, не превышающего по размерам нескольких ее ячеек. Мы видим, что медная сетка, которая на­много легче и дешевле сплошной медной обшивки, вполне при­годна для защиты чувствительного электрического оборудова­ния от возмущающих внешних полей.

* О новых работах по этому вопросу и библиографию см. в статье С. J.Powell, J.B. Swann, Phys. Rev., 115, 869 (1959).

Глава 8

ЭЛЕКТРОСТАТИЧЕСКАЯ ЭНЕРГИЯ

§1 .Электростатиче­ская энергия зарядов. Однородный шар

§2.Энергия конденсатора. Силы, действующие на заряженные проводники

§З.Электростатическая энергия ионного кристалла

§4.Электростатиче­ская энергия ядра

§5,Энергия в электро­статическом поле

§6.Энергия точечного заряда

Повторить: гл. 4 (вып. 1) «Сохранение энергии»; гл. 13 и 14 (вып. 1) «Работа и потенциальная энергия»

§ 1. Электростатическая энергия зарядов. Однородный шар

Одно из самых интересных и полезных от­крытий в механике —это закон сохранения энер­гии. Зная формулы для кинетической и потен­циальной энергий механической системы, мы способны обнаруживать связь между состоя­ниями системы в два разных момента времени, не вникая в подробности того, что происходит между этими моментами. Мы хотим определить теперь энергию электростатических систем. В электричестве сохранение энергии окажется столь же полезным для обнаружения многих любопытных фактов.

Закон, по которому меняется энергия при электростатическом взаимодействии, очень прост; на самом деле мы его уже обсуждали. Пусть имеются заряды q₁ и q₂, разделенные про­межутком r₁₂. У этой системы есть какая-то энергия, потому что понадобилась какая-то работа, чтобы сблизить заряды. Мы подсчиты­вали работу, производимую при сближении двух зарядов с большого расстояния; она равна

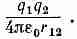
(8.1)

Мы знаем из принципа наложения, что если зарядов много, то общая сила, действующая на любой из зарядов, равна сумме сил, дей­ствующих со стороны всех прочих зарядов. От­сюда следует, что полная энергия системы не­скольких зарядов есть сумма членов, выражаю­щих взаимодействие каждой пары зарядов по отдельности. Если q_i и q_j- — какие-то два из зарядов, а расстояние между ними r_ij (фиг. 8.1),

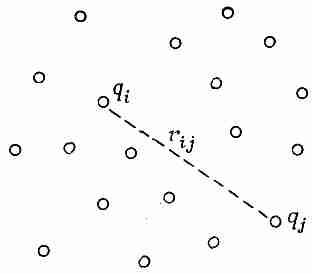
Фиг. 8.1. Электростатическая анергия системы частиц есть сумма электростатических энер­гий каждой пары.

то энергия именно этой пары равна

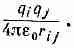
(8.2)

П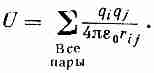 олная электростатическая энергия U есть сумма энергий все­возможных пар зарядов:

(8.3)

Если распределение задается плотностью заряда , то сумму в (8.3) нужно, конечно, заменить интегралом.

Мы расскажем здесь об энергии с двух точек зрения. Пер­вая — применение понятия энергии к электростатическим зада­чам; вторая — разные способы оценки величины энергии. По­рой легче бывает подсчитать выполненную в каком-то случае работу, чем оценить величину суммы в (8.3) или величину со­ответствующего интеграла. Для образца подсчитаем энергию, необходимую для того, чтобы собрать из зарядов однородно за­ряженный шар. Энергия здесь есть не что иное, как работа, которая затрачивается на собирание зарядов из бесконечности.

Представьте, что мы сооружаем шар, наслаивая последова­тельно друг на друга сферические слои бесконечно малой тол­щины. На каждой стадии процесса мы собираем небольшое ко­личество электричества и размещаем его тонким слоем от r до r+dr. Мы продолжаем процесс этот до тех пор, пока не добе­ремся до заданного радиуса а (фиг. 8.2). Если Q_r -— это заряд шара в тот момент, когда шар доведен до радиуса r, то работа, требуемая для доставки на шар заряда dQ, равна

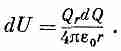
(8.4)

Фиг. 8.2. Энергию однород­но заряженного шара можно рассчитать, вообразив, что его слепили, последовательно наслаивая друг на друга сферические слои.

Е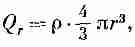 сли плотность заряда внутри шара есть , то заряд Q_r равен

Уравнение (8.4) превращается в

(8.5)

Полная энергия, требуемая на то, чтобы накопить полный шар зарядов, равна интегралу по dU от r=0 до r=а, т.е.

(8.6)

а если мы желаем выразить результат через полный заряд Q шара, то

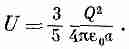
(8.7)

Энергия пропорциональна квадрату полного заряда и об­ратно пропорциональна радиусу. Можно представить (8.7) и так: среднее значение (1/r_ij) по всем парам точек внутри шара равно ⁶/₅а.