§ 2. Поток векторного поля

Прежде чем рассматривать следующую интегральную теоре­му — теорему о дивергенции,— хотелось бы разобраться в од­ной идее, смысл которой в случае теплового потока легко усваи­вается. Мы уже определили вектор h, представляющий коли­чество тепла, протекающего сквозь единицу площади в еди­ницу времени. Положим, что внутри тела имеется замкнутая поверхность S, ограничивающая объем V (фиг. 3.3). Нам хочется узнать, сколько тепла вытекает из этого объема. Мы это можем, конечно, определить, рассчитав общий тепловой поток через поверхность S.

Обозначим через da площадь элемента поверхности. Этот символ заменяет двумерный дифференциал. Если, например, элемент окажется в плоскости ху, то

da = dxdy.

Позже мы будем иметь дело с интегралами по объему, и тогда будет удобно рассматривать элемент объема в виде малого куби­ка и обозначать его dV, подразумевая, что

dV= dxdydz.

Кое-кто пишет и d²a вместо da, чтобы напомнить самому себе, что это выражение второй степени; вместо dV пишут также d³V. Мы будем пользоваться более простыми обозначениями, а вы уж постарайтесь не забывать, что у площадей бывают два измерения, у объемов — три.

Ф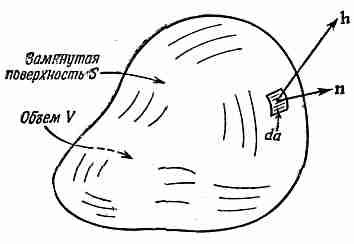 иг. 3.3. Замкнутая поверх­ность S, ограничивающая объем V.

Единичный вектор n — внешняя нор­маль к элементу поверхности da, a h — вектор теплового потопа сквозь элемент поверхности.

Поток тепла через элемент поверхности da равен произведе­нию площади на составляющую h, перпендикулярную к da. Мы уже определяли n — единичный вектор, направленный наружу перпендикулярно к поверхности (см. фиг. 3.3). Искомая составляющая h равна

h_n=h•n, (3.9)

и тогда поток тепла сквозь da равен

h•nda. (3.10)

А весь поток тепла через произвольную поверхность получается суммированием вкладов от всех элементов поверхности. Иными словами, (3.10) интегрируется по всей поверхности

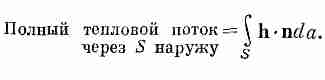
(3.11)

Этот интеграл мы будем называть «поток h через поверх­ность». Мы рассматриваем h как «плотность потока» тепла, а поверхностный интеграл от h — это общий поток тепла наружу через поверхность, т. е. тепловая энергия за единицу времени (джоули в секунду).

М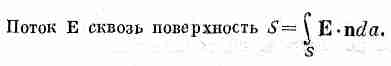 ы хотим эту идею обобщить на случай, когда вектор не представляет собой потока какой-то величины, а, скажем, является электрическим полем. Конечно, если это будет нужно, то и в этом случае все равно можно проинтегрировать нормаль­ную составляющую электрического поля по площади. Хотя теперь она уже не будет ничьим потоком, мы все еще будем упот­реблять слово

«поток». Мы будем говорить, что

(3.12)

Слову «поток» мы придаем смысл «поверхностного интеграла от нормальной составляющей» некоторого вектора. То же опре­деление будет применяться и тогда, когда поверхность незамк­нута.

А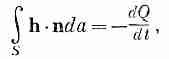 возвращаясь к частному случаю потока тепла, обратим внимание на те случаи, когда количество тепла сохраняется. Представьте себе, к примеру, материал, в котором после перво­начального подогрева не происходит ни дальнейшего подвода, ни поглощения тепла. Тогда, если из какой-то замкнутой по­верхности наружу поступает тепло, содержание тепла во внут­реннем объеме должно падать. Так что в условиях, когда количество тепла сохраняется, мы говорим, что

(3.13)

где Q — запас тепла внутри S. Поток тепла из S наружу равен со знаком минус быстроте изменения со временем общего за­паса тепла Q внутри S. Это толкование возможно оттого, что речь идет о потоке тепла, и оттого, что мы предположили, что количество тепла сохраняется. Конечно, если бы внутри объема создавалось тепло, нельзя было бы говорить о полном запасе тепла в нем.

У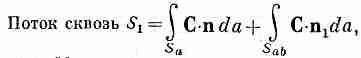 кажем теперь на интересное свойство потока любого век­тора. Можете при этом представлять себе вектор потока тепла, но верно это будет и для произвольного векторного поля С. Представьте себе замкнутую поверхность S, окружающую объем V. Разобьем теперь объем на две части каким-то «сече­нием» (фиг. 3.4). Получились два объема и две замкнутые по­верхности. Объем V₁ окружен поверхностью S₁ , составленной частью из прежней поверхности S_a и частью из «сечения» S_ab. Объем V₂ окружен поверхностью S₂, составленной из остатка прежней поверхности (S_b) и замкнутой сечением S_ab. Зададим вопрос: если мы рассчитаем поток через поверхность S_l и при­бавим к нему поток сквозь поверхность S₂, будет ли их сумма равна потоку через первоначальную поверхность? Ответ гласит: «Да». Потоки через часть S_ab , общую обеим поверхностям S₁ и S₂, в точности сократятся. Для потока вектора С из V₁ можно написать

(3.14)

а для потока из V₂:

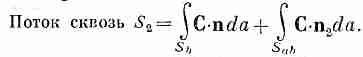
(3.15)

З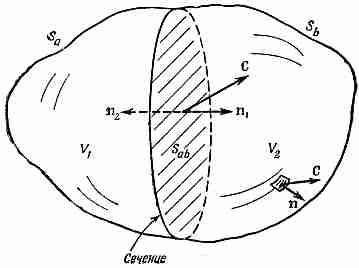 аметьте, что во втором интеграле мы обозначили внешнюю нормаль к S_ab буквой n₁, если она относится к S₁ , и буквой n₂, если она относится к S₁ (см. фиг. 3.4).

Фиг. 3.4. Объем V, заключенный внутри поверхности S, делится на две части «сече­нием» (поверхностью S_ab). Получается объем V₁, окруженный поверхностью S₁ = S_a+S_ab, и объем V₂, окруженный поверхностью S₂= S_b+S_ab.

Ясно, что n₁=-n₂, и тем с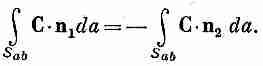 амым

(3.16)

Складывая теперь уравнения (3.14) и (3.15), мы убеждаемся, что сумма потоков сквозь S₁ и S₂ как раз равна сумме двух ин­тегралов, которые, взятые вместе, дают поток через перво­начальную поверхность S=S_a+S_b.

Мы видим, что поток через всю внешнюю поверхность S можно рассматривать как сумму потоков из тех двух частей, на которые разрезан объем. Эти части можно еще разрезать: скажем, V₁ разбить пополам. Опять придется прибегнуть к тем же доводам. Так что для любого способа разбиения первоначаль­ного объема всегда остается справедливым то свойство, что по­ток через внешнюю поверхность (первоначальный интеграл) равен сумме потоков изо всех внутренних частей.