§ 3. Колебания плазмы

Займемся теперь такими физическими задачами, в которых поле создается не закрепленными зарядами и не зарядами на проводящих поверхностях, а сочетанием обоих факторов. Ины­ми словами, полем управляют одновременно две системы урав­нений: 1) уравнения электростатики, связывающие электриче­ское поле с распределением зарядов; 2) уравнения из другой области физики, определяющие положение или движения за­рядов в поле.

Сперва мы разберем один динамический пример. В нем дви­жение зарядов контролируется законами Ньютона. Простой пример такого положения вещей наблюдается в плазме, в ионизованном газе, состоящем из ионов и свободных электронов распределенных в какой-то области пространства. Ионосфера (верхний слой атмосферы) служит примером такой плазмы. Ультрафиолетовые лучи Солнца отрывают от молекул воздуха электроны и создают свободные электроны и ионы. В плазме положительные ионы намного тяжелее электронов, так что можно пренебречь движением в ней ионов но сравнению с дви­жением электронов.

Пусть n₀ будет плотностью электронов в невозмущенном равновесном состоянии. Такой же должна быть и плотность положительных ионов, потому что в невозмущенном состоянии плазма нейтральна. Теперь допустим, что электроны каким-то образом выведены из равновесия. Что тогда получится? Если плотность электронов в какой-то области возросла, они начнут отталкиваться и стремиться вернуться в прежнее положение равновесия. Двигаясь к своим первоначальным положениям, они наберут кинетическую энергию и вместо того, чтобы заме­реть в равновесной конфигурации, проскочат мимо. Начнутся колебания. Нечто похожее наблюдается в звуковых волнах, но там возвращающей силой было давление газа. В плазме воз­вращающая сила — это действующее на электроны электриче­ское притяжение.

Чтобы упростить рассуждения, мы будем заниматься только одномерным движением электронов — скажем, в направлении x;. Предположим, что электроны, первоначально находившиеся в точке х, к моменту t сместились из положения равновесия на расстояние s (x, t). Раз они сместились, то плотность их, вообще говоря, изменилась. Это изменение подсчитать легко. Если посмотреть на фиг. 7.6, то видно, что электроны, вначале нахо­дившиеся между плоскостями а и b, сдвинулись и теперь нахо­дятся между плоскостями а' и b'. Количество электронов между а и b прежде было пропорционально n₀х; теперь то же их ко­личество находится в промежутке шириной x+s.

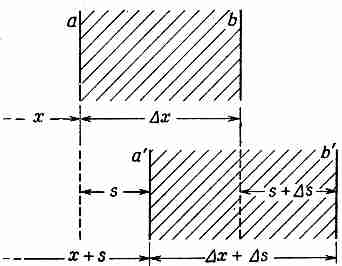
Фиг. 7.6. Движение волны в плазме.

Электроны от плоскости а сдвига­ются к а', а от b —к b'.

Плотность т еперь стала

(7.16)

Если изменение плотности мало, то можно написать [заменяя с помощью биномиального разложения (1+)^-1 на (1-)]

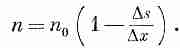
(7.17)

Ч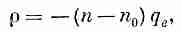 то касается ионов, то предположим, что они не сдвинулись заметно с места (инерция-то у них куда больше), так что плот­ность их осталась прежней, n₀. Заряд каждого электрона -q_e , и средняя плотность заряда в любой точке равна

или

(7.18)

(здесь s/x записано через дифференциалы).

Далее, уравнения Максвелла связывают с плотностью заря­дов электрическое поле. В частности,

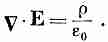
(7.19)

Если задача действительно одномерна (и никаких полей, кроме вызываемых смещением электронов, нет), то у электрического поля Е есть одна-единственная составляющая Е_х. Уравнение (7.19) вместе с (7.18) приведет к

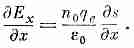
(7.20)

И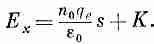 нтегрируя (7.20), получаем

(7.21)

Постоянная интегрирования К равна нулю, потому что Е_х=0 при s=0.

С ила, действующая на смещенный электрон, равна

(7.22)

т. е. возвращающая сила пропорциональна смещению s элект­рона. Это приведет к гармоническим колебаниям электронов. Уравнение движения смещенного электрона имеет вид

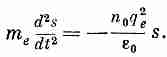
(7.23)

Отсюда следует, что s меняется по гармоническому закону. Во времени s меняется как cos t или, если использовать экспоненту (см. вып. 3), как

(7.24)

Частота колебаний _р определяется из (7.23):

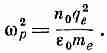
(7.25)

Это число, характеризующее плазму, называют собственной частотой колебаний плазмы, или плазменной частотой.

Оперируя с электронами, многие предпочитают получать ответы в единицах e², определяемых как

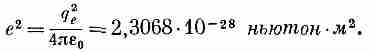
(7.26)

При этом условии (7.25) превращается в

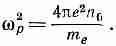
(7.27)

В таком виде эту формулу можно встретить во многих книгах.

Итак, мы обнаружили, что возмущения плазмы приводят к свободным колебаниям электронов вблизи положения равновесия с собственной частотой _р, пропорциональной корню квад­ратному из плотности электронов. Плазменные электроны ве­дут себя как резонансная система, подобная описанным в вып. 2, гл. 23.

Этот собственный резонанс плазмы приводит к интересным эффектам. Например, при прохождении радиоволн сквозь ионо­сферу обнаруживается, что они могут пройти только в том слу­чае, если их частота выше плазменной частоты. А иначе они от­ражаются обратно. Для связи с искусственным спутником мы используем высокие частоты. Если же мы хотим связаться с ра­диостанцией, расположенной где-то за горизонтом, то необхо­димы частоты меньшие, чем плазменная частота, иначе сигнал не отразится обратно к Земле.

Другой интересный пример колебаний плазмы наблюдается в металлах. В них содержится плазма из положительных ионов и свободных электронов. Плотность n₀ там очень высока, зна­чит, велика и _р. Но колебания электронов все же можно обна­ружить. Ведь, согласно квантовой механике, гармонический осциллятор с собственной частотой _р обладает уровнями энер­гии, отличающимися друг от друга на величину h_р. Значит, если, скажем, обстреливать электронами алюминиевую фольгу и очень точно измерять их энергию по ту сторону фольги, то можно ожидать, что временами электроны будут из-за колеба­ний плазмы терять как раз энергию h_p. Так это и происходит. Впервые это явление наблюдалось экспериментально в 1936 г. Электроны с энергиями от нескольких сот до несколь­ких тысяч электронвольт, рассеиваясь от тонкой металлической фольги или проходя сквозь нее, теряли энергию порциями. Эффект оставался непонятым до 1953 г., пока Бом и Пайнс не показали, что все это можно объяснить квантовым возбужде­нием плазмы в металле.