Электрическое поле в разных физических условиях (продолжение)

§1.Методы определения электростати­ческого поля

§2.Двумерные поля; функции комплексного переменного

§З.Колебания плазмы

§4.Коллоидные частицы в электролите

§5.Электростати­ческое поле сетки

§ 1. Методы определения электростатического поля

В этой главе мы продолжим рассмотрение характеристик электрических полей в различ­ных условиях. Сперва мы опишем один из наи­более разработанных методов расчета полей в присутствии проводников. Мы не рассчиты­ваем, конечно, что эти усовершенствованные методы будут вами тотчас усвоены. Но вам дол­жно быть интересно получить какое-то пред­ставление о характере задач, которые удается решать при помощи техники, излагаемой в спе­циальных, более глубоких курсах. Затем мы приведем два примера, в которых нет ни за­ранее фиксированных распределений зарядов, ни растекания зарядов по проводнику, а вместо этого распределение определяют другие физи­ческие законы.

Как мы выяснили в гл. 6, задача об электро­статическом поле решается очень просто, когда распределение зарядов оговорено заранее; ос­тается только взять интеграл. Когда же име­ются проводники, то возникают усложнения, потому что распределение зарядов на провод­никах с самого начала неизвестно; заряды вынуждены сами распределять себя по поверх­ности проводника так, чтобы весь проводник приобрел одинаковый потенциал. Эти задачи так просто не решаются.

Мы рассмотрели обходный путь решения таких задач, при котором сначала отыскивают эквипотенциальные поверхности некоторого заданного распределения зарядов и потом одну из них заменяют проводящей поверх­ностью. Таким манером можно составить ката­лог частных решений для проводников любой формы, плоской, сферической и т. п. Использование изображений, описанное в гл. 6, является примером косвенного способа решения. Другой такой способ мы опишем в этой главе.

Если наша задача не относится к тем, для которых годен об­ходный путь, приходится решать ее в лоб. Математической ос­новой такого способа решения задач является решение урав­нения Лапласа

(7.1)

при условии, что потенциал  на некоторой границе (поверхно­стях проводников) равен условленной константе. Задачи, свя­занные с решением дифференциального уравнения поля, удовлетворяющего некоторым граничным условиям, называются задачами о граничных значениях. Они явились предметом интен­сивного математического изучения. Для сложных проводников общих аналитических методов решения нет. Даже такая про­стая задача, как поле заряженного металлического цилиндра с запаянными торцами — консервной банки, представляет огромные математические трудности. Ее можно решить лишь приближенно, численным методом. Единственный общий метод решения — численный.

Имеется несколько задач, в которых уравнение (7.1) все же решается. К примеру, задача о заряженном проводнике, имею­щем форму эллипсоида вращения, может быть решена с по­мощью некоторых специальных функций. Решение для тонкого диска тогда можно получить, бесконечно сплющив эллипсоид. А бесконечно вытянув тот же эллипсоид, получим поле заряжен­ной иглы. Но надо подчеркнуть, что единственный прямой спо­соб, применимый всюду и всегда, это путь численных расчетов.

Задачу о граничных значениях можно также решать на ее физическом аналоге. Уравнение Лапласа возникает во многих физических ситуациях: при изучении установившегося потока тепла, безвихревого течения жидкости, отклонений упругой мембраны. Часто можно соорудить физическую модель, являю­щуюся аналогом решаемой нами электрической задачи. Изме­рив в модели величину, аналогичную интересующей нас, можно узнать решение задачи. Примером аналоговой техники являет­ся применение электролитической ванны для решения двумер­ных задач электростатики. Решение удается потому, что дифференциальное уравнение для потенциала в однородной проводя­щей среде такое же, как и в вакууме.

И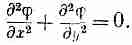 меется много физических задач, в которых физические поля в каком-то одном направлении не изменяются или этим измене­нием можно пренебречь по сравнению с изменениями в двух дру­гих направлениях. Такие задачи называют двумерными; поле за­висит только от двух координат. Скажем, если вдоль оси z про­тянуть длинную заряженную проволоку, то в точках неподалеку от нее электрическое поле зависит от x и y, а не от z; задача дву­мерная. Так как в двумерных задачах d/dz=0, то уравнение для  в свободном пространстве имеет вид

(7.2)

Поскольку двумерное уравнение сравнительно простое, то су­ществует широкий класс условий, в которых оно решается ана­литически. Действительно, существует могучая математическая техника, связанная с теоремами теории функций комплексного переменного. К изложению ее мы сейчас и перейдем.