§ 3. Замечания о векторных уравнениях

Здесь, пожалуй, уместно сделать общее замечание, касаю­щееся векторного анализа. Хотя его теоремы и доказаны в общем виде, однако, приступая к расчетам и анализу какой-либо за­дачи, следует с толком выбирать направление осей координат. Вспомните, что когда мы вычисляли потенциал диполя, то ось выбиралась не как попало, а мы направили ее по оси диполя.

Это намного облегчило нашу задачу. Потом уже уравнения были переписаны в векторной форме и сразу перестали зависеть от выбора системы координат. Теперь стало возможным выби­рать какую угодно систему координат, зная, что формула от­ныне всегда будет справедлива. Вообще нет смысла вводить произвольную систему координат, где оси направлены под ка­ким-то сложным углом, если можно в данной задаче выбрать систему получше, а уже в самом конце выразить результат в виде векторного уравнения. Так что старайтесь использовать то преимущество векторных уравнений, что они не зависят ни от какой системы координат.

С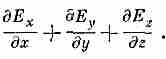 другой стороны, если вы хотите подсчитать дивергенцию какого-то вектора, то вместо того, чтобы смотреть на у•Е и вспоминать, что это такое, лучше расписать это в виде

Если вы затем вычислите по отдельности х-, у- и z-компоненты электрического поля и продифференцируете, то получите иско­мую дивергенцию. Часто при этом испытывают такое чувство, как будто произошло что-то некрасивое — словно, расписав вектор покомпонентно, потерпели неудачу; все время кажется, будто все действия надо проделывать только с векторными опе­раторами . Но часто от них нет никакого проку. Когда вы впер­вые сталкиваетесь с какой-то новой задачей, то, как правило, полезно расписать все в компонентах, чтобы удостовериться, что вы правильно представляете себе, что происходит. Нет ничего некрасивого в том, что в уравнения подставляются числа, и нет ничего неприличного в том, чтобы подставлять производные на место причудливых символов. Наоборот, в этом-то и проявляется ваша мудрость. Конечно, в специальном журнале статья будет выглядеть гораздо приятнее (да и понят­нее), если все записано в векторном виде. Но там надо эконо­мить еще и место.

§ 4. Диполъный потенциал как градиент

М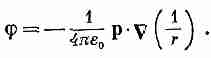 ы хотели бы теперь отметить любопытное свойство формулы диполя (6.13). Потенциал можно записать также в виде

(6.16)

Действительно, вычислив градиент 1/r, вы получите

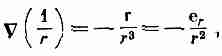
и (6.16) совпадет с (6.13).

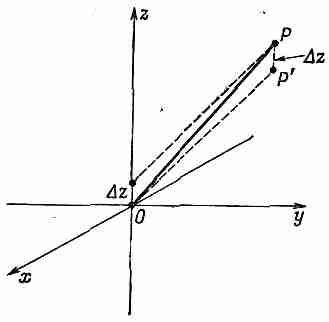
Фиг. 6.5. Потенциал в точке Р от точечного заряда, поднятого на z над началом координат, равен потенциалу в точке Р' (на z ниже Р) того же заряда, но помещенного вначале координат.

Как мы догадались об этом? Мы просто вспомнили, что e_r/r² уже появлялось в формуле для поля точечного заряда и что поле — это градиент потенциала, изменяющегося как 1/r.

Существует и физическая причина того, что дипольный по­тенциал может быть записан в форме (6.16). Пусть в начало коор­динат помещен точечный заряд q. Потенциал в точке Р(х, у, z) равен

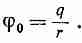
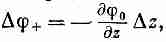( Множитель 1/4₀ опустим, а в конце мы его можем снова вста­вить.) Если заряд +q мы сдвинем на расстояние z, то потен­циал в точке Р чуть изменится, скажем на ₊. На сколько же именно? Как раз на столько, на сколько изменился бы потен­циал, если б заряд оставили в покое, а Р сместили на столько же вниз (фиг. 6.5). Иначе говоря,

где z означает то же, что и d/2. Беря ₀=q/r, мы получаем для потенциала положительного заряда

(6.17)

П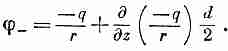 овторяя те же рассуждения с потенциалом отрицательного заряда, можно написать

(6.18)

А общий потенциал—просто сумма (6.17) и (6.18):

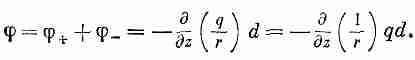
(6.19)

П ри других расположениях диполя смещение положи­тельного заряда можно изобразить вектором г₊, а уравне­ние (6.17) представить в виде

где r впоследствии надо будет заменить на d/2. Завершая доказательство так, как это было сделано выше, мы приве­дем уравнение (6.19) к виду

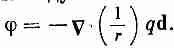
Это то же уравнение, что и (6.16). Надо только заменить qd на р и вставить потерянный по дороге множитель 1/4₀. Взглянув на это уравнение по-иному, видим, что дипольный потенциал (6.13) можно толковать как

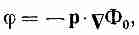
(6.20)

где Ф₀=1/4₀r — потенциал единичного точечного заряда.

Хотя потенциал данного распределения зарядов всегда мо­жет быть найден при помощи интегрирования, иногда можно сберечь время, применив какой-нибудь хитроумный прием. Например, на помощь часто приходит принцип наложения. Если нам дано распределение зарядов, которое можно соста­вить из двух распределений с уже известными потенциалами, то искомый потенциал легко получить, просто сложив уже из­вестные между собой. Наш вывод формулы (6.20) — один из примеров применения этого приема.

А вот и другой. Пусть имеется сферическая поверхность, на которой поверхностный заряд распределен пропорционально косинусу полярного угла. Интегрировать такое распределение— задача, откровенно говоря, не из приятных. Но как ни странно, на помощь приходит принцип наложения. Представьте себе шар с однородной объемной плотностью положительных зарядов и другой шар с такой же однородной объемной плотностью заря­дов, но противоположного знака. Первоначально они вложены друг в друга, образуя нейтральный, т. е. незаряженный шар. Если затем положительный шар чуть сместить по отношению к отрицательному, то нутро незаряженного шара так и останется незаряженным, но на одной стороне возникнет небольшой поло­жительный заряд, а на противоположной — такой же отрица­тельный (фиг. 6.6). И если относительное смещение двух шаров мало, то эти заряды эквивалентны существованию поверхност­ного заряда (на сферической поверхности) с плотностью, про­порциональной косинусу полярного угла.

К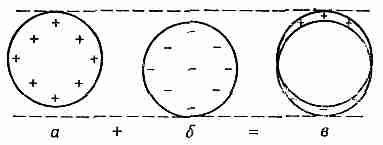 огда же нам понадобится потенциал этого распределения, то брать интегралы не нужно. Мы знаем, что потенциал каждого заряженного шара —- в точках вне его— совпадает с потенциа­лом точечного заряда. А два смещенных шара — все равно, что два точечных заряда; значит, искомый потенциал и есть как раз потенциал диполя.

Фиг. 6,6. Две равномерно заряженные сферы, вложенные друг в друга и слегка смещенные, эквивалентны неоднородному распределению

поверхностного заряда.

Таким путем можно показать, что распределение зарядов на сфере радиуса а с поверхностной плотностью

создает снаружи сферы такое же поле, как и диполь с моментом

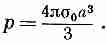
Можно также показать, что внутри сферы поле постоянно и равно

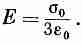
Если  — угол с положительной осью z, то электрическое поле внутри сферы направлено по отрицательной оси z. Рассмотрен­ный нами пример отнюдь не досужая выдумка составителя за­дач; он нам встретится еще в теории диэлектриков.