
Statistical physics (2005)
.pdfCase of Two Particles of Spin 1/2 |
121 |
mical properties, determined by the number of electrons that can participate in chemical bonds, are the same.
5.4Case of Two Particles of Spin 1/2
Here the properties of the wave functions of two indistinguishable particles of spin 1/2 are recalled, this is in particular the case for two electrons. From the theorem of spin-statistics connection, this wave function must be antisymmetrical with respect to the transposition of these two particles. Now, in addition to their spin degree of freedom, these two particles also have an orbital degree of freedom concerning the space coordinates; from Quantum Mechanics courses, the wave function for a single particle of this type can be decomposed into tensor products concerning the space and spin variables. The most general form of decomposition is :
ψ(r1, r2; σ1, σ2) = ψ++(r1, r2)| + + + ψ+−(r1, r2)| + − |
|
+ ψ−+(r1, r2)| − + + ψ−−(r1, r2)| − − |
(5.21) |
5.4.1Triplet and Singlet Spin States
Let us first assume, for simplification, that this decomposition is reduced to a single term, i.e.,
ψ(r1, r2; σ1, σ2) = ψ(r1, r2) |σ1, σ2 , with σ1, σ2 = ±1/2 |
(5.22) |
Since we are dealing with fermions, the two-particle wave function changes sign when particles 1 and 2 are exchanged. This sign change can occur in two di erent ways :
–either it is the space part ψ(r1, r2) of the wave function which is antisymmetrical in this exchange, the spin function remaining unchanged;
–or it is |σ1, σ2 which changes its sign in this exchange, the space function remaining unchanged.
Consider the spin states. Each particle has two possible spin states, noted | ↑ or | ↓ . There are thus four basis states for the set of two spins, which can be chosen as
| ↑↑ , | ↑↓ , | ↓↑ , | ↓↓ |
(5.23) |
(the order of notation is : particle 1, then particle 2).

122 |
Chapter 5. Indistinguishability, the Pauli Principle |
From these states one deduces four new independent states, classified according to their symmetry, that is, their behavior when exchanging the spins of the two particles.
There are three symmetrical states, unchanged when the role of particles 1 and 2 is exchanged :
|
| ↑↑ = |11 |
|
|
|||
|
|
|
|
|
|
|
|
√2 |
| ↑↓ |
| ↓↑ |
| |
|
|
|
|
|||||
|
1 |
|
|
|
(5.24) |
|
|
|
+ |
= 10 |
|||
|
|
|
|
|||
|
| ↓↓ = |1 − 1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1, with projections |
They constitute the triplet state of total |
spin S |
|||||
on the quantization axis Oz described by the respective quantum numbers Sz = +1, 0, −1 : the eigenvalue of the squared length of this spin is equal to S(S + 1) 2, i.e., 2 2 when the eigenvalue of the projection along Oz is Sz , i.e., , 0 or − .
There remains an antisymmetrical state, which changes its sign in the exchange of the two spins, this is the singlet state
1 |
| ↑↓ − | ↓↑ = |00 |
(5.25) |
√2 |
in which S = Sz = 0.
Even when the two-particle hamiltonian does not explicitly depend on spin, orbital wave functions with di erent symmetries and possibly di erent energy eigenvalues are associated with the triplet and singlet states : for example, in the special case treated in §5.2.2 the fundamental state, with a symmetrical orbital wave function [see Eq. (5.14)], must be a spin singlet state, whereas in the first excited state one can have a spin triplet. This energy splitting between the symmetrical and antisymmetrical orbital solutions is called the exchange energy or exchange interaction.
The exchange interaction is responsible of ferromagnetism, as understood by Werner Heisenberg (1901-1976) as early as 1926 : indeed the dipolar interaction between two magnetic moments a fraction of a nm apart, each of the order of the Bohr magneton, is much too weak to allow the existence of an ordered phase of magnetization at room temperature. On the contrary, owing to the Pauli principle, in ferromagnetic systems the energy splittings between states with di erent spins correspond to separations between di erent orbital levels. These are of a fraction of an electron-volt, which is equivalent to temperatures of the order of 1000 K, since these states are the ones responsible for valence bindings.

Case of Two Particles of Spin 1/2 |
123 |
In a ferromagnetic solid, magnetism can originate from mobile electrons in metals like in Fe, Ni, Co, or from ions in insulating solids, as in the magnetite iron oxide Fe3O4, and the spin can di er from 1/2. However this interaction between the spins, which relies on the Pauli principle, is responsible for the energy splitting between di erent orbital states : one state in which the total magnetic moment is di erent from zero, corresponding to the lower temperature state, and the other one in which it is zero.
5.4.2General Properties of the Wave Function of Two Spin 1/2 Particles
It has just been shown that, because of the Pauli principle, space wave functions are associated with the triplet states, which are changed into their opposite in the exchange of the two particles (antisymmetrical wave function). To the singlet state is associated a symmetrical wave function. The most general wave function for two spin 1/2 particles will be written, for a decomposition onto the triplet and singlet states :
ψ11A |11 + ψ10A |10 + ψ1A−1|1 − 1 + ψ00S |00
The wave functions of the type ψ11A are spatial functions of r1 and r2, the upper index recalls the symmetry of each component.
The same wavefunction can be expressed on the spin basis |σ1, σ2 , accounting for expressions (5.24) and (5.25) of the triplet and singlet wave functions. One thus obtains :
ψ(r, r ; σ , σ ) = ψA |
|
+ + |
|
+ |
ψ10A + ψ00S |
|
+ |
|
+ |
ψ10A − ψ00S |
|
+ |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 1 2 |
11 |
| |
|
|
|
√2 |
| |
|
− |
|
√2 |
| − |
|
|
||||
|
+ ψ1A−1| − − |
|
|
|
|
|
|
|
|
|
|
|
|
(5.26) |
||||
It thus appears, by comparing to the general expression (5.21), that the Pauli principle dictates symmetry conditions on the spin 1/2 components :
•ψ++(r1, r2) and ψ−−(r1, r2) must be antisymmetrical in the exchange of particles 1 and 2
•ψ+−(r1, r2) and ψ−+(r1, r2) do not have a specific symmetry, but their sum is antisymmetrical and their di erence symmetrical.
124 |
Chapter 5. Indistinguishability, the Pauli Principle |
5.5Special Case of N Independent Particles ; Occupation Numbers of the States
In the general case of an N -identical-particle system, the Pauli principle dictates a form for the N -particle wave function and occupation conditions for the energy levels which are very di erent in the case of fermions or bosons. In this part of the course, we are only interested by independent particles : this situation is simpler and already allows a large number of physical problems to be solved.
5.5.1Wave Function
Fermions :
We have seen that two fermions cannot be in the same quantum state and that their wave function must be antisymmetrical in the transposition of the two particles. We consider independent particles, the N -particle wave function of which takes the form of a determinant called “Slater determinant,” which indeed ensures the change of sign by transposition and the nullity if two particles are in the same state :
χ1(r1) ψ(r1, . . . , rN ) ...
χ1(rN )
χ2(...r1) |
χN (...r1) |
|
(5.27) |
||
. |
|
|
|
|
|
.. |
χ |
N |
(r ) |
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
If a state is already occupied by a fermion, another one cannot be added. A consequence is that at zero temperature all the particles cannot be in the minimum energy state : the di erent accessible levels must be filled, beginning with the lowest one, each time putting one particle per level and thus each time moving to the next higher energy level. The process stops when the N th and last particle is placed in the last occupied level : in Chemistry this process is called the “Aufbau principle” or construction principle; in solids, the last occupied state at zero temperature is called the Fermi level and is usually noted εF (see chapters 7 and 8).
Bosons :
On the other hand, the wave function for N bosons is symmetrical; in particular it is possible to have all the particles on the same level of minimum energy at zero temperature.
Special Case of N Independent Particles ; Occupation Numbers |
125 |
5.5.2Occupation Numbers
The N -fermion (or N -boson) wavefunctions are complicated to write because, as soon as a particle is put in a state of given energy, this induces conditions on the available states for the other particles; then the antisymmetrization of the total wave function has to be realized for the fermions (or the symmetrization for the bosons). Since these particles are indistinguishable, the only interesting datum in Statistical Physics is the number of particles in a defined quantum state.
Instead of writing the N -particle wavefunction, which will be of no use in what follows, we will described the system as a whole by the occupation numbers of its di erent states, this is the so-called “Fock basis” : these one-particle states correspond to distinct εk , which can have the same energy but di erent indexes if the state is degenerate (for example two states of the same energy and di erent spins will have di erent indexes k and k ); the states are ordered by increasing energies (Fig. 5.4).
εk  nk
nk
ε3  n3
n3
ε2 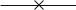 n2
n2
ε1 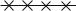 n1
n1
Fig. 5.4 : Definition of the occupation numbers of the one-particle states.
The notation |n1,2 , . . . nk , . . . will express the N -particle state in which n1 particles occupy the state of energy ε1, n2 that of energy ε2, . . . nk the state of energy εk . One must satisfy
n1 + n2 + . . . + nk + . . . = N |
(5.28) |
the total number of particles in the system. Under these conditions, the total energy of the N -particle system is given by
n1ε1 + n2ε2 + . . |
. + nkεk + . . |
. = EN |
(5.29) |
From the Pauli principle |
|
|
|
• for fermions : nk = 0 or 1 |
|
(5.30) |
|
• for bosons |
: nk = 0, 1, 2 |
. . . ∞ |
(5.31) |
126 |
Chapter 5. Indistinguishability, the Pauli Principle |
This description will be used in the remainder of the course. The whole physical information is included in the Fock notation. Indeed one cannot tell which particle is in which state, this would be meaningless since the particles are indistinguishable. The only thing that can be specified is how many particles are in each one-particle state.
5.6Return to the Introduction Examples
Now we are able to propose a preliminary interpretation of the physical phenomena described in the introduction, §5.1, some of which will be analyzed in more detail in the following chapters :
5.6.1Fermions Properties
1.In the periodic classification of the elements, the atomic levels are filled with electrons which are fermions. In a given orbital level only two electrons of distinct spin states can be placed, i.e., according to the Pauli principle they are in the singlet spin state.
2.When a chemical bond is created, the electrons coming from the two atoms of the bond go into the atomic levels originating from the coupling between the levels of the separated atoms. The resulting bonding and antibonding states must also be populated by electrons in di erent spin states, thus in the singlet spin state.
3.The ferromagnetism arises, as already mentioned, from the energy difference between the singlet and the triplet spin states for a pair of electrons. If the fundamental state presents a macroscopic magnetization, it must be made from microscopic states with a nonzero spin. In fact, in a ferromagnetic metal such as iron or nickel, the spins of two iron nuclei couple through conduction electrons which travel from nucleus to nucleus.
5.6.2Bosons Properties
4.In superconductivity the electrons of a solid couple by pairs due to their interaction with the solid vibrations. These pairs, called “Cooper pairs,” are bosons which gather into the same fundamental state at low temperature, thus producing the phenomenon of superconductivity.
5.In the same way the 4He atoms are bosons, which can occupy the same quantum state below a critical temperature (see chapter 9). Their ma-
Return to the Introduction Examples |
127 |
croscopic behavior expresses this collective property, whence the absence of viscosity.
6.Photons are also bosons and the stimulated emission, a specific property of bosons in nonconserved number, will be studied in §9.2.4.
Summary of Chapter 5
In Quantum Mechanics, the hamiltonian describing the states of identical particles is invariant under a permutation of these particles, the states before and after permutation are physically indistinguishable. This means that the hamiltonian commutes with any permutation operator : one first looks for the permutations eigenstates, which are also eigenstates of the N -particle hamiltonian.
In the case of two indistinguishable particles the symmetrical and antisymmetrical eigenstates have been described. These states have a simple expression in the case of independent particles.
Any permutation of N particles can be decomposed into a product of exchanges (or transpositions) of particles by pair : a permutation is thus either even or odd.
The Pauli principle postulates that the wavefunctions for N identical particles can only be, according to the particle’s nature, either completely symmetrical (bosons) or completely antisymmetrical (fermions) in a permutation of the particles. In particular, because their wave function is antisymmetrical, two fermions cannot occupy the same quantum state (“Pauli exclusion principle”).
The theorem of spin-statistics connection specifies that the particles of halfintegral total spin, the fermions, have an antisymmetrical wave function; the particles of integral or zero total spin, the bosons, have a completely symmetrical wave function.
In the case of two spin-1/2 particles, the triplet spin state, symmetrical, and the singlet spin state, antisymmetrical, have been described. The spin component of the wave function has to be combined with the orbital part, the global wave function being antisymmetrical to satisfy the Pauli principle.
In Statistical Physics, to account for the Pauli principle, the state of N particles will be described using the occupation numbers of the various energy
129
130 |
Summary of Chapter 5 |
levels, rather than by its wave function. A given state can be occupied at most by one fermion, whereas the number of bosons that can be located in a given state is arbitrary.
Chapter 6
General Properties of the
Quantum Statistics
In chapter 5 we learnt the consequences, in Quantum Mechanics, of the Pauli principle which applies to indistinguishable particles : they will now always be taken as independent, that is, without any mutual interaction.
We saw that it is very di cult to express the conditions stated by the Pauli principle on the N -particle wave function; on the other hand, a description through occupation numbers |n1, n2, . . . , nk , . . . of the di erent quantum states ε1, ε2, . . . εk . . . accessible to these indistinguishable particles is much more convenient. In fact we assume that the states are nondegenerate and if there are several states with the same energy, we label them with di erent indexes. Besides, it was stated that there exists two types of particles, the fermions with a half-integral spin, which cannot be more than one in any given one-particle state εk, whereas the bosons, with an integral or zero spin, can be in arbitrary number in any one single-particle quantum state.
In the present chapter we return to Statistical Physics (except in §6.4, which is on Quantum Mechanics) : after having presented the study technique applicable to systems referring to Quantum Statistics, we determine the average number of particles, at a given temperature, on an energy state of the considered system : this number will be very di erent for fermions and bosons.
This chapter presents general methods and techniques to analyze, using Statistical Physics, the properties of systems of indistinguishable particles following the Quantum Statistics of either Fermi-Dirac or Bose-Einstein, while the following chapters will study these statistics more in detail on physical examples.
131
