
Зачет по физике 2-й семестр
.doc1. Электрический заряд. Закон Кулона. Плотность заряда. Вектор плотности тока. Свойства заряда. Закон сохранения заряда. Уравнение непрерывности.
2
аспекта – заряд – свойство материи
участвовать в ЭМ взаимодействии, и заряд
- физ. величина – величина, определяющая
интенсивность ЭМ взаимодействия. Заряд:
точечный q,
пространственный Q,
элементарный e.
Если единичн. заряд помещать в ЭМ поле,
то на него сила F~q.
Берем другую частицу, на нее действует
сила
![]() .
.
![]() скорость протекания заряда. 1А – это
сила пост тока, текущего по 2м || ∞
прямолин. проводникам, ∞ малого сечения,
на расст 1м др. от др., действуют с силой
f0=2*10-7
Н/м. Атрибуты
заряда:
скаляр, действительное число, инвариантен
к преобраз. Лоренца (не зависит от
скорости), аддитивность (суммирование),
дискретность (предельная делимость).
Объемная пл-ть
скорость протекания заряда. 1А – это
сила пост тока, текущего по 2м || ∞
прямолин. проводникам, ∞ малого сечения,
на расст 1м др. от др., действуют с силой
f0=2*10-7
Н/м. Атрибуты
заряда:
скаляр, действительное число, инвариантен
к преобраз. Лоренца (не зависит от
скорости), аддитивность (суммирование),
дискретность (предельная делимость).
Объемная пл-ть![]() ,поверхностная
,поверхностная
![]() ,линейная
,линейная![]() .
Скалярное поле ρ= ρ(xyzt).
.
Скалярное поле ρ= ρ(xyzt).
![]() .
Закон
сох-я заряда
Полняй заряд замкнутой сис. сохраняется,
не изменяясь с течением t.
Пл-ть тока
.
Закон
сох-я заряда
Полняй заряд замкнутой сис. сохраняется,
не изменяясь с течением t.
Пл-ть тока
![]() .
Зная ρ и j,
можем знать все о движении заряда.
Силовые лини j.
Рисунок(силовые линии проходят круглую
площадку ) Сила тока через поток:
.
Зная ρ и j,
можем знать все о движении заряда.
Силовые лини j.
Рисунок(силовые линии проходят круглую
площадку ) Сила тока через поток:
![]() .
Рисунок (цилиндр, от его конца на некоторый
угол отходит круглая площадка, из ее
центра два вектора - прямо j
под углом к нему n.)
.
Рисунок (цилиндр, от его конца на некоторый
угол отходит круглая площадка, из ее
центра два вектора - прямо j
под углом к нему n.)
![]() .
Это совпадает с определением силы тока
данным ранее. Закон
сохранения.
Алг. сумма зарядов в замкн. сис. неизменна.
Убыль заряда в ед. t
в нек. объеме прост-ва = току через
замкнутую повер-ть ограничив. этот
объем.
.
Это совпадает с определением силы тока
данным ранее. Закон
сохранения.
Алг. сумма зарядов в замкн. сис. неизменна.
Убыль заряда в ед. t
в нек. объеме прост-ва = току через
замкнутую повер-ть ограничив. этот
объем.
![]() .Закон
сохранения заряда в дифференциальной
форме (Уравнение непрерывности.)
.Закон
сохранения заряда в дифференциальной
форме (Уравнение непрерывности.)
![]() ,т.к.
,т.к.![]() то
получим
то
получим![]() .
(переход к частной т.к. ρ ф-ция от r
и t)..
По Гаусса
.
(переход к частной т.к. ρ ф-ция от r
и t)..
По Гаусса
![]() ,то
,то
![]() (1), если инт. =0
то подинтег. Выражение=0.
Здесь он =0, т.к. V
произвольный.
(1), если инт. =0
то подинтег. Выражение=0.
Здесь он =0, т.к. V
произвольный.
![]() - закон сохр. заряда в дифф. форме (ур-е
непрерывности тока-зарядов).
- закон сохр. заряда в дифф. форме (ур-е
непрерывности тока-зарядов).
2.
Электромагнитное поле. Электрическая
напряженность, магнитная индукция.
Сила Лоренца. Закон Ампера.
ЭМ поле рассматривают как особый вид
материи. Св-ва: отсутствие четкой
локализации в пр-ве, E
и B
~ 1/rn,
где n=1,2,3…,
абсолютная проницаемость (в 1 точке
неск. не влияющих др.на др. полей). Поле
и в-во различаются только массой. У поля
есть W,
импульсом и его моментом. Эти величины
размазаны в пространстве с нек. плотностью.
Сущ. Единое ЭМ поле с двумя хар-ми Е,В(r,t)
.![]() -эл.напряженность,
-эл.напряженность,
![]() -маг.
индукция. На
заряженные тела действуют силы двух
типов: 1)Сила не зависящаа от скорости
движения -Электрическая сила
-маг.
индукция. На
заряженные тела действуют силы двух
типов: 1)Сила не зависящаа от скорости
движения -Электрическая сила
![]() .
2)Магнитная сила
.
2)Магнитная сила
![]() пропорц.
ск-ти движ. заряда и перпенд. вектору
скорости. Сила
пропорц.
ск-ти движ. заряда и перпенд. вектору
скорости. Сила
![]() называется
силой Лоренца, действует на заряд в
общем случае. Для строгого введения Е,В
рассм. Модель точечного заряда.Разобьем
тело на dV
с dQ.
На них сила dF.
Полная сила
называется
силой Лоренца, действует на заряд в
общем случае. Для строгого введения Е,В
рассм. Модель точечного заряда.Разобьем
тело на dV
с dQ.
На них сила dF.
Полная сила
![]() .
Если поле однородно, то слабая зависимость
от r,
.
Если поле однородно, то слабая зависимость
от r,
![]() ,
,
![]() .
Возьмем беск. длинный тонкий проводник.
Заменим q
на ρdV,
получим
.
Возьмем беск. длинный тонкий проводник.
Заменим q
на ρdV,
получим
![]() .
Если поле j
внутри проводника однородно:
.
Если поле j
внутри проводника однородно:
![]() .
В однородном поле закон Ампера:
.
В однородном поле закон Ампера:
![]() или
или
![]() .
Однородное поле – не зависит от коорд.
Стационарное – от времени. E
и B
исчерпывающе опис.
.
Однородное поле – не зависит от коорд.
Стационарное – от времени. E
и B
исчерпывающе опис.
3.
Уравнения Максвелла - Лоренца для
системы зарядов в вакууме.Принцип
суперпозиции.
Связь между векторами ЭМ поля с одн.
стороны и движ. порожд. это поле зарядов
с другой ст. Ур-я:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Первые два – однородные, вторые –
неоднор. В любой СИ
.
Первые два – однородные, вторые –
неоднор. В любой СИ
![]() .
Ур-я М. – дифур 1 порядка, в 1 степени –
линейные. ЭМ поле системы зарядов в
любой точке пр-ва предст. собой векторную
сумму полей каждого из зарядов в отд.
Пусть
.
Ур-я М. – дифур 1 порядка, в 1 степени –
линейные. ЭМ поле системы зарядов в
любой точке пр-ва предст. собой векторную
сумму полей каждого из зарядов в отд.
Пусть
![]() .
Линейность:
.
Линейность:
![]() .
Элемент. заряд
.
Элемент. заряд
![]() ,
элем. ток
,
элем. ток
![]() .
Они делают dE1,
dB1.
Результирующее поле будет как сумма
.
Они делают dE1,
dB1.
Результирующее поле будет как сумма
![]() ,
,
![]() .
Ур-я М. локальны в пр-ве и времени. Т.е.
связывают физические явл. в один момент
времени. В Ур-ях М. есть избыточность,
т.е. они немного связаны.
.
Ур-я М. локальны в пр-ве и времени. Т.е.
связывают физические явл. в один момент
времени. В Ур-ях М. есть избыточность,
т.е. они немного связаны.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
но т.к. есть перемен. поля, то только
,
но т.к. есть перемен. поля, то только
![]() .
.
![]() ,
,
![]() ,
закон сохр. заряда в дифференц. форме.
,
закон сохр. заряда в дифференц. форме.
4.
Система уравнений Максвелла - Лоренца
в интегральной форме. Связь уравнений
Максвелла с эмпирическими законами
электромагнетизма.
4.
![]() =>
=>
![]() По
т. Гаусса
По
т. Гаусса
![]() - инт. аналог 4 ур-я. Т. Гаусса: поток E
через замкн. пов-ть пропорц. заряду
внутри пов-ти. Окружим точечный заряд
сферой. E
и ds
совпадают по направ., поэтому скаляр
- инт. аналог 4 ур-я. Т. Гаусса: поток E
через замкн. пов-ть пропорц. заряду
внутри пов-ти. Окружим точечный заряд
сферой. E
и ds
совпадают по направ., поэтому скаляр
![]() ,
откуда
,
откуда
![]() - поле точечного заряда. Поместим заряд
q1,
- поле точечного заряда. Поместим заряд
q1,
![]() ,
получим закон Кулона как следствие
Гаусса:
,
получим закон Кулона как следствие
Гаусса:
![]() .
2.
.
2.
![]() ,
далее
,
далее
![]() .
Т.е. линии магнитного поля B
всегда замкнуты (либо в ∞). 1.
.
Т.е. линии магнитного поля B
всегда замкнуты (либо в ∞). 1.
![]() =>
=>
![]() - магнитный поток. По т. Стокса
- магнитный поток. По т. Стокса
![]() -
инт. аналог 1. Также это ЭДС индук. 3.
-
инт. аналог 1. Также это ЭДС индук. 3.
![]() =>
=>
![]() - инт. аналог 1. Где I
– сила тока
- инт. аналог 1. Где I
– сила тока
![]() ,
N
– поток вектора электрич. напряж.
,
N
– поток вектора электрич. напряж.
![]() .
Пусть пост. электрич. поле E=const.
Получим
.
Пусть пост. электрич. поле E=const.
Получим
![]() .
Т.е. закон постоянного тока. Длинный
проводник, вокруг него окружность, по
касат к ок-ти B,
в любой точке ок-ти одинаков. Циркуляция
вырождается в
.
Т.е. закон постоянного тока. Длинный
проводник, вокруг него окружность, по
касат к ок-ти B,
в любой точке ок-ти одинаков. Циркуляция
вырождается в
![]() ,
откуда
,
откуда
![]() -
Эрстед. Магн. поле может создаваться
еще и переменным эл. током (член
-
Эрстед. Магн. поле может создаваться
еще и переменным эл. током (член
![]() ).
Т.е. это закон МЭИ.
).
Т.е. это закон МЭИ.
![]() .
Из ур-я Максв. двухсторонняя связь полей.
.
Из ур-я Максв. двухсторонняя связь полей.
![]() .
.
![]() ,
,
![]() .
.
5.
Основные задачи электродинамики.
1.
Дано распределение зарядов и тока
![]() ,
,
![]() .
Найти поля
.
Найти поля
![]() ,
,
![]() .
Но поля здесь неоднозначны. Нужно доп.
условие, т.е. нач. условия при t=0.
Eнач(r)
и Bнач(r).
Также граничные условия Eгр(t,rгр),
Bгр(t,rгр).
2.
Обратная. Известны поля
.
Но поля здесь неоднозначны. Нужно доп.
условие, т.е. нач. условия при t=0.
Eнач(r)
и Bнач(r).
Также граничные условия Eгр(t,rгр),
Bгр(t,rгр).
2.
Обратная. Известны поля
![]() ,
,
![]() ,
найти
,
найти
![]() ,
,
![]() .Через
4 ур-е М. выражаем
.Через
4 ур-е М. выражаем
![]() ,
из 3 ур-я М.
,
из 3 ур-я М.
![]() .
Обычно при r->∞ E(∞)=0,
B(∞)=0.
.
Обычно при r->∞ E(∞)=0,
B(∞)=0.
6.
Общие особенности электромагнитного
поля.
Т: Любое дифференцируемое вект. поле
может быть разложено в сумму потенциал.
и вихревого полей. Поле
![]() .
Требования для потенц. поля
.
Требования для потенц. поля
![]() и
и
![]() .
Для вихр. поля
.
Для вихр. поля
![]() и
и
![]() Применяя к E,
можно
Применяя к E,
можно
![]() ,
,
![]() -
1 ур-е М. и
-
1 ур-е М. и
![]() .
К 4 ур-ю М:
.
К 4 ур-ю М:
![]() и
и
![]() .
Потенц. составл – поле источников
rot(-gradφ)=0,
вихр. сост – переменное поле. Вихревое:
чисто вихр и соленоидальное. Анализируя
III
и IV
ур-е М. divB=0,
rotB#0,
поле B
– чисто вихревое. Линии либо замкнуты,
либо на ∞. Т.е divrotA=0,
где A
– векторный магнитный потенц.
.
Потенц. составл – поле источников
rot(-gradφ)=0,
вихр. сост – переменное поле. Вихревое:
чисто вихр и соленоидальное. Анализируя
III
и IV
ур-е М. divB=0,
rotB#0,
поле B
– чисто вихревое. Линии либо замкнуты,
либо на ∞. Т.е divrotA=0,
где A
– векторный магнитный потенц.
7.
Работа, совершаемая полем при перемещении
зарядов. Есть
точечная частица m,
заряд q,
движется с V.
По 2 з-ну Ньютона
![]() .
Т.к. Vdt=r,
то
.
Т.к. Vdt=r,
то
![]() .
Посл. член=0, т.к. V||dr.
.
Посл. член=0, т.к. V||dr.
![]() .
Т.е. при действии на своб. частицу магн.
составляющая силы Лоренца работы не
соверш. Подставим
.
Т.е. при действии на своб. частицу магн.
составляющая силы Лоренца работы не
соверш. Подставим
![]() и
и
![]() ,
,
![]() .
Получим где
.
Получим где
![]()
![]() .
Где слева под пр-ной объемная плотность
мощности ЭМ поля (работа, соверш. полем
в единице объема в единицу времени).
.
Где слева под пр-ной объемная плотность
мощности ЭМ поля (работа, соверш. полем
в единице объема в единицу времени).
8.
Энергия электромагнитного поля. Плотность
и поток энергии. Вектор Пойнтинга.
Теорема об изменении энергии поля в
дифференциальной и интегральной формах.
Объемная плотность мощности
![]() .
Умножим
.
Умножим
![]() на
на
![]() и
и
![]() на
на
![]() ,
потом сложим.
,
потом сложим.
![]()
![]() .
Получили (2) :
.
Получили (2) :
![]() ,где
плотность энергии ЭМ поля
,где
плотность энергии ЭМ поля
![]() ,
а плотность потока энергии ЭМ поля
,
а плотность потока энергии ЭМ поля
![]() .
По аналогии закон сохранения заряда
.
По аналогии закон сохранения заряда
![]() .
Ур-е (2) указывает, что энергия может
переноситься через некоторую пов-ть.
Поток энергии – энергия, переносим.
потоком через некотор. пов-ть в ед.
времени. Плотность потока – поток,
приходящийся на ед. площади. S
– вектор пойнтинга. Ур-е (2) – закон
сохранения энергии в дифф. форме.
Проинтегрируем (2) по некотор. объему
.
Ур-е (2) указывает, что энергия может
переноситься через некоторую пов-ть.
Поток энергии – энергия, переносим.
потоком через некотор. пов-ть в ед.
времени. Плотность потока – поток,
приходящийся на ед. площади. S
– вектор пойнтинга. Ур-е (2) – закон
сохранения энергии в дифф. форме.
Проинтегрируем (2) по некотор. объему
![]() ,
где
,
где
![]() - энергия в объеме V.
По т. Гаусса
- энергия в объеме V.
По т. Гаусса
![]() (из 1 ур-я). Убыль энергии поля в некотор.
объеме в ед. времени равна сумме потока
энерг. через пов-ть, ограничив. данный
V
и мощности работы, соверш. полем над
зарядами в данном V.
(из 1 ур-я). Убыль энергии поля в некотор.
объеме в ед. времени равна сумме потока
энерг. через пов-ть, ограничив. данный
V
и мощности работы, соверш. полем над
зарядами в данном V.
9.
Закон сохранения энергии для замкнутой
системы "поле - заряды". Если
система замкн. – вектор Пойнтинга на
границе объема =0. (для этого в реальных
условиях E
и B
убывать быстрее чем 1/r,
и S
убывать быстрее чем 1/r2).
Тогда
![]() ,
откуда
,
откуда
![]() .
Это з-н сохранения энергии. Т.е.
.
Это з-н сохранения энергии. Т.е.
![]() ,
где втор. член =
,
где втор. член =
![]() .
Мы исходили из того, что поле действует
на частицы, ускоряя их. Но этот рез-т
справедлив также и для частиц, не имеющ.
заряда. Исчезновение в формуле потенц.
энергии связано с переходом к картине
близкодействия, тогда энергия взаимод-вия
сводится к энерг. поля.
.
Мы исходили из того, что поле действует
на частицы, ускоряя их. Но этот рез-т
справедлив также и для частиц, не имеющ.
заряда. Исчезновение в формуле потенц.
энергии связано с переходом к картине
близкодействия, тогда энергия взаимод-вия
сводится к энерг. поля.
10.
Импульс электромагнитного поля. Закон
сохранения импульса.
Получение
уравнения закона сохранения импульса
из уравнений Максвелла. Плотность
импульса. Связь между плотностями
импульса и потока энергии.
Знаем
![]() ,
где
,
где
![]() .
Подставим
.
Подставим
![]() (из 4 ур-я) и
(из 4 ур-я) и
![]() (из 3 ур-я).
(из 3 ур-я).
![]() . Добавим =0 члены
. Добавим =0 члены
![]() ,
где
,
где
![]() (из 1 з-на Максв). Получим
(из 1 з-на Максв). Получим
![]() и проинтегрируем по объему.
и проинтегрируем по объему.
![]() .
Выраж. в точках = 0, получим
.
Выраж. в точках = 0, получим
![]() ,
где
,
где
![]() .
Импульс ЭМ поля рапредел. по объему с
плотн.
.
Импульс ЭМ поля рапредел. по объему с
плотн.
![]() .
Докажем …=0. Проецируем на ось х:
.
Докажем …=0. Проецируем на ось х:
![]()
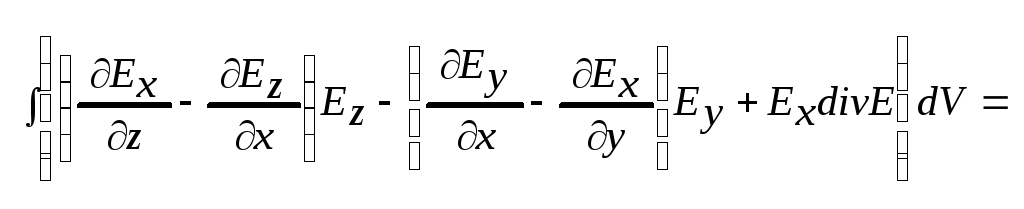
![]() (первая сумма
(первая сумма
![]() ,
вторая
,
вторая
![]() ).
Получим
).
Получим
![]() =
по т. Гаусса =
=
по т. Гаусса =
![]() (из условия замкнутости, быстрое убывание
E).
Если рассматривать движущуюся часть
энергии, то
(из условия замкнутости, быстрое убывание
E).
Если рассматривать движущуюся часть
энергии, то
![]() ,
(по аналогии с
,
(по аналогии с
![]() ).
Тогда
).
Тогда
![]() - это плотность энергии в потоке. Здесь
- это плотность энергии в потоке. Здесь
![]() ,
,
![]() .
.
![]() .
.
![]()
11.
Потенциалы электромагнитного поля.
Калибровка.
Калибровочные преобразования.
Потенц. ЭМ поля вводятся на основании
однор. ур-й Максв (I
и II).
divB=0
и divrotA=0,
А – любое вект. поле. Если B=rotA,
то II
з. Макс. будет выполняться. Любое вект.
поле A,
удовл. этому называется векторным (магн)
потенциалом.
![]() ,
=>
,
=>
![]() =>
=>
![]() ,
или
,
или
![]() .
Любое скал. поле φ(r,t),
удовл. этому, называется скалярным
(электрич) потенциалом. Потенциалы А и
φ измер. невозможно, т.о. они опред.
неоднозначно. Пусть к А добавим некоторое
потенц. поле
.
Любое скал. поле φ(r,t),
удовл. этому, называется скалярным
(электрич) потенциалом. Потенциалы А и
φ измер. невозможно, т.о. они опред.
неоднозначно. Пусть к А добавим некоторое
потенц. поле
![]() .
B'=rotA'=rotA+rotgradφ=rotA=B.
Т.е. векторный потенц. измеряется с
точностью до градиента. К φ добавим:
φ'=φ+x.
.
B'=rotA'=rotA+rotgradφ=rotA=B.
Т.е. векторный потенц. измеряется с
точностью до градиента. К φ добавим:
φ'=φ+x.
![]() .
(Первая скобка =Е).
.
(Первая скобка =Е).
![]() ,
,
![]() - это условие =0. Т.о мы знаем, как можно
преобразовывать потенциалы. Это
калибровочные преобразования, а выбор
определенных потенциалов из возможных
– калибровка.
- это условие =0. Т.о мы знаем, как можно
преобразовывать потенциалы. Это
калибровочные преобразования, а выбор
определенных потенциалов из возможных
– калибровка.
12.
Уравнения поля в потенциалах.
Калибровочные
условия Лоренца и Кулона.
Максв.:
![]() ,
,
![]() .
Подставим
.
Подставим
![]() и B=rotA.
и B=rotA.
![]() и
и
![]() .
=>
.
=>
![]() и
и
![]() .
В первом ур-и сложим члены под grad.
Поскольку A
и φ определены неоднозначно, то можно
добиться
.
В первом ур-и сложим члены под grad.
Поскольку A
и φ определены неоднозначно, то можно
добиться
![]() - это усл-е калибровки Лоренца. Получим
уравнения Даламбера:
- это усл-е калибровки Лоренца. Получим
уравнения Даламбера:
![]() и
и
![]() .
Кулоновская калибровка: пусть поле A
– чисто вихревое, divA=0.
Тогда уравнения приобретут другой вид:
.
Кулоновская калибровка: пусть поле A
– чисто вихревое, divA=0.
Тогда уравнения приобретут другой вид:
![]() и
и
![]() .
.
13.
Допустимость лоренцевой калибровки.
![]() .
Пусть не нулю, а =f(rt).
Осуществим калибровочное преобраз.
потенциалов A->A'
=A+gradψ
и φ->φ'=
.
Пусть не нулю, а =f(rt).
Осуществим калибровочное преобраз.
потенциалов A->A'
=A+gradψ
и φ->φ'=![]() и потребуем, чтобы усл-е калибровки
выполнялось для новых потенц.
и потребуем, чтобы усл-е калибровки
выполнялось для новых потенц.
![]() ,
отсюда
,
отсюда
![]() .
Т.е. снова ур-е типа Даламбера. Оно всегда
имеет решение. Если для А и φ усл-е
калибровки Лоренца не выполн., то всегда
можно совершить такое калибр. преобраз.,
чтобы для А' и φ' выполнялось.
.
Т.е. снова ур-е типа Даламбера. Оно всегда
имеет решение. Если для А и φ усл-е
калибровки Лоренца не выполн., то всегда
можно совершить такое калибр. преобраз.,
чтобы для А' и φ' выполнялось.
14.
Решение уравнений поля в потенциалах.
Общее решение ур-я Даламбера представляет
собой сумму частного решение неоднор.
ур-я и общего решения соотв. однородного
ур-я, именуемым волновым.
![]() и
и
![]() .
Осн.
задача ЭД-ки для потенц.
Нахождение полей A
и φ, удовлетв. ур-ям Даламбера с заданными
правыми частями.
.
Осн.
задача ЭД-ки для потенц.
Нахождение полей A
и φ, удовлетв. ур-ям Даламбера с заданными
правыми частями.
![]() и
и
![]() .
Дано:
.
Дано:
![]() и
и
![]() .
Найти А и φ(rt).
Для получения решения – начальные и
граничные условия.
.
Найти А и φ(rt).
Для получения решения – начальные и
граничные условия.
![]() - 4 системы н.у.
- 4 системы н.у.
![]() ,
,
![]() ,
,
![]() ,
при r
стрем. к бесконечн, =0. И
,
при r
стрем. к бесконечн, =0. И
![]() .
.
15.
Одномерное и трехмерное волновое
уравнение.
Плоские
волны.
Дано:
![]() .
Его общ. решение -
.
Его общ. решение -
![]() ,
где f1
и f2
– произвольные дифферец. ф-ции.
,
где f1
и f2
– произвольные дифферец. ф-ции.
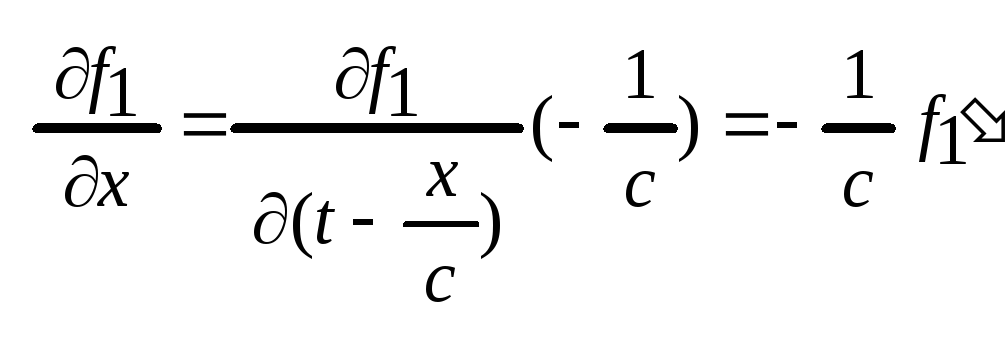 .
.
![]() .
.
![]() ,
,
![]() =>
=>
![]() ,
т.е. f1
полностью удовл. волновому ур-ю. Аналогично
и для f2.
Условие
,
т.е. f1
полностью удовл. волновому ур-ю. Аналогично
и для f2.
Условие
![]() - в различ. моменты времени ф-ция просто
передвигается вдоль оси x.
(Чертеж – оси x
и f1.
Сиськи, одна выше, др. ниже.). Т.е. значения
ее равны.
- в различ. моменты времени ф-ция просто
передвигается вдоль оси x.
(Чертеж – оси x
и f1.
Сиськи, одна выше, др. ниже.). Т.е. значения
ее равны.
![]() ,
,
![]() - ф-ция двигается со ск-тью c
в положит. напр. оси x.
Для f2,
- ф-ция двигается со ск-тью c
в положит. напр. оси x.
Для f2,
![]() - ф-ция движется со ск-тью c
в против. сторону от положит. напр. оси
x.
Волна – это процесс перемещения в пр-ве
состояния поля. Трехмерный случай:
- ф-ция движется со ск-тью c
в против. сторону от положит. напр. оси
x.
Волна – это процесс перемещения в пр-ве
состояния поля. Трехмерный случай:
![]() .
Решением является
.
Решением является
![]() ,
где
,
где
![]() ,
введем координ. ось ζ, совпадающую с
вектором k0.
=>
,
введем координ. ось ζ, совпадающую с
вектором k0.
=>
![]() .
=>
.
=>
![]() .
f1
– волна, бегущая в + напр. k0.
f2
– в против. напр. Аргументы f1
и f2
– фаза волны. Ур-е описывает плоскую
волну потенциала, т.к. пов-ть пост. фазы
в любой момент време0ни явл. пл-тью,
.
f1
– волна, бегущая в + напр. k0.
f2
– в против. напр. Аргументы f1
и f2
– фаза волны. Ур-е описывает плоскую
волну потенциала, т.к. пов-ть пост. фазы
в любой момент време0ни явл. пл-тью,
![]() .
Д-во: зафикс. момент времени
.
Д-во: зафикс. момент времени
![]() и зафиксируем момент времени t
, получим
и зафиксируем момент времени t
, получим
![]() .
Это ур-е пл-ти
.
Это ур-е пл-ти
![]() .
.
16.
Гармонические составляющие свободного
поля.
Предположим, что решение волнового ур-я
будет в таком виде:
![]() (это не проекции, а ф-ции).
(это не проекции, а ф-ции).
![]() Поделим
на φ и получим
Поделим
на φ и получим
![]() .
Каждое из слагаемых – ф-ция одной
переменной, но при произв. измен. этих
ф-ций их сумма в любой момент времени
=0, значит это не ф-ции, а определ. константы.
Соотв. после подстановки их ур-е будет
.
Каждое из слагаемых – ф-ция одной
переменной, но при произв. измен. этих
ф-ций их сумма в любой момент времени
=0, значит это не ф-ции, а определ. константы.
Соотв. после подстановки их ур-е будет
![]() .
Пример для x:
.
Пример для x:
![]() =>
=>
![]() .
Решением будет
.
Решением будет
![]() .
(Напиши для всех). ± писать бессмысленно
в силу произв. k.
.
(Напиши для всех). ± писать бессмысленно
в силу произв. k.
![]() .
Пусть
.
Пусть
![]() .
.
![]() ,
,
![]() .
.
![]() ,
пусть ω>0,
,
пусть ω>0,
![]() .
Первая волна бежит в направлении k,
вторая наоборот. Избавимся от комплексности
(просуммир. φ, беря разл. знаки).
.
Первая волна бежит в направлении k,
вторая наоборот. Избавимся от комплексности
(просуммир. φ, беря разл. знаки).
![]() .
.
![]() ,
,
![]() ,
где ω – циклич. частота.
,
где ω – циклич. частота.
![]() .
k
– волновой вектор, модуль – волновое
число, ск-ко длин волн укладывается на
2π единиц длины. Общее решение имеет
вид:
.
k
– волновой вектор, модуль – волновое
число, ск-ко длин волн укладывается на
2π единиц длины. Общее решение имеет
вид:
![]() .
Это интегр. по объему k-пространства.
.
Это интегр. по объему k-пространства.
![]() .
.
![]() - беск. малая амплитуда определ. гармоники
при определ. k.
Общее решен. волн. ур-я. – суперпозиц.
плоских гармонич. волн всевозм. амплитуд,
частот и направл. распростран. Можно
представить действ. и мним. часть потенц:
Re
Cφ(k)
и Im
Cφ(k).
Действ. решение:
- беск. малая амплитуда определ. гармоники
при определ. k.
Общее решен. волн. ур-я. – суперпозиц.
плоских гармонич. волн всевозм. амплитуд,
частот и направл. распростран. Можно
представить действ. и мним. часть потенц:
Re
Cφ(k)
и Im
Cφ(k).
Действ. решение:
![]() .
.
![]() - условие действ. потенц. Подставим
- условие действ. потенц. Подставим
![]() ,
,
![]() ,
,
![]() .
Получим
.
Получим
![]() .
Сопоставим с 1 ур-ем. Из теории интегр.
Фурье следует, что коэфф. определ.
однозначно.
.
Сопоставим с 1 ур-ем. Из теории интегр.
Фурье следует, что коэфф. определ.
однозначно.
![]() и
и
![]() .
Это необх. чтобы потенц. был действ.
Разобъем 1 ур-е на 2 инт, подст. во втор.
часть ур-я k->k'=-k
и условие, получим (соединив вновь)
.
Это необх. чтобы потенц. был действ.
Разобъем 1 ур-е на 2 инт, подст. во втор.
часть ур-я k->k'=-k
и условие, получим (соединив вновь)
![]() .
Внутри члены – комплексносопряженные.
Т.к. a+a*=2Rea.
Получим
.
Внутри члены – комплексносопряженные.
Т.к. a+a*=2Rea.
Получим
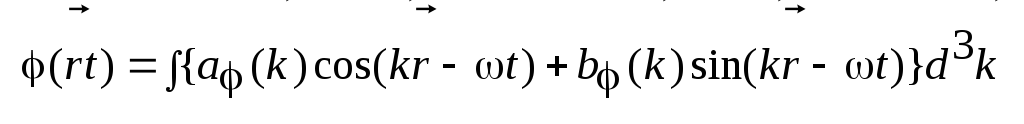 ,
где
,
где
![]() ,
,
![]() .
Для второго волн. ур-я
.
Для второго волн. ур-я
![]() .
.
![]()
