Statistical physics (2005)

From the enthalpy ∆H0, one can predict the direction of displacement of the equilibrium when the temperature increases : if ∆H0 > 0, that is, the enthalpy increases in the reaction and the reaction is endothermal, the equilibrium is thus displaced toward the right side when T increases. This is in agreement with the principle of Le Châtelier :

If a system is in stable equilibrium, any spontaneous change of its parameters must lead to processes which tend to restore the equilibrium.

As an application, the experimental data below on the dissociation of iodine allow to deduce the enthalpy of this reaction in the vicinity of 1000 K.

For a fixed total volume of 750.0 cm3, in which a total number n of molecules I2 was introduced at temperature T , the equilibrium pressure is P :

As an exercise, one can calculate Kp at each temperature and verify that ∆H0 = 157 kJ.mole−1. This reaction is endothermal.

The example presented here suggests the rich domain, but also the limitations of the applications of Thermodynamics in Chemistry : Thermodynamics does not reduce to a game between partial derivatives, as some students may believe! It allows one to predict the evolution of new reactions, from tables deduced from measures. However, only the contribution of Statistical Physics allows us to predict these evolutions from the sole spectroscopic data and microscopic models. It is this latter approach that will be followed now. Thanks to the understanding acquired in this first part of the Statistical Physics course, we will be able to deduce the constant of mass action from the quantum properties of the chemical species of the reaction.

104 Appendix 4.2

atoms, is equal to Ed = 1.542 eV, which corresponds to 17,900 K : one should bring Ed/2 per atom to move from the state I2 to the state I.

The nuclear spin of iodine has the value J = 5/2, both under the atomic and molecular forms; one assumes that no magnetic field is applied.

The splittings between energy levels of I or I2 are known from spectroscopic measures : Raman or infrared techniques give access to the distances between rotation or vibration levels; the distance between electronic levels are generally in the visible (from 1.5 eV to 3 eV) or the ultraviolet range.

One now expresses the eigenvalues of the di erent terms of HI and HI2 .

a. Translation States

One has to find the hamiltonian eigenstates : in the case of the iodine atom of mass mI,

where V (r) is the confinement potential limiting the particle presence to a rectangular box of volume Ω = LxLy Lz.

zed and for the Born-Von Kármán periodic limit conditions [ψ(x+Lx) = ψ(x)]

The translation energies εI2 tr of the molecule I2 are obtained by replacing mI by mI2 in the above expression of εItransl.

All these states are extremely close : if Ω is of the order of 1 cm3 and the dimensions of the order of 1 cm, the energy of the state nx = 1, ny = nz = 0 is given by, for I (mI = 127 g)

The distances between energy levels are in the same range, thus very small with respect to kB T , for T = 1000K.

This discussion implies that the ideal gas model is valid at room temperature for I and I2 (still more valid than for N2, since these molecules are heavier). The partition functions for their translation states will take the form (4.26)- (4.27).

b. Rotation States

The iodine molecule is linear (Fig. 4.6), its inertia momentum around an

and shows that the problem is isotropic in the center of mass frame.

Re

Fig. 4.6 : Structure of the I2 molecule.

(one recalls the definition hν = hc/λ = hcσ ; the unit cm−1 for σ is particularly adapted to infrared spectroscopy).

The selection rules ∆J = ±1 for allowed electric dipolar transitions between rotation levels correspond to εrot(J + 1) − εrot(J) = hc · 2B(J + 1).

For iodine B = 0.0373 cm−1, 2hcB/kB = 0.107 K, to be compared to HC where B = 10.6 cm−1, 2hcB/kB = 30.5 K.

The rotation levels are thus still very close at the thermal energy scale.

c. Vibration States

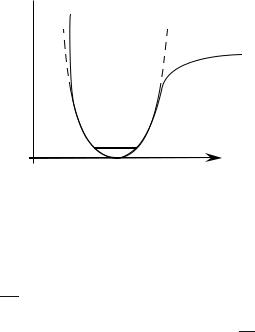
In a first approximation the vibration hamiltonian of the molecule I2 can be described as a harmonic oscillator hamiltonian, with a parabolic potential well centered at the equilibrium distance Re between the two nuclei, that is, V (R) = 12 K(R−Re)2 (Fig. 4.7). (In this figure a realistic potential is sketched in full line; the dotted line represent its approximated harmonic potential.)

ε

3

2 1

n = 0

Fig. 4.7 : Potential well associated to the vibration of the molecule I2.

with pˆR = −i ∂R∂ , µ being the reduced mass of the system. In this approximation, the vibration energies are given by

The transitions ∆ε = ω = hcσv are in the infrared domain. For I2 σv = 214.36 cm−1, which corresponds to λ = 46.7µm or hcσv /kB = 308 K (for F2 the corresponding temperature is 1280 K).

d. Electronic States

The splitting between fundamental and excited states, for both I and I2, is of the order of a few eV, corresponding to more than 10,000 K.

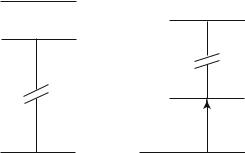
The origin of the electronic energies (Fig. 4.8) is taken at the I2 fundamental state, so that the energy of the I fundamental state is EI, with 2EI = Ed = 1.542 eV, where Ed is the dissociation energy.

εe2

εe1

εe1

g = 4

εe0

EI

g = 1

εe0

Fig. 4.8 : Electronic states of I2 and I.

e. Iodine Nuclear Spin

It is J = 5/2 on both species I and I2.

2. Description of the Statistical State of the System : Calculation of the Partition Functions

It was stated in Ch.2 that for a macroscopic system the predictions for the experimental measurements of physical parameters were the same whatever the chosen statistical ensemble. Here we will work in the canonical ensemble, where the calculations are simpler.

At temperature T , the number of iodine molecules is NI2 , the number of atoms produced by the dissociation of the molecules NI. The partition function for a single iodine molecule is written zI2 , that of an isolated atom zI. Because of the particles indistinguishability, the total canonical partition function Zc is given by :

It is related to the free energy F of the system

the partial derivatives of which, with respect to the numbers of particles, are the chemical potentials :

Since the total energy of an iodine atom or molecule is a sum of contributions, the partition function of a corresponding atom or a molecule is a product of

must be very large. Numerically λth, expressed in picometers (10−12 m), is given by

For a partial pressure equal to the atmospheric pressure and a temperature T = 1000 K, one obtains

zItr = 1.15 × 109NI zI2 tr = 3.26 × 109NI2

These numbers are huge!

b. Rotation

The factor 2J + 1 is the degeneracy of the energy level hcBJ(J + 1). Besides, the linear molecule I2 is symmetrical, so that after a 180 degree rotation one gets a new state, indistinguishable from the initial one (this would not be the case for HC for example). One thus has to divide the above expression (4.88) by two. This is equivalent to saying that the wave function symmetry allows to keep only half of the quantum states.

Since the energy distance between rotation levels is small with respect to kB T , one can replace the discrete sum by an integral

This approximation implies that zrot is a large number. Numerically, the contribution of zrot, equal to 1/2βhcB, is the ratio 1000 K/0.107 K=9346.

c. Vibration

At 1000 K, for I2, the term β ω is 0.308 : the quantum regime is valid and this expression cannot be approximated. It has the value 3.23.

d. Electronic Term

Owing to the large distances between electronic levels, one will only consider the fundamental level, four times degenerated for I, nondegenerated for I2.

At 1000 K, the term zeI is equal to 4 e−(Ed/2kB T ) = 4e−8.94 = 5.25 × 10−4, whereas for the same choice of energy origin zeI2 = 1.

3. Prediction of the Action of Mass Constant

Let us return to the definition relations (4.68) to (4.70) of Appendix 4.1,

where the µ0i are the chemical potentials under the atmospheric pressure. For our example :

The chemical potentials are expressed versus the partition functions calculated above :

Here the translation partition functions are calculated under the atmospheric pressure (standard pressure); the terms associated to the nuclear spins 2 ln(2J + 1) exactly compensate and ln ze I2 = 0.

From the data of the previous section one obtains :

Kp = e−5.6 3.7 × 10−3