12. Векторное n-мерное пространство

Пусть дана прямоугольная декартова система координат в пространстве.

Если все векторы в этом пространстве привести к общему началу в точке О (0,0,0), то координаты всех векторов совпадут с координатами их концов. Поэтому можно считать, что упорядоченные тройки вещественных чисел задают точки (или векторы) пространства. Их называют трехмерными точками (векторами).

Трехмерным векторным пространством будем называть множество всех упорядоченных троек вещественных чисел ( трехмерных векторов, трехмерных точек). Такое пространство принято обозначать R³.

По аналогии с трехмерным векторным (точечным) пространством вводится понятие n-мерного векторного пространства .

Зададим натуральное число n.

Упорядоченную совокупность n вещественных чисел будем называть n-мерным вектором (n-мерной точкой), а сами числа - его координатами (компонентами).

Множество всех n-мерных векторов будем называть n-мерным векторным (точечным) пространством и обозначим его Rⁿ.

Числовая прямая (R¹) и координатная плоскость (R²) являются частными случаями такого пространства.

Понятие равенства, сложения, вычитания, умножения на скаляр и скалярного произведения с n-мерными векторами введем аналогично соответствующим операциям с трехмерными векторами в координатной форме. Отсюда следует, что сумма двух n-мерных векторов и произведение n-мерного вектора на скаляр тоже являются n-мерными векторами.

Пространство называют линейным, если сложение элементов и умножение их на скаляр дает элемент того же пространства и при этом справедливы свойства:

Вектор О называют нулевым, а вектор -Х -противоположным вектору Х.

Векторное n-мерное пространство является линейным.

Примеры линейных пространств:

- множество всех вещественных чисел,

- множество всех многочленов не выше пятой степени с вещественными

коэффициентами,

- множество всех матриц одинаковой размерности.

По аналогии с трехмерным пространством будем считать, что скалярный квадрат вектора равен квадрату его длины.

Длину n-мерного вектора будем обозначать , тогда .

Векторное n-мерное пространство, в котором введено понятие скалярного произведения ( длины вектора ) будем называть евклидовым пространством.

Пусть даны n-мерные векторы

и вещественные числа х₁, х₂, ... ,х_j, ... х_k, которые будем называть коэффициентами.

Линейной комбинацией данных векторов назовем n-мерный вектор В,

определяемый равенством:

.

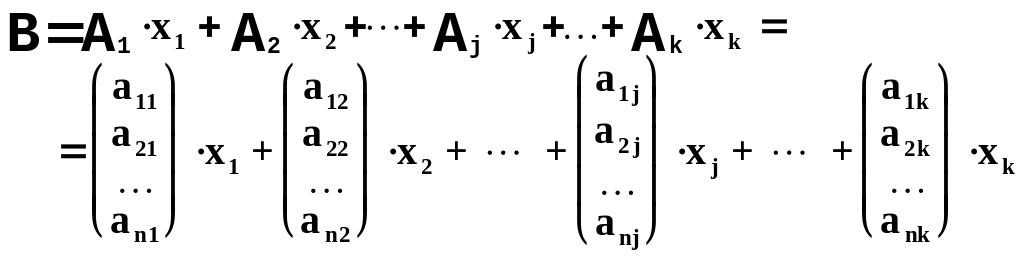Если коэффициенты являются переменными величинами, то координаты вектора В тоже будут переменными.

Векторы А₁, А₂, ... , А_к будем называть линейно независимыми, если их линейная комбинация равна нулевому вектору (В=О) только , когда все коэффициенты равны нулю. В противном случае векторы называют линейно зависимыми.

12.1. Равенство

эквивалентно системе 8.3. , у которой количество неизвестных равно k.

12.2. Максимальное количество линейно независимых n-мерных векторов

равно n.

12.3. Если среди векторов содержится нулевой вектор, то они линейно

зависимы.

12.4. Условие линейной зависимости векторов

Векторы линейно зависимы тогда и только тогда, когда хотя бы один

из них можно представить в виде линейной комбинации остальных

или когда уравнение

имеет нетривиальное (ненулевое) решение.

12.5. Векторы линейно независимы тогда и только тогда, когда уравнение

имеет только

нулевое решение.

Множество, состоящее из n линейно независимых n-мерных векторов будем

называть базисом n-мерного векторного пространства.

12.6. Любой n-мерный вектор можно единственным образом представить

в виде линейной комбинации векторов данного базиса.

Если Е₁, Е₂ , ... , Е_n - образуют базис n-мерного пространства, а

В - любой вектор этого пространства, то можно найти такой единственный набор чисел___n, при которых окажется справедливым равенство

.

Это равенство называют разложением вектора В в данном базисе, а числа ___n - координатами вектора В в данном базисе.

В матричной форме это уравнение можно записать так:

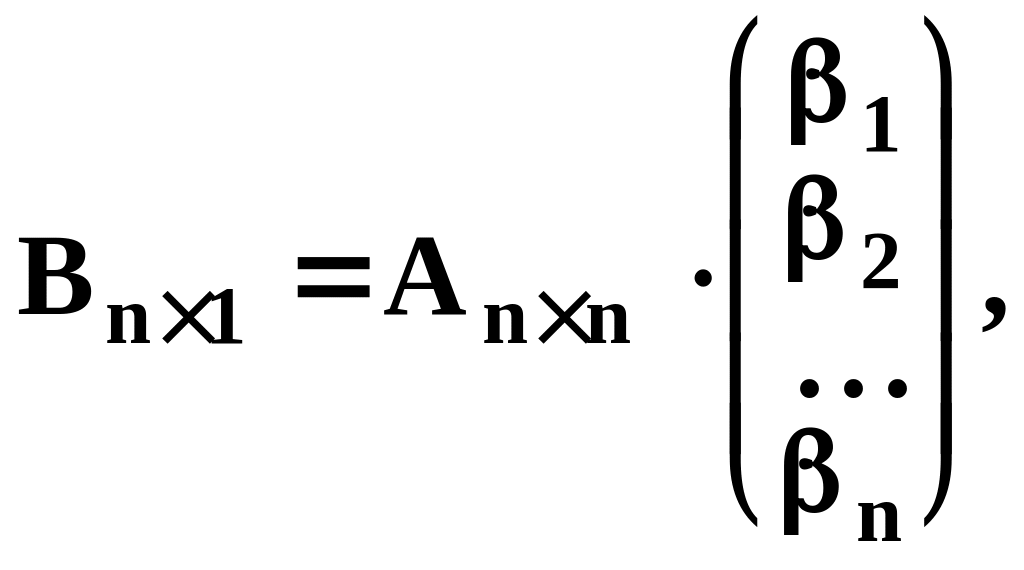
причем столбцы матрицы А являются координатами базисных векторов Е₁, Е₂, ... , Е_n.

Векторное n-мерное евклидово пространство имеет бесчисленное множество базисов и любой вектор В этого пространства имеет свои координаты в каждом.

Пример^*. Дано: векторы и  R².

Доказать: Е₁ и Е₂ образуют базис в пространстве R².

Доказательство: Базис в R²должен содержать два любых линейно независимых вектора. Векторы будут линейно независимы, если уравнение имеет только одно, причем нулевое решение.

В матричной форме уравнение имеет вид: , а в виде системы линейных уравнений его можно записать так: .

Для того, чтобы эта система имела единственное решение необходимо и достаточно, чтобы определитель этой системы был не равен нулю (теорема Крамера).

Действительно, , следовательно Е₁ и Е₂ - два линейно независимых вектора двумерного пространства и их можно рассматривать как базис этого пространства.

Пусть в n-мерном векторном пространстве задан еще один базис: D₁, D₂ , ... , D_n

и связь между старым и новым базисом задана системой векторных уравнений:

Транспонируем матрицу коэффициентов этой системы обозначим ее Р:

.

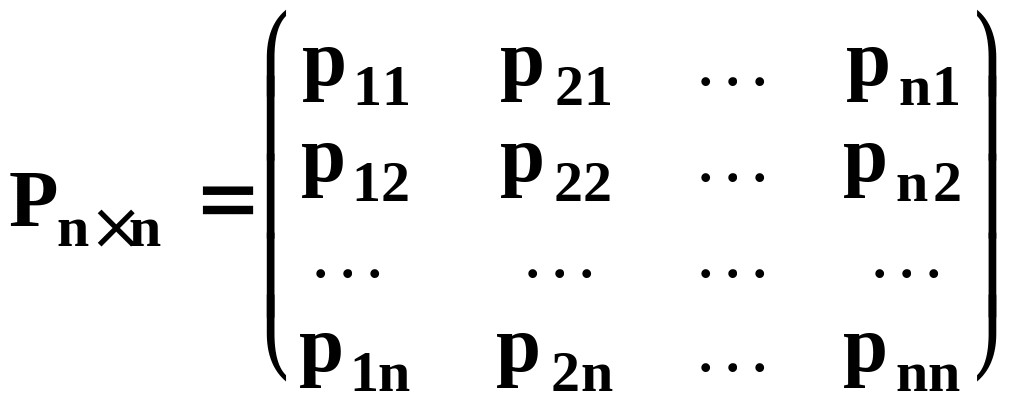Матрицу Р называют матрица перехода от старого базиса (Е₁, Е₂ , ... , Е_n) к новому базису (D₁, D₂, ... , D_n). При этом следует обратить внимание на то, что коэффициенты разложения i-го базисного вектора образуют i-й столбец матрицы Р.

Если E - матрица из старых базисных векторов, расположенных столбцами, а D - матрица из новых базисных векторов, расположенных столбцами, то связь между старым и новым базисом можно записать в виде матричных уравнений:

.

Пример **. Рассмотрим векторы D₁=-2E₁+E₂ и D₂=3E₁-2E₂ ,

где E₁ и E₂ - векторы из примера *.

Из условия следует, что .

Векторы D₁ и D₂ тоже образуют базис R² (доказательство аналогично примеру *).

Легко проверить, что .

.

Пусть дан n-мерный вектор Х, который в старом базисе задан координатами x_i, а в новом базисе координатами , i=1, 2, ..., n, при этом Р - матрица перехода от старого базиса к новому.

При таких обозначениях связь между координатами вектора Х в старом и новом базисах можно задать равенствами: .

Из всех возможных базисов чаще всего используются ортогональный базис и ортонормированный базис.

Ортогональным базисом называют базис, все векторы которого попарно ортогональны (скалярное произведение любой пары базисных векторов равно нулю).

Ортонормированным базисом называют такой ортогональный базис, все векторы которого имеют единичную длину.

Если вектор имеет одну координату =1, а остальные его координаты =0, то такой вектор называют орт. Очевидно, что количество всех ортов пространства равно его размерности. Все орты пространства образуют его ортонормированный базис.

Например, в трехмерном пространстве ортонормированный базис образуют орты

и разложение вектора с координатами 2, 3, 5 в этом базисе можно записать в виде: .

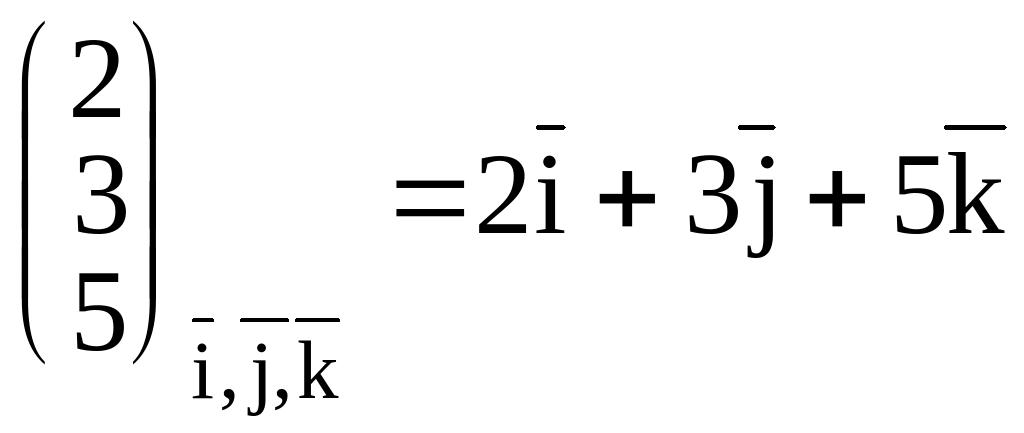На координатной плоскости (в векторном пространстве R² ) ортонормированный базис образуют два орта координатных осей.

Можно проверить, что векторы и тоже образуют ортонормированный базис этого пространства.

Если матрица Р ортогональная, то ее столбцы можно рассматривать как попарно ортогональные векторы единичной длины (см. пример 7.2.2.). Следовательно столбцы ортогональной матрицы можно рассматривать как ортонормированный базис пространства соответствующей размерности.