Министерство общего и профессионального образования

Российской Федерации

САНКТ-ПЕТЕРБУРГСКИЙ

ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ

ТЕХНОЛОГИИ И ДИЗАЙНА

КАФЕДРА МАТЕМАТИКИ

Э. Н. ОСИПОВА

ОПОРНЫЕ ЛЕКЦИИ ПО МАТЕМАТИКЕ

Часть IV

(МЕТОДИЧЕСКОЕ ПОСОБИЕ)

Санкт-Петербург

2011

СИМПЛЕКСНЫЙ МЕТОД

1. Основные понятия

Математическое программирование (МП) - это раздел математики, посвящённый решению задач о нахождении наибольшего (max) или наименьшего (min) значения функции (целевая функция) нескольких переменных, удовлетворяющих заданным ограничениям на эти переменные.

Решение задачи МП состоит из следующих этапов:

1. Моделирование задачи 1.1. выбор и обозначение переменных,

1.2. выбор и составление ограничений,

1.3. выбор построение целевой функции.

2. Решение задачи: 2.1. выбор метода (алгоритма) решения,

2.2. решение,

2.3. анализ результатов.

Модель задачи МП можно записать в виде: Требуется найти такой n–мерный вектор ,

который удовлетворяет системе ограничений вида

и максимизирует значение целевой функции .

2. Задача линейного программирования (злп) , основные понятия

Выбор метода решения зависит от вида конкретной модели. Наиболее часто используются модели задач линейного программирования (ЗЛП).

Задачами линейного программирования (ЗМП) это такой частный случай ЗМП, в которых выполняются условия: - все переменные неотрицательны,

- все ограничения имеют вид линейных уравнений или неравенств,

- целевая функция тоже линейна.

Общая модель ЗЛП имеет вид: .

В качестве примера рассмотрим задачу с двумя переменными и .

Требуется найти такой вектор , который удовлетворяет условиям:

.

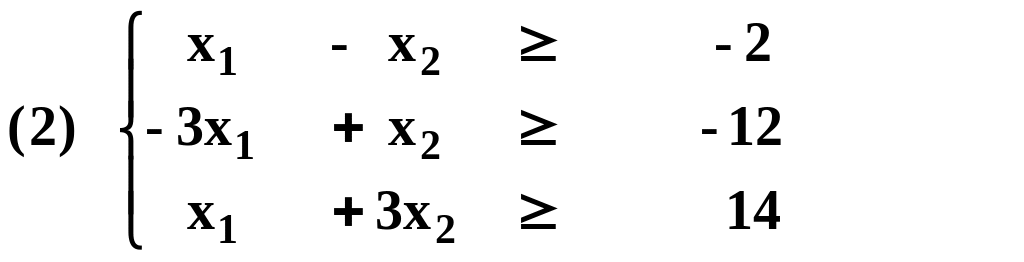
Вектор будем называть допустимым решением ЗЛП, если он удовлетворяет условиям (1) и (2). Условия (1) и (2) это пересечение полупространств и гиперплоскостей, следовательно, оно является выпуклым множеством.

Выпуклое множество, состоящее из всех допустимых решений ЗЛП, называют

область допустимых решений ЗЛП.

Для решения ЗЛП удобно пользоваться её канонической формой.

3. Приведение общей злп к канонической форме

Каноническая форма ЗЛП имеет вид:

.

Алгоритм приведения общей ЗЛП к канонической форме состоит в следющем.

1. Добиваемся, чтобы все координаты вектора В оказались неотрицательными. Если вектор В

Содержит отрицательную координату, например, , то k-ое ограничение системы умножаем на (-1). Если это ограничение было неравенством, то знак неравенства меняется на противоположный. В нашем примере система (2) примет вид:

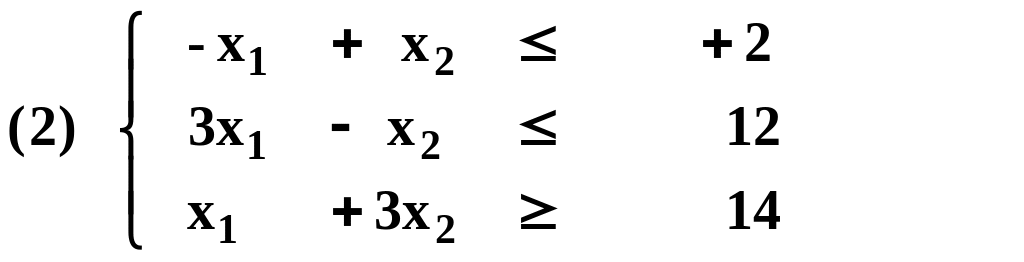
2. В каждое k-ое ограничение системы (2) вводим новую неотрицательную переменную y_k.

Если неравенство было типа , то дополнительная переменная вводится в него со знаком “-”, ( ), а если оно было типа , - то со знаком “+”, ( ). В нашем случае x₃=y₁, x₄=y₂, x₅=y₃, (Добавлено мною. Б.Т.)

В нашем примере система примет вид:

_{Таким образом, нам удалось перейти от неравенств к равенствам. Как будто бы мы к производству 2-х видов продукции добавили ещё 3 вида с тем, чтобы на складе не осталось никаких излишков товара (например, добавленная продукция 1-го вида – набор гвоздей из излишков на складе, 2- го вида – набор шурупов из излишков и т.д.)}

3. В целевую функцию z все дополнительные переменные вводятся с нулевым коэффициентом (поэтому в процессе решения и в ответе дополнительные переменные могут оказаться любыми неотрицательными числами, которые не изменяют ни условие задачи, ни целевую функцию, т.е. от наборов гвоздей и шурупов мы получаем нулевую прибыль).

В нашем примере

4. Если в условии ЗЛП требовалось максимизировать целевую функцию, то вместо неё вводим новую целевую функцию , которую следует минимизировать.

ЗЛП в канонической форме удобнее всего решать симплексным методом с использованием искусственного базиса.

Если система линейных уравнений в системе (2) канонической формы ЗЛП содержит весь ортонормированный базис, то ЗЛП можно решить симплексным методом с помощью таблиц.

Если система (2) содержит m уравнений, то ортонормированный базис состоит из векторов:

.

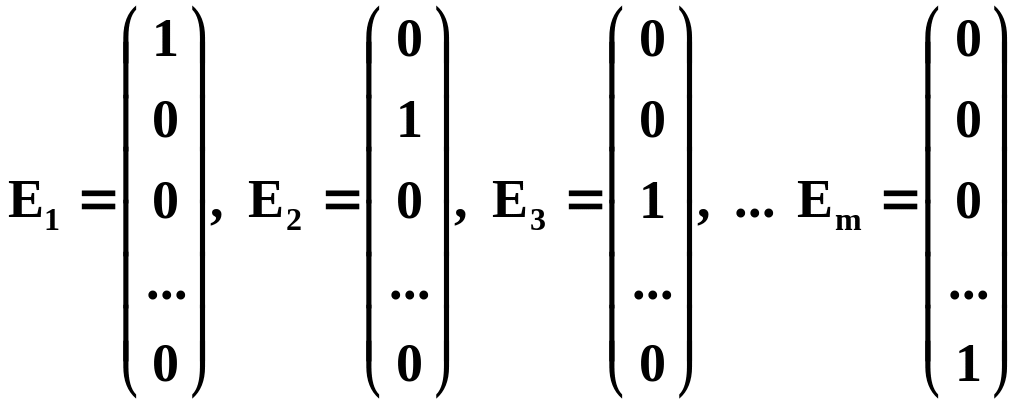Если, например, среди векторов-столбцов в системе (2) нет вектора E_k, то чтобы исправить эту «оплошность», введём в k-ое уравнение новую неотрицательную переменную w_k со знаком “+” (+w_k). В целевую функцию вводим эту переменную с коэффициентом М (+MW_k), причём будем считать, что коэффициент М – это некоторое число , которое гораздо больше, чем любые числа, которые могут встретиться при решении задачи. Эти новые неотрицательные переменные, введенные в равенства с коэффициентом “+1”, а в целевую функцию с запретительным коэффициентом “М” называют искусственными переменными, а метод решения, использующий искусственные переменные называют метод искусственного базиса.

Это как будто бы мы ввели ещё один вид продукта для рациона витаминизированного питания, но цена этого продукта (это как раз М) настолько заоблачна, что гораздо выгоднее его не использовать, т.е. взять его 0 кг.

Примечание Искусственные переменные неотрицательны и входят в целевую функцию с очень большим коэффициентом, поэтому любое решение с нулевой искусственной переменной буде гораздо лучше, чем при положительном её значении. Кроме того положительная искусственная переменная портит то равенство, в котором она находится. Поэтому искусственные переменные следует “выбрасывать” из условия задачи по мере того, как они перестают входить в базис. Забегая вперёд – нужно включать эту переменную в свободные, т.е. те, которые будут равны нулю в решении.

В нашем примере присутствует орт Е₁ (- вектор при неизвестном х₃) и орт Е₂ (- вектор при неизвестном х₄) – см. систему (2). Чтобы в системе присутствовал весь ортонормированный базис, нам нужен ещё вектор Е₃ (поскольку переменная х₅ входит с коэффициентом -1, а не +1). Следовательно, нужно в третье уравнение ввести ещё одну переменную, искусственную. Назовём её х₆ (это вместо w), в целевую функцию эта переменная войдёт с (очень большим) коэффициентом “M”. Теперь задача имеет уже 6 переменных :

.

В этом примере (для начала решения, впоследствии мы обязаны свободным сделать x₆ за счёт какоё-то другой переменной) можно свободными переменными выбрать и приравнять к нулю: , тогда базисные переменные будут .

Условия этой задачи можно занести в таблицу, которая называется симплексной и имеет вид:

	cj			-1	-3	0	0	0	М	θ	NT
i	Cб	Базис	B	А1	А2	А3	А4	А5	А6
1	0	А3	2	-1	1	1	0	0	0	2 min	0
2	0	А4	12	3	-1	0	1	0	0	0
3	М	А6	14	1	3	0	0	-1	1	14/3
		j	z0= 14М	M+1	3M+3 max	0	0	-M	0

В столбце “Базис” записываем имена векторов, образующих ортонормированный базис, а в столбце “С_б” – их “цены” из верхней строки таблицы:

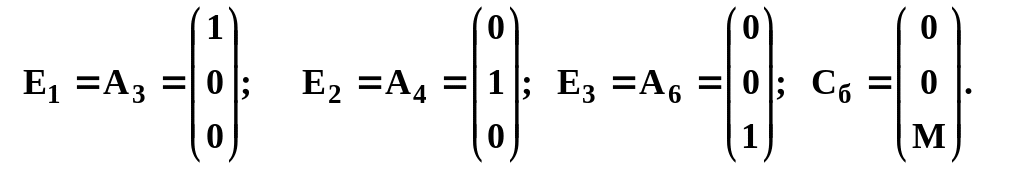
При такой записи сразу видны ненулевые значения переменных : и легко вычислить соответствующее значение целевой функции: . Впрочем, ненулевые значения мы уже получали из системы (2), см. выше. Обсудить, как получены числа, записанные в середину таблицы.

Чтобы проверить, оптимально ли найденное нами решение, нужно для каждого вектора при неизвестном вычислить оценку по формуле: .

; ;

; ;

; .

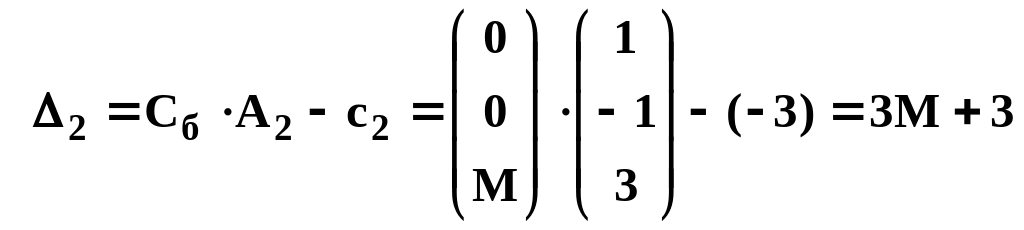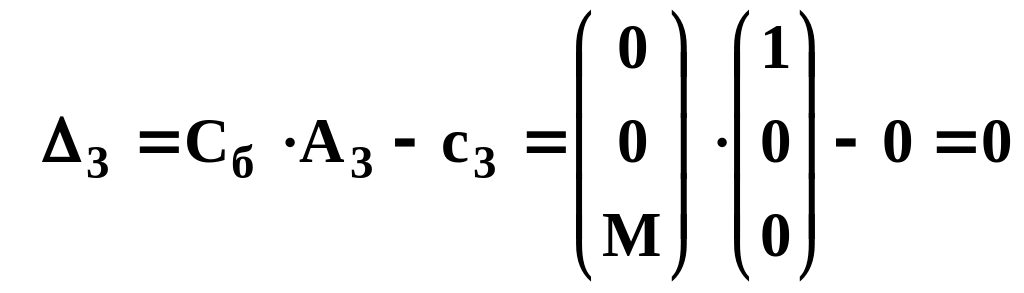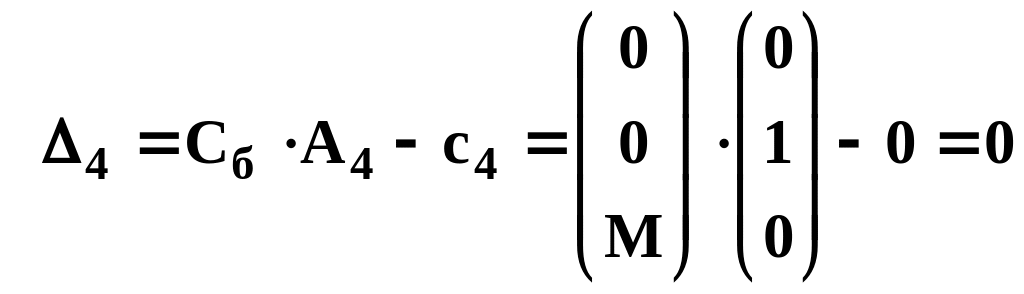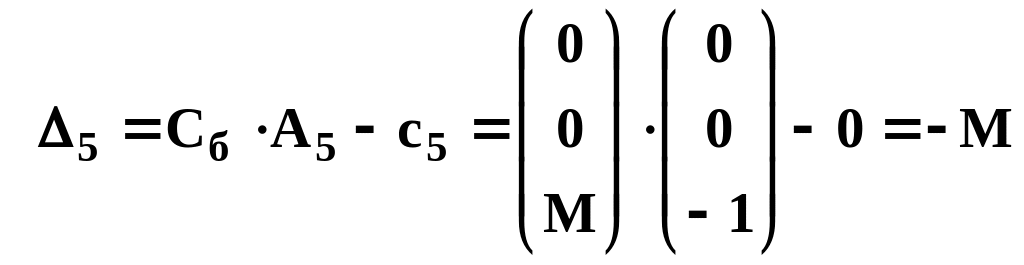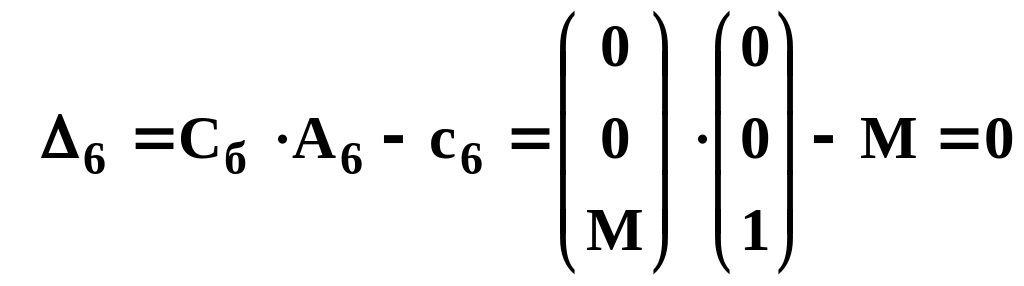С помощью вышеприведённой таблицы мы выполнили шаг решения ЗЛП симплексным методом. В результате получили х₁=0; х₂=0; z₀=14M.

Эта часть решения называется нулевым шагом или нулевой итерацией.

Проверим последнюю строку симплексной таблицы, где помещены оценки всех векторов-коэффициентов системы на оптимальность.