Министерство общего и профессионального образования
Российской Федерации
САНКТ-ПЕТЕРБУРГСКИЙ
ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ
ТЕХНОЛОГИИ И ДИЗАЙНА
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
Э. Н. ОСИПОВА
ОПОРНЫЕ ЛЕКЦИИ ПО МАТЕМАТИКЕ
1 часть
(МЕТОДИЧЕСКОЕ ПОСОБИЕ)
Санкт-Петербург
2000
ЛИТЕРАТУРА
1. Пискунов Н.С. Дифференциальное и интегральное исчислению.
-М.: Наука, 1985.-т.1-2
2. Шнейдер В.Е. и др. Краткий курс высшей математики.
-М.: ВШ, 1978.-т.1-2
3. Привалов И.И. Аналитическая геометрия.
-М.: ФМГ, 1959.
4. Берман Г.Н. Сборник задач по курсу математического анализа.
-М.: Наука, 1985.
5. Минорский В.П. Сборник задач по высшей математике.
-М.: Наука, 1987.
6. Данко П.Е. и др. Высшая математика в упражнениях и задачах в двух частях.
-М.: ВШ, 1999,-т.1-2
7. Головина Л.И. Линейная алгебра и некоторые ее приложения.
-М.: Наука, 1979
8. Гусак А.А. Высшая математика: Учебник.
-Минск.: Тетра Системс, 1998,-т.1-2
9. Кремер Н.Ш. и др. Высшая математика для экономистов.
-М.: «Банки и биржи» Изд. Объединение «Юнити», 1999
10. Краснов М.Л. и др. Вся высшая математика в двух томах.: Учебное пособие.
-М.: Эдиториал УРСС, 2000,-т.1-2
Основные обозначения
1 . Числовые множества
Понятие множества - интуитивное, не определяемое.
Множество состоит из элементов.
Множество (А) будем считать заданным, если о любом элементе известно, принадлежит он этому множеству или не принадлежит.
Множество
будем называть
пустым,
если
элемент
ему не принадлежит.
Множество может содержать конечное количество элементов (конечное множество), или бесчисленное - (бесконечное множество).
Суммой (объединением) двух множеств А и В будем называть множество С, каждый элемент которого принадлежит хотя бы одному из слагаемых:
.
Произведением (пересечением) двух множеств А и В будем называть такое множество С, каждый элемент которого принадлежит одновременно двум сомножителям:
.
Разностью двух множеств А и В будем называть такое множество С, каждый элемент которого принадлежит уменьшаемому, но не принадлежит вычитаемому:
.
.
Числовым множеством будем называть множество, все элементы которого являются числами.
1.1 Множество натуральных чисел
.
Пусть
.
При делении p на q может произойти одно из двух:
- число p
делится на число q
без остатка,
тогда запишем так:
;
- при делении числа p на число q получается частное s и в остатке r,
тогда
запишем так:
.
НОД (p, q) =d - наибольший общий делитель чисел p и q .
НОД (p, q) =d - это наибольшее из всех чисел, обладающих свойством:
.
Например, НОД(30, 42) = 6.
Если НОД (p, q) = 1, то будем говорить, что числа p и q взаимно просты.
НОК (p, q) = k - наименьшее общее кратное чисел p и q.
НОК (p, q) = k - это наименьшее из всех чисел, обладающих свойством:
.
Например, НОК(15, 6) = 30.
1.2.
Множество
целых чисел
.
.
1.3.
Множество
рациональных чисел
.
P - множество всех несократимых обыкновенных дробей.
Например,
Рациональное число можно представить и десятичной дробью, либо конечной :
, либо бесконечной
периодической :
.
1.4. Множество
иррациональных чисел
Q- это множество всех десятичных бесконечных непериодических дробей.
Например:
Множество вещественных (действительных) чисел
R - включает все перечисленные выше множества.
Любое вещественное число можно представить либо конечной , либо бесконечной десятичной дробью
.
1.6.
Абсолютная
величина числа x
-
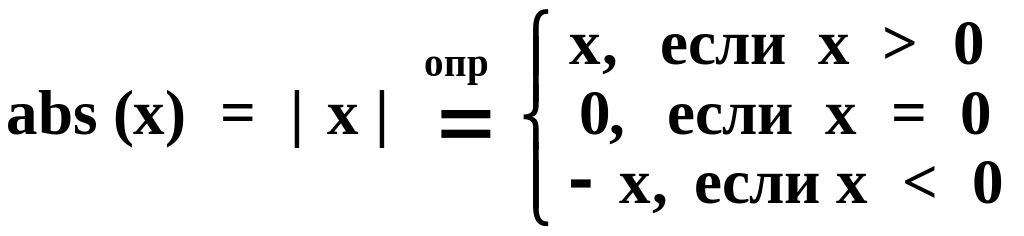
Например, | 7 | = 7; | -7 | = 7.
Свойства абсолютных величин:
1.6.1
.
1.6.2
.
1.6.3
.
1.6.4
.
1.6.5
.
1.6.6
.
.
1.7.
Знак числа х
-
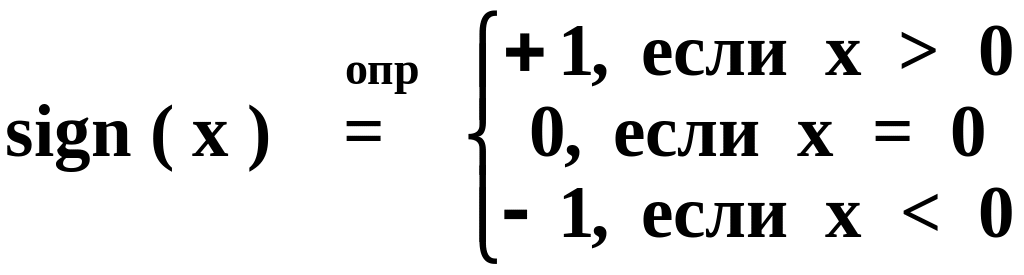
Любое вещественное число можно представить в виде:
.
Например,
1.8. Числовые промежутки
Пусть числа
причем
.
Числовым промежутком будем называть множество всех вещественных чисел х,
удовлетворяющих условиям:
- конечные промежутки:
1.8.1 закрытый (замкнутый) промежуток или отрезок
1.8.2 открытый промежуток или интервал
1.8.3 полузакрытый (полуоткрытый) промежуток
- бесконечные промежутки:
1.8.4
1.8.5
1.8.6
1.8.7
1.8.8
Множества
1.8.1 - 1.8.8
будем называть
непрерывными,
а множества
- дискретными.