
- •Свойства сходящихся рядов. Необходимое условие сходимости ряда.
- •Ряды с неотрицательными членами. Необходимый и достаточный признак сходимости ряда с неотрицательными членами.
- •Достаточные условия сходимости рядов с неотрицательными членами. Можарантный признак. Примеры.
- •Признак Даламбера сходимости рядов с неотрицательными членами.
- •Интегральный признак Коши – Маклорена сходимости рядов с неотрицательными членами. Примеры.
- •Знакочередующиеся ряды. Признак Лейбница сходимости знакочередующегося ряда.
- •Знакопеременные ряды. Абсолютная и условная сходимость знакопеременных рядов.
- •Степенные ряды. Теорема Абеля об области сходимости степенных рядов.
- •Радиус сходимости, интервал сходимости степенного ряда.
- •Свойства степенных рядов.
- •Разложение функций в степенные ряды. Теорема о единственности разложения функций в степенные ряды.
- •Ряды Тейлора и Маклорена элементарных функций.
- •Математическая статистика
- •Вариационные ряды: дискретные и интервальные. Аналитическое и геометрическое описание вр.
- •Оценивание параметров распределения случайных величин. Требования, предъявляемые к оценкам.
- •Точечные и интервальные оценки параметров распределения случайных величин
- •Метод максимального правдоподобия (Фишере) точечного оценивания параметров распределения случайных величин. Примеры.
- •Метод моментов (Пирсона) точечного оценивания параметров распределения случайных величин. Примеры.
- •Критерии Фишера и Стьюдента проверки статистических гипотез. Примеры
- •3. Математические методы м математические модели в экономике
- •Функции предложения и функции спроса, равновесная цена и равновесный объём. Примеры.
- •Макроэкономическая балансовая модель Леонтьева «затраты – выпуск».
- •Оптимизационные задачи с ограничениями. Модель максимизации прибыли предприятия.
- •Общая постановка задачи линейного программирования (злп). Графическое решение двумерных злп. Примеры.
- •Многомерные задачи злп. Понятие о симплекс- методе.
- •Специальные злп. Транспортная задача.
- •Основные понятия и определения математической теории игр. Антагонистическая игра (игра с нулевой суммой).
- •Минимаксная стратегия игры. Верхняя и нижняя цена игры. Определение оптимальных стратегий.
- •Теорема фон-Неймана о существовании оптимального решения конечной матричной игры.
- •Теорема фон-Неймана об активных стратегиях. Методы упрощения платежной матрицы.
- •Решение игр в чистых стратегиях и седловые точки матрицы игры.
- •Аналитическое решение игры (2 × 2), графическое решение игр вида (2 X n) и (n X 2).
- •Приведение матричной игры к злп.
- •Игры с природой. Постановка задачи. Математическая модель.
Радиус сходимости, интервал сходимости степенного ряда.
Интервал
![]() называется
интервалом
сходимости степенного ряда.
радиус
сходимости степенного ряда – есть
интервал, отрезок (-R,R),
внутри которого степенной ряд имеет
конечную сумму, которая определяется
фун-ей f(x)
называется
интервалом
сходимости степенного ряда.
радиус
сходимости степенного ряда – есть
интервал, отрезок (-R,R),
внутри которого степенной ряд имеет
конечную сумму, которая определяется
фун-ей f(x)
Радиус
сходимости степенного ряда.
Если
существует предел
![]() ,
то радиус сходимости ряда
,
то радиус сходимости ряда
![]() равен
равен
![]() .
Доказательство.
Рассмотрим ряд
.
Доказательство.
Рассмотрим ряд
![]() .
По
условию существует
.
Обозначим
его через
.
По
условию существует
.
Обозначим
его через
![]() .
Тогда
.
Тогда
![]() .
При каждом значении
степенной ряд становится
числовым. Поэтому по признаку
Даламбера ряд
сходится,
если
.
При каждом значении
степенной ряд становится
числовым. Поэтому по признаку
Даламбера ряд
сходится,
если
![]() ,
т.е.
,
т.е.
![]() .
по
теореме 14.10 о сходимости знакопеременных
рядов ряд
также сходится при
,
причем абсолютно. При
.
по
теореме 14.10 о сходимости знакопеременных
рядов ряд
также сходится при
,
причем абсолютно. При
![]() ряд
расходится, так как
ряд
расходится, так как
![]() и, следовательно,
общий член ряда
и, следовательно,
общий член ряда
![]() не стремится к нулю при
.
данный ряд сходится внутри интервала
и
расходится вне его, т.е. радиус
сходимости равен
.
не стремится к нулю при
.
данный ряд сходится внутри интервала
и
расходится вне его, т.е. радиус
сходимости равен
.
Свойства степенных рядов.
Пусть
функция
является
суммой степенного ряда
![]() ,(6)
,(6)
интервал сходимости которого (— R, R). В этом случае говорят, что на интервале (— R, R) функция f(х) разлагается в степенной ряд (или ряд по степеням х). Имеют место две теоремы о свойствах степенных рядов.
Теорема
4.
Если
функция f
(х) на интервале (—R,
R)
разлагается в степенной ряд (6),
то она
дифференцируема на этом интервале и ее
производная
![]() может быть найдена почленным
дифференцированием ряда (6),
т.
е.
может быть найдена почленным
дифференцированием ряда (6),
т.
е.
![]()
![]() Аналогично
могут быть вычислены производные любого
порядка функции f(х).
При этом соответствующие ряды имеют
тот же интервал сходимости, что и ряд
(6).
Аналогично
могут быть вычислены производные любого
порядка функции f(х).
При этом соответствующие ряды имеют
тот же интервал сходимости, что и ряд
(6).
Теорема
5.
Если
функция f
(х) на интервале (-
R,
R)
разлагается в степенной ряд (6),
то
она интегрируема в интервале ( —
R,
R)
и интеграл от нее может быть вычислен
почленным интегрированием ряда (6),
т.
е. если
![]() ,
то
,
то![]()
![]() Представляет
интерес интегрирование степенного ряда
(6) по отрезку [0, х],
где
:
Представляет
интерес интегрирование степенного ряда
(6) по отрезку [0, х],
где
:
![]() В
этом случае опять получаем степенной
ряд, который имеет тот же интервал
сходимости, что и ряд (6).Сформулированные
теоремы дифференцирования и интегрирования
степенных рядов имеют важное значение.
Далее они неоднократно используются.
В
этом случае опять получаем степенной
ряд, который имеет тот же интервал
сходимости, что и ряд (6).Сформулированные
теоремы дифференцирования и интегрирования
степенных рядов имеют важное значение.
Далее они неоднократно используются.
Разложение функций в степенные ряды. Теорема о единственности разложения функций в степенные ряды.
Если функция f(х) на интервале (-R, R) разлагается в степенной ряд ,(8)
то это разложение единственно.
Доказательство. По условию ряд (8) сходится на интервале (-R, R) и функция f(х) — его сумма. Следовательно, на основании теоремы 14.14 ряд (8) можно почленно дифференцировать на интервале ( -R, R) любое число раз. Дифференцируя, получаем
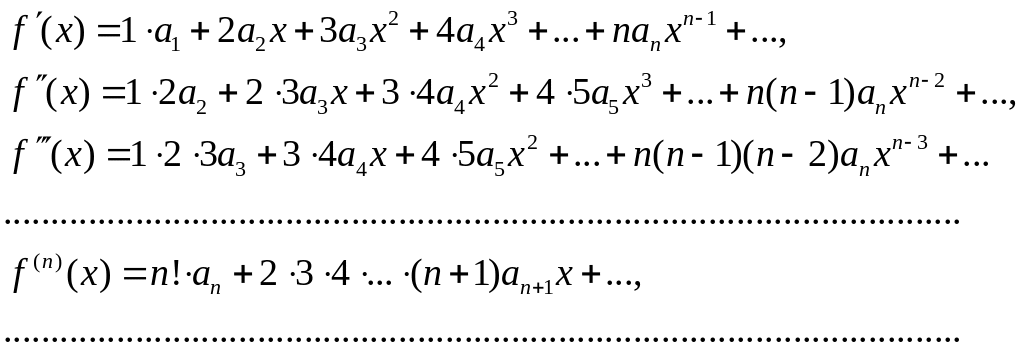 Полагая
в полученных равенствах и в равенстве
(8)
,
имеем
Полагая
в полученных равенствах и в равенстве
(8)
,
имеем
![]() откуда
находим
откуда
находим
![]() (9)
(9)
Таким образом, все коэффициенты ряда (8) определяются единственным образом формулами (9), что и доказывает теорему.
Ряды Тейлора и Маклорена элементарных функций.
если
функция
разлагается
в степенной ряд, то этот ряд имеет вид![]() (10)
Ряд
(10) называется рядом
Маклорена для
функции f(х).
(10)
Ряд
(10) называется рядом
Маклорена для
функции f(х).
Для
того чтобы ряд Макларена (10)
сходился
на (—
R,
R)
и имел своей суммой функцию f(x),
необходимо и достаточно, чтобы на (—R,
R)
остаточный член Rn(x)
формулы Маклорена (11)
стремился
к нулю при
,
т.
е.
![]() для любого
для любого
![]() .
.
Доказательство.
Необходимость.
Пусть
функция f(x)
—
сумма ряда Маклорена на (-R,
R),
т.
е.
![]() .
Тогда
из равенства (12) следует, что
для любого
.
Достаточность.
Пусть
для
любого
.
Тогда
из равенства (12) следует, что
.
Тогда
из равенства (12) следует, что
для любого
.
Достаточность.
Пусть
для
любого
.
Тогда
из равенства (12) следует, что
![]() ,
т. е.
.
Это и означает, что ряд Маклорена (10)
сходится на (-R,
R)
и
его сумма равна f(х).
Теорема
доказана
,
т. е.
.
Это и означает, что ряд Маклорена (10)
сходится на (-R,
R)
и
его сумма равна f(х).
Теорема
доказана
