2. Дробово-лінійна функція

Означення2. Функція (c≠0) називається дробово-лінійною.

Для дробово-лінійна функція має похідну та якщо (випадок, коли нецікавий, бо тоді ), то при та відображення здійснює конформне відображення усіх z ( ).

Оскільки 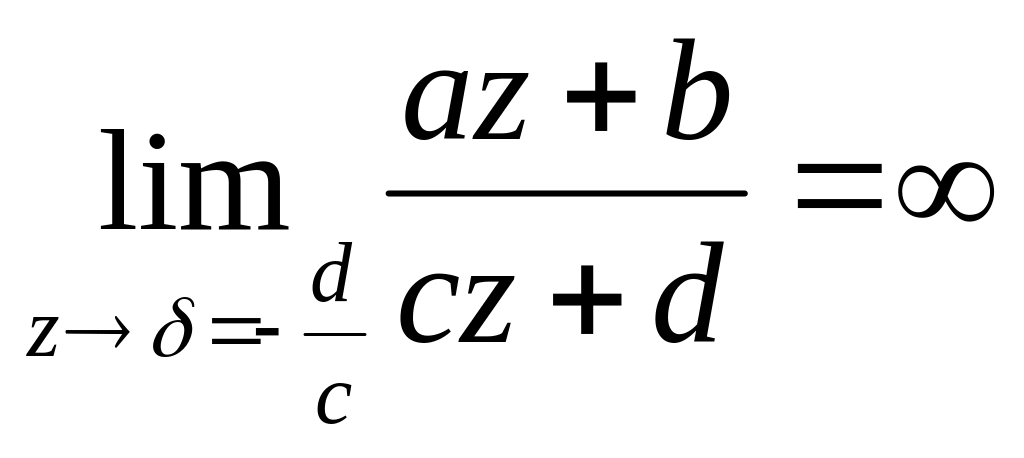, , то довизначивши , отримаємо, що переводе розширену комплексну площину z на розширену площину .

З знаходимо, що – обернена функція до , причому , тобто обернена функція до – дробово-лінійна та є однолистим відображенням розширеної площини z на розширену площину . Враховуючи все, що було сказано вище, можна зробити висновок, що – конформне відображення розширеної площини z ( ) на розширену площину .

Залишається розглянути – чи конформне відображення у точках ?

Із визначення конформності відображення у нескінченно віддаленій точці, треба розглянути конформність відображення у точці z=0, та існує, тобто – конформне відображення у z=0, значить у точці здійснює конформне відображення.

Нехай . Розглянемо функцію , обернену до вихідної . Оскільки дробово-лінійна функція – конформне відображення, то відображення зберігає кути та постійність розтягувань при відображенні у , але тоді і в обернену сторону відображення (обернена до ) зберігає кути та постійність розтягувань при відображенні у .

Таким чином, можна зробити висновок: дробово-лінійна функція здійснює конформне відображення розширеної комплексної площини z на розширену комплексну площину .

Теорема1. Заданням відповідності трьом різним точкам розширеної площини z трьох різних точок розширеної площини дробово-лінійна функція визначена однозначно.

Тобто, якщо , , , то має вид

: = : .

Теорема2 (колова властивість). Дробово-лінійна функція переводе кола та прямі на площині z у кола та прямі на площині .

Доведення теореми див. [1, с. 162-163].

Приклад1. Знайти функцію, яка конформно відображає коло на верхню півплощину .

Розв’язання.

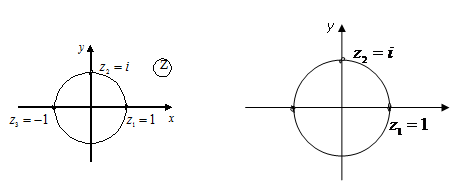
Встановимо відповідність:

(границя повинна переходити в границю) та повинно зберігатися направлення обходу області тоді, оскільки дробово-лінійна функція буде мати вид = : або .

Знайдемо . Відмітимо, що , тобто переводе коло на півплощину .

Вправи

У що відображаються наступні області?

1. квадрат ;

2.півколо .

Знайти дробово-лінійне відображення, яке переводе точки –1,i,i+1 у точки

3. 0, 2i, 1– i ;

4. i, ,1.

Знайти дробово-лінійне відображення, яке переводе точки -1, у точки

5. i, 1, 1+i;

6.

Знайти загальний вид дробово-лінійного відображення, яке переводе:

7. верхню півплощину на себе;

8. верхню півплощину на нижню;

9. верхню півплощину на одиничне коло;

10. верхню півплощину на праву півплощину.

3. Степенева функція. Поверхня Рімана

Означення3. Функція називається степеневою.

Визначена та однозначна на всій розширеній площині z, z= ставимо у відповідність .

Оскільки та для будь-якого , то у всіх зберігає кути та постійність розтягувань. При кути не зберігаються. Дійсно, якщо такі, що , , то , тобто кут між та дорівнює та збільшується у n разів згідно з кутом між .

Аналогічно з z= .

Теорема3. Сектори взаємно однозначно, а значить і конформно відображаються на площину з вирізаним променем .

Доведення [1,2,3].

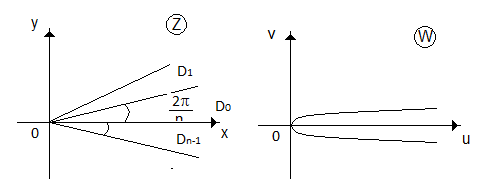
Причому границя області відображається у верхній берег розрізу , а границя у нижній берег розрізу, .

Розіб’ємо всю площину z на сектори , тоді сектору взаємно-однозначно ставить у відповідність площину з розрізом по променю . Позначимо - вказану площину відповідну , таких площин буде . Для взаємно-однозначного образу всієї розширеної площини z візьмемо n „листків” площини та розмістимо ці „листки” один над одним так, щоб точки з однаковими координатами були розміщені один над другим. „Склеїмо” розміщені один над одним „листки” по тим берегам розрізу , які є образами одного і того ж променя , який є загальною границею двох сусідніх секторів. Тобто, нижній берег розрізу з’єднаємо з верхнім берегом розрізу , вільний нижній берег розрізу – з верхнім берегом розрізу і так далі та, нарешті, нижній берег розрізу листка та верхній берег розрізу (останнє з’єднання потрібно розуміти у змісті ототожнення точок з однаковими абсцисами відповідних берегів розрізів та ). Крім того, у всіх площин „склеїмо” точки z=0 та z= . Отриману n–„листкову” замкнену поверхню називають поверхнею Римана значень функції .

Із всього вище сказаного можна зробити висновок: функція здійснює взаємно-однозначне відображення розширеної площини z на поверхню Римана, яке є конформним у всіх точках площини z, крім z=0 та z= .

Приклад1. Відобразити кут на верхню півплощину.

Розв’язання. відображає вказаний кут на нижню півплощину за властивостями степеневої функції. Тепер нижню півплощину потрібно відобразити у верхню. Це можна зробити за допомогою повороту на або радіан, тобто шукана функція має вид .

Вправи

1) відобразити кут на верхню півплощину;

2) кут на праву півплощину;

3) кут на нижню півплощину;

4) кут на ліву півплощину;

5) кут на коло ;

6) кут на коло .

Знайти образ областей при відображенні:

7) , ;

8) , ;

9) , ;

10) ,