Контрольна робота (заочна форма навчання)

Варіант 1

1. Обчислити всі значення та виділити головне значення.

2. Перевірити умови Даламбера—Ейлера для функції і знайти .

3. Виходячи з означення комплексного інтеграла, обчислити 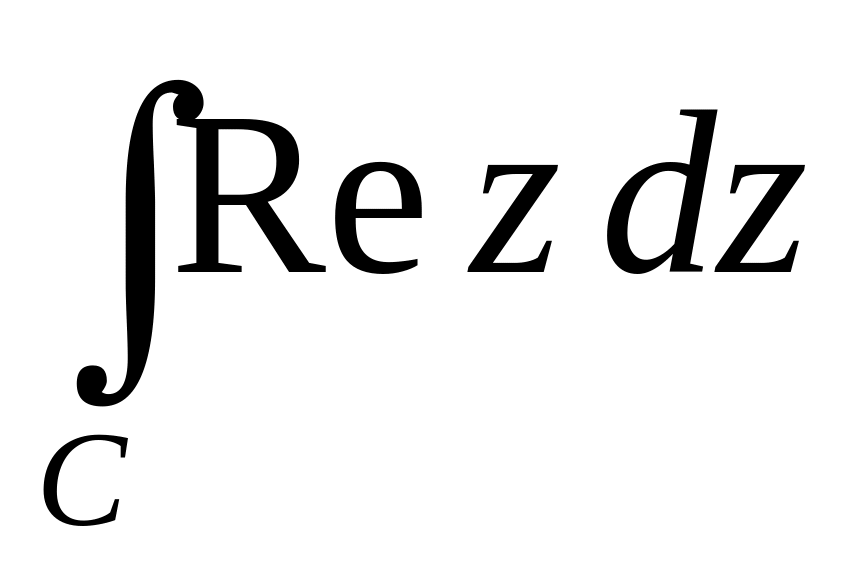, де С – півколо (початок в точці ).

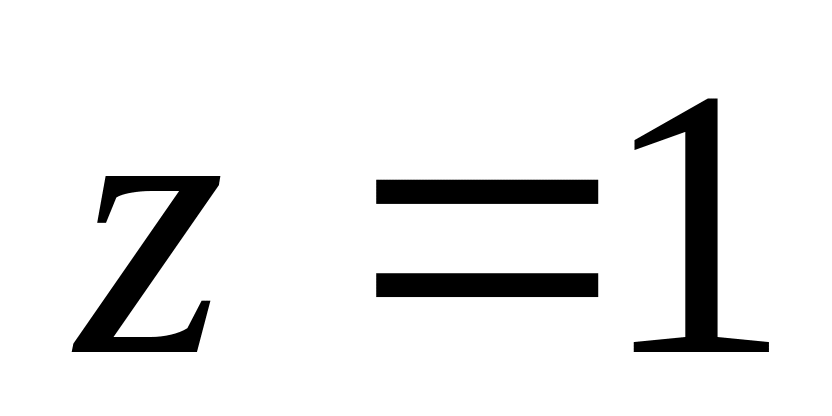4. Знайти радіус збіжності степеневого ряду

5. Знайти лишки функції 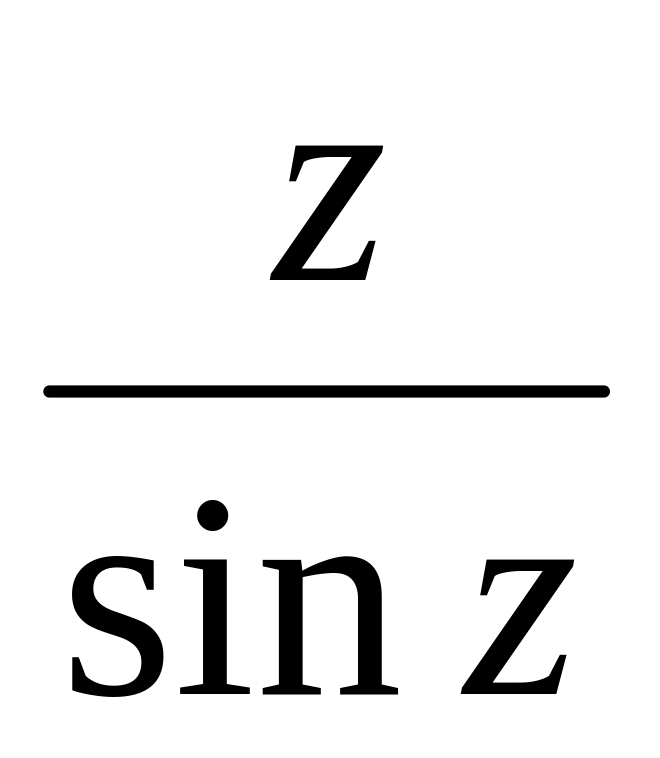відносно всіх її полюсів.

6. На яку область в площині функція відображає круг ? Як відображаються при цьому, зокрема, кола , (0 < < 1) і радіуси ?

Варіант 2

1. Знайти всі ті значення , при яких 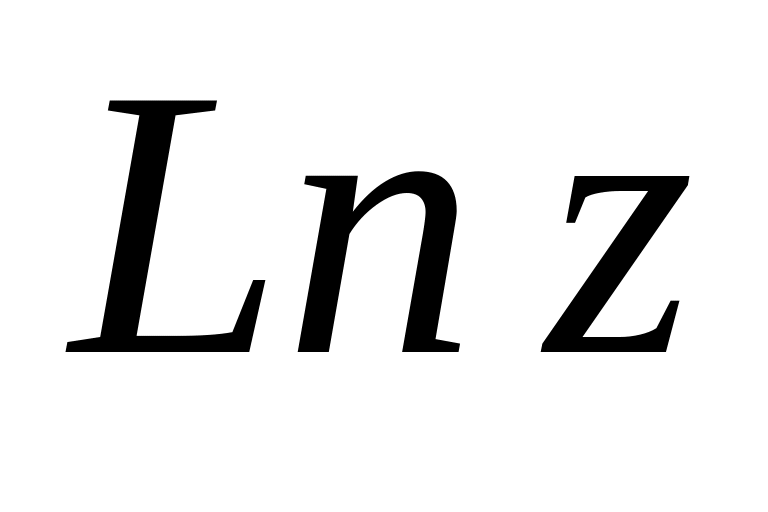є чисто уявним числом.

2. Те ж саме для функції .

3. Те ж саме для 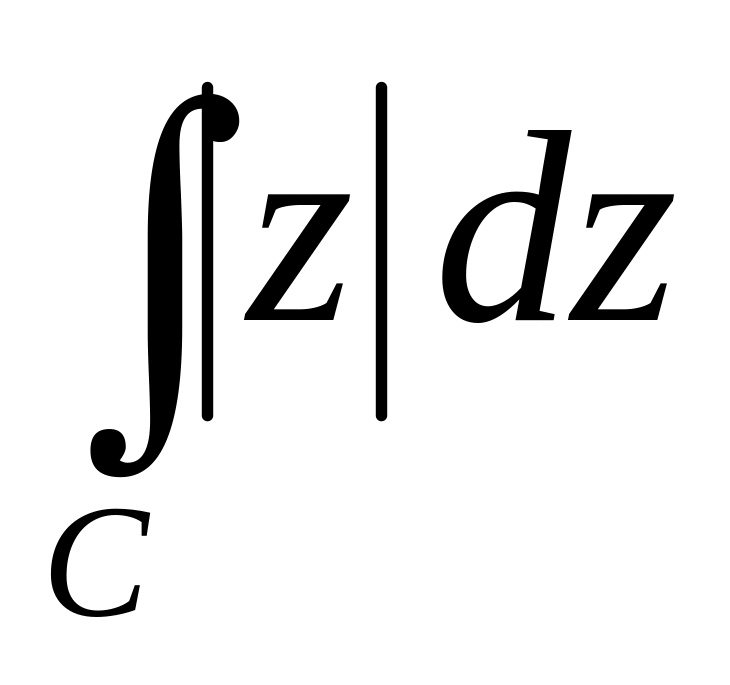, де С — радіус-вектор точки .

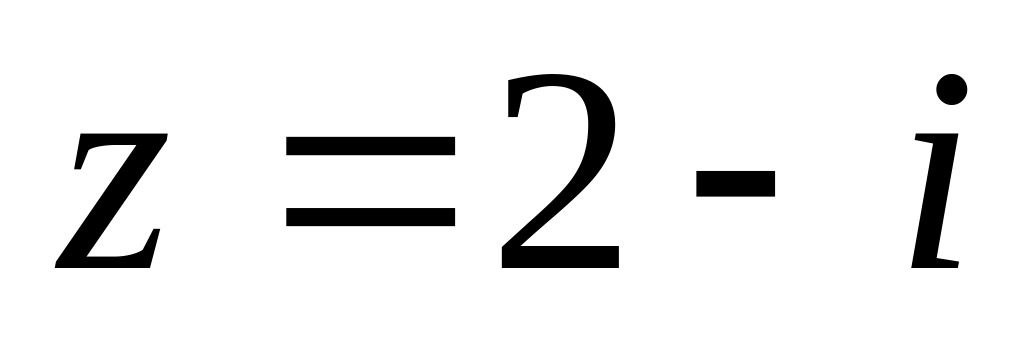4. Знайти радіус збіжності степеневого ряду

5. Знайти лишки функції відносно всіх її полюсів.

6. Для функції , де 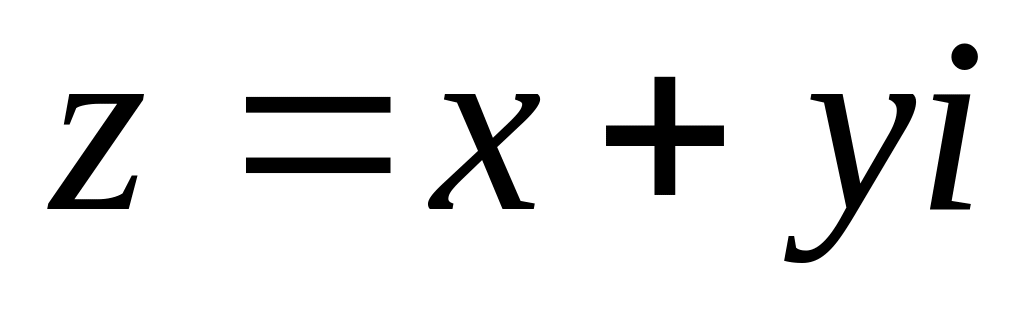, знайти образи ліній .

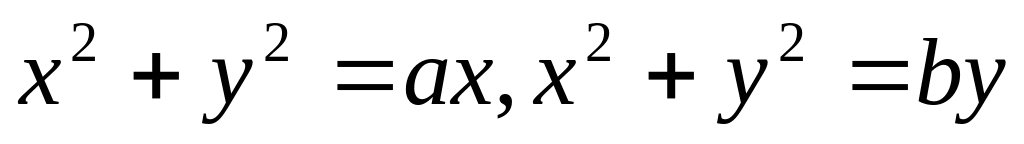Варіант 3

1. Знайти модуль і головне значення аргументу числа .

2. Знайти аналітичну функцію аргументу , дійсна частина якої .

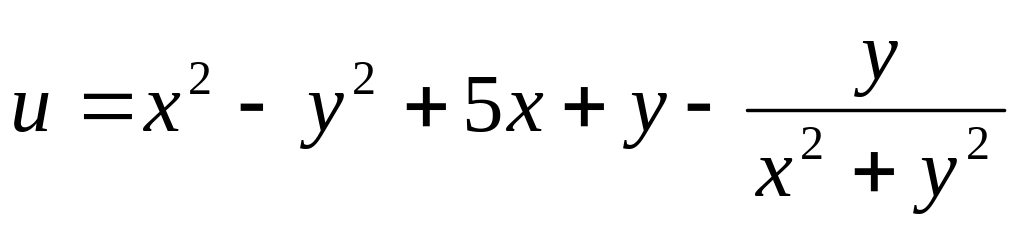3. Користуючись інтегральною формулою Коші, обчислити інтеграл 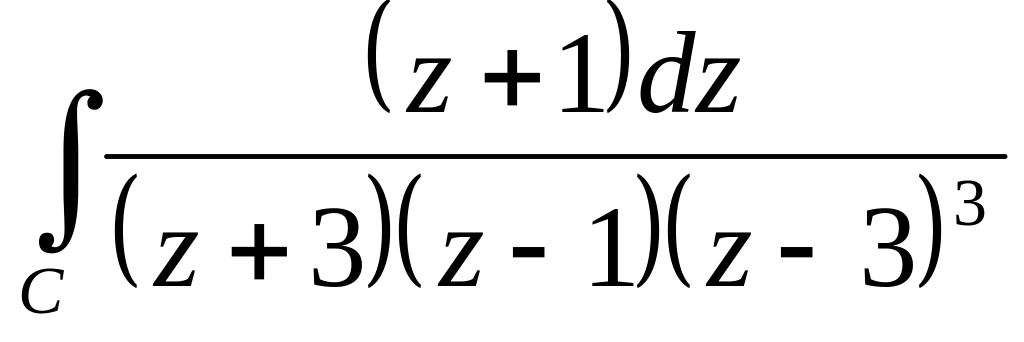, де С— коло .

4. Знайти область збіжності функціонального ряду

5. Чому рівний інтеграл , взятий по колу 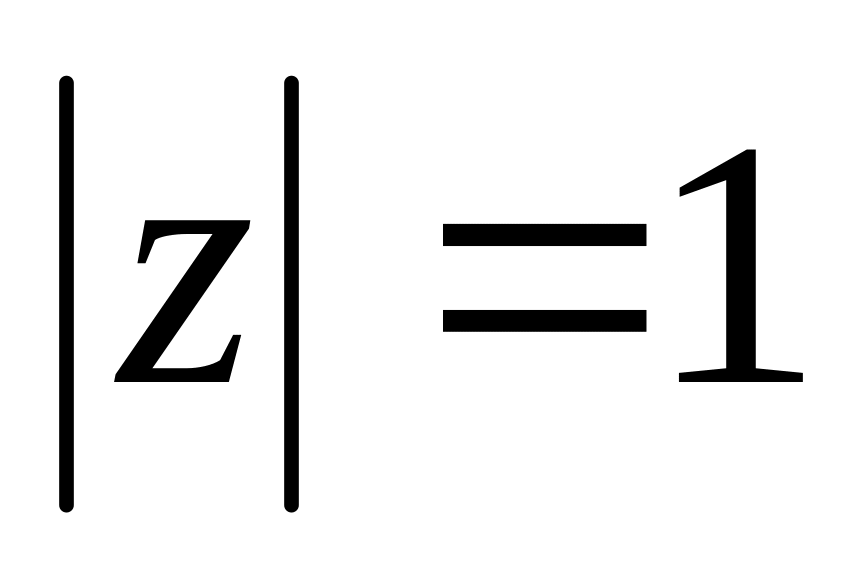? Порівняти його з інтегралом

6. Знайти лінію в площині 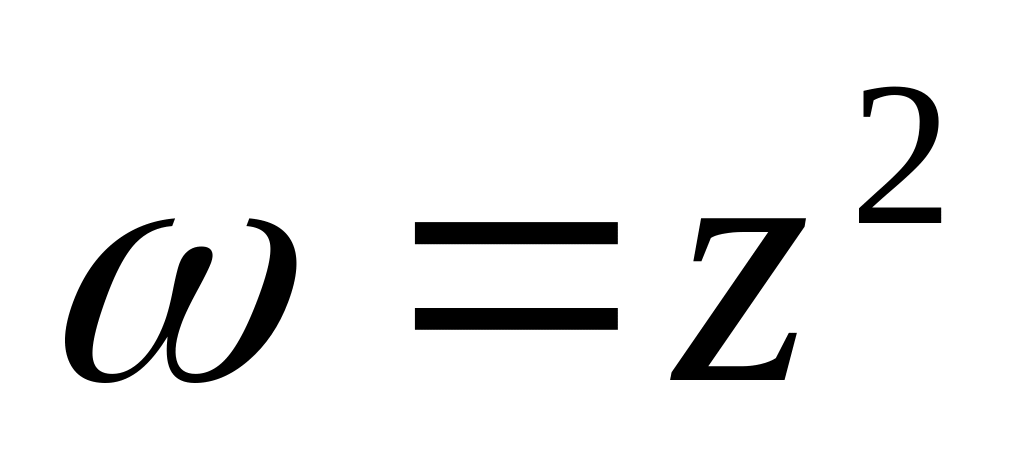, яку описує точка, якщо точка z н z- площині рухається по відрізку прямої .

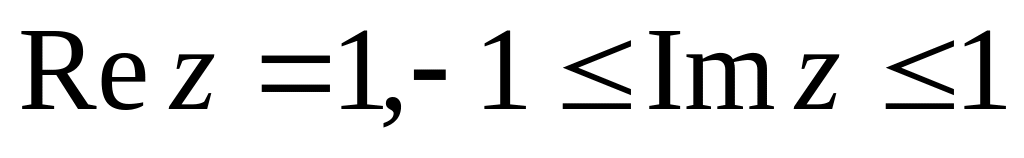Варіант 4

1. Знайти модуль і головне значення аргументу числа .

2. Знайти аналітичну функцію аргументу , уявна частина якої є .

3. Користуючись інтегральною формулою Коші, обчислити інтеграл 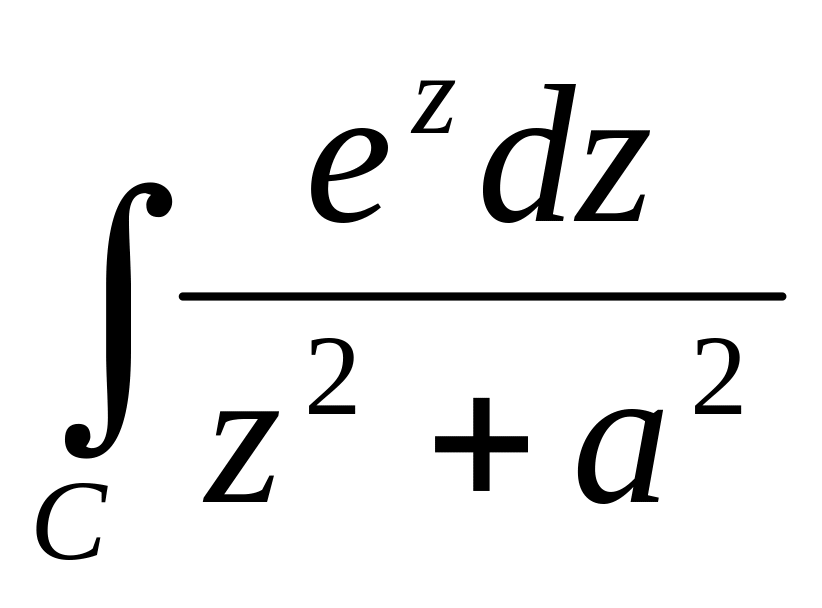, де С — коло .

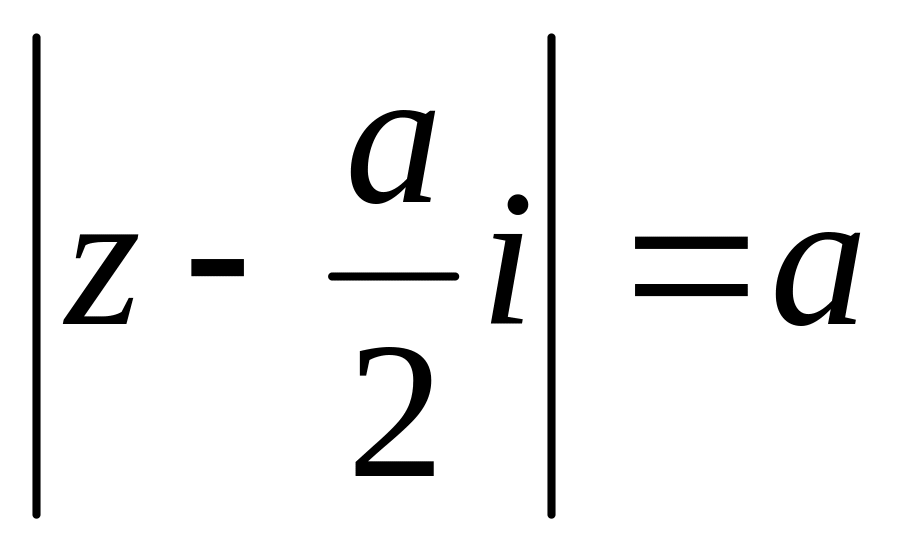4. Написати перші чотири члени розкладу в ряд Тей­лора в околі нульової точки функції 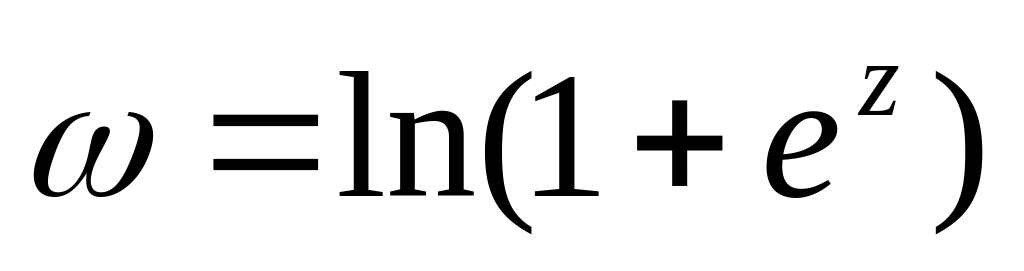і знайти радіус збіжності цього ряду.

5. Знайти всі особливі точки функції і обчислити лишки відносно всіх її полюсів.

6. На яку область перетворюється півкруг , 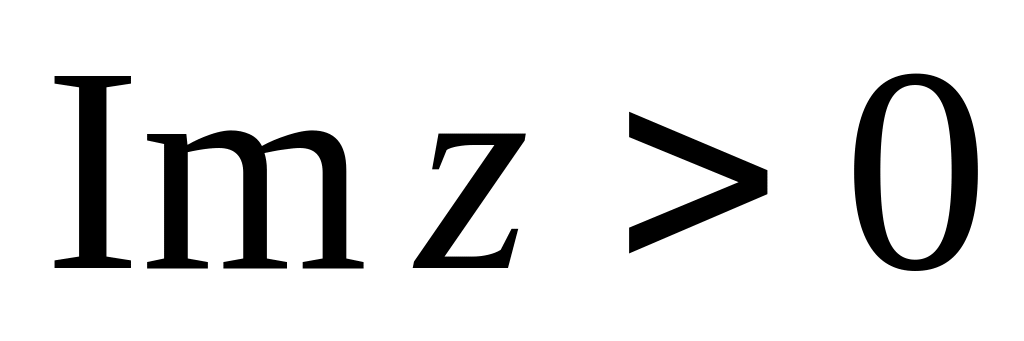за допомогою функції ?

Варіант 5

1. Знайти всі значення числа 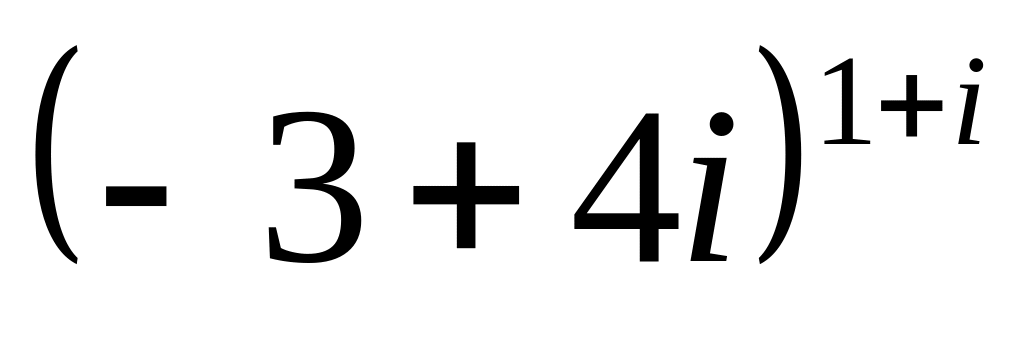і виділити головне значения.

2. Чи існує аналітична функція 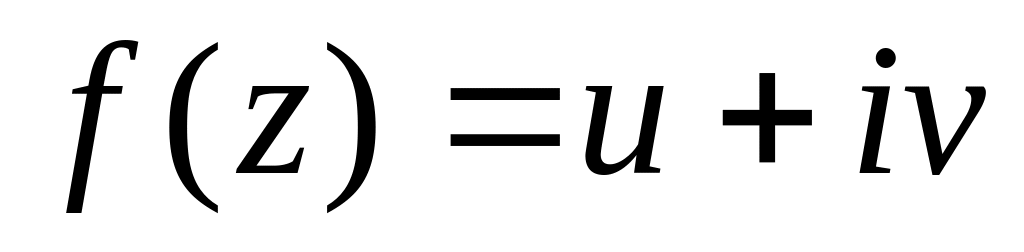, де , для якої ?

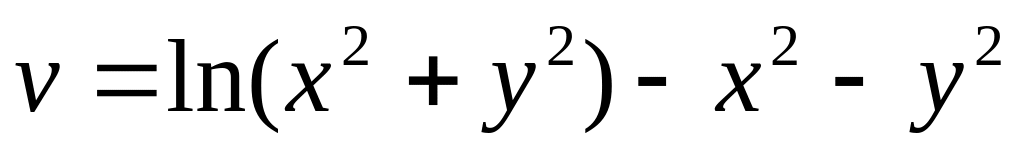3. Користуючись інтегральною формулою Коші, обчислити інтеграл , де С- еліпс .

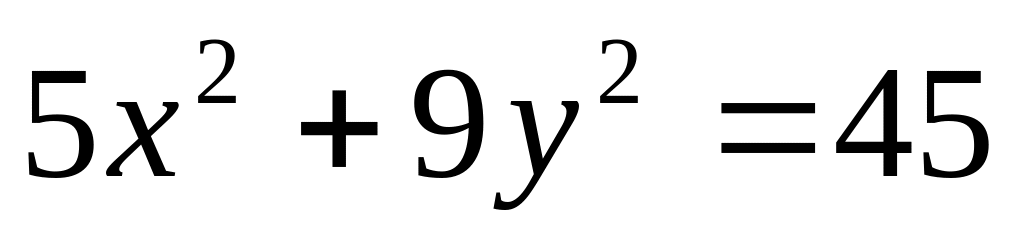4. Написати перші чотири члени розкладу в ряд Тей­лора в околі нульової точки функції 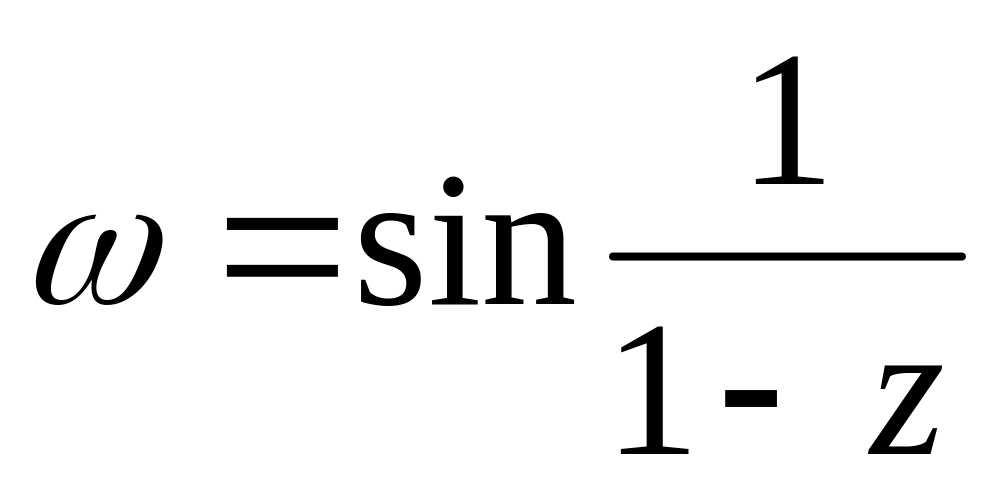і знай­ти радіус збіжності цього ряду.

5. Користуючись основною теоремою про лишки, об­числити інтеграл 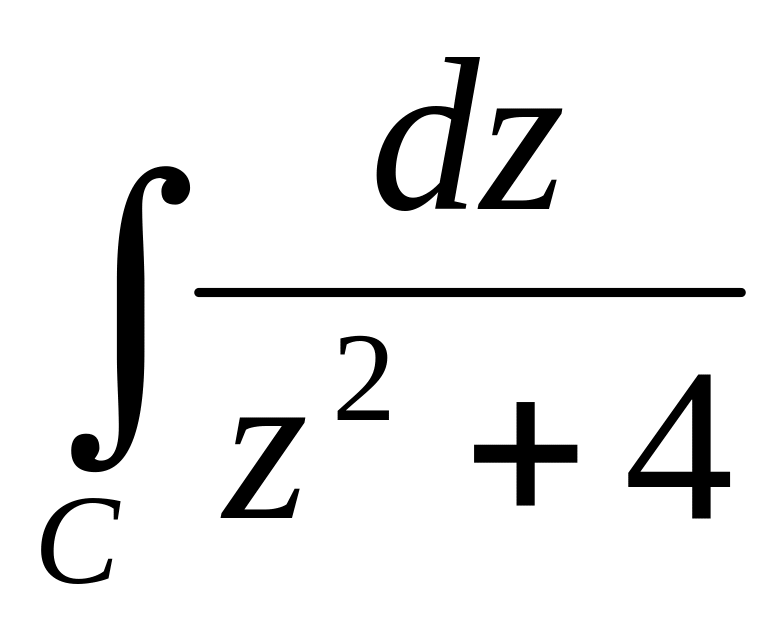С — коло .

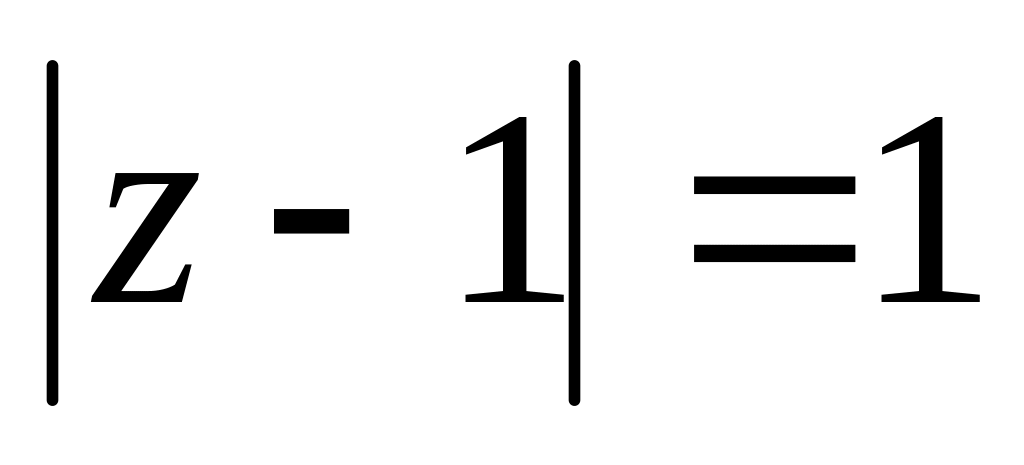6. Знайти функцію, яка відображає конформно і вза­ємно однозначно круг на нижню півплощину до так, що точки 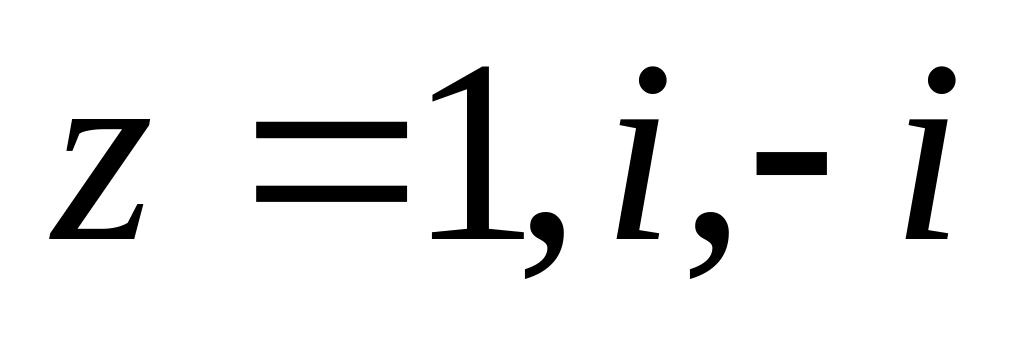переходять відповідно в точки: .

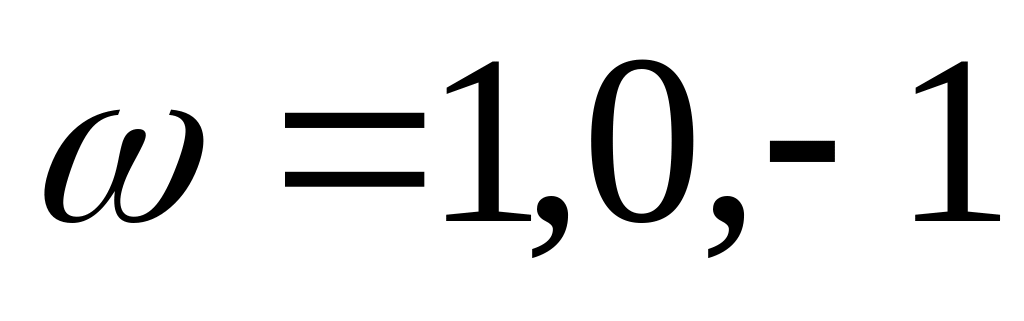Варіант 6

1. Накреслити графік функції , де х — дійсна змінна.

2. Чи існує аналітична функція , де , для якої ?

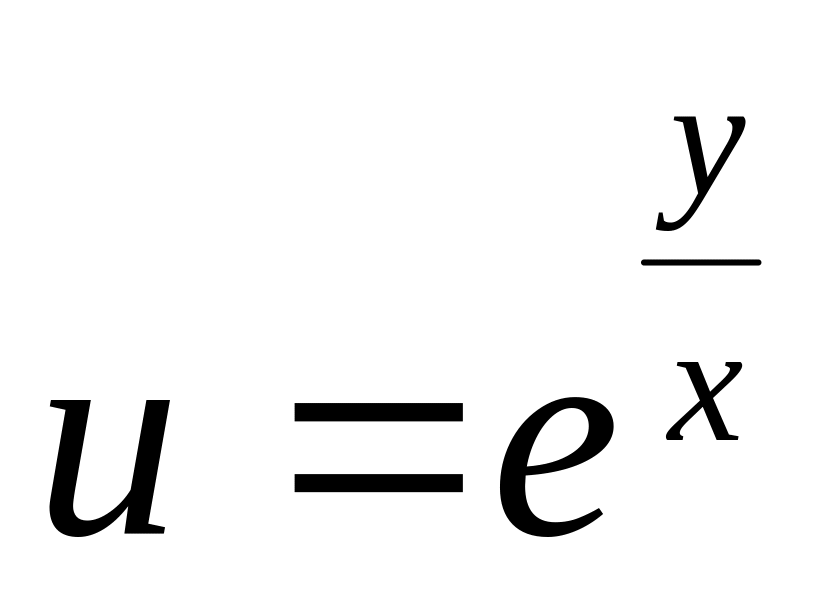3. Користуючись інтегральною формулою Коші, обчислити інтеграл , де С- коло .

4. Розкласти функцію в ряд Тейлора в околі нульової точки і знайти радіус збіжності цього ряду.

5. Користуючись основною теоремою про лишки, обчислити інтеграл 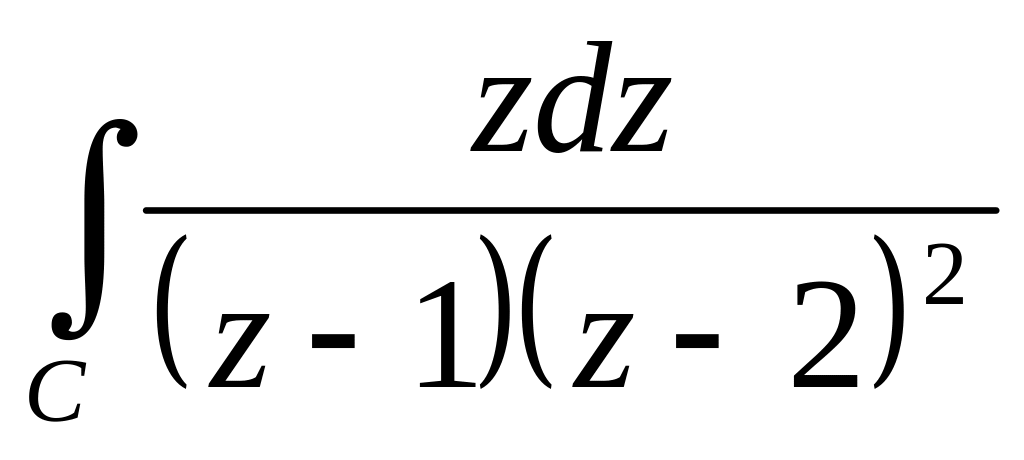, де С — коло .

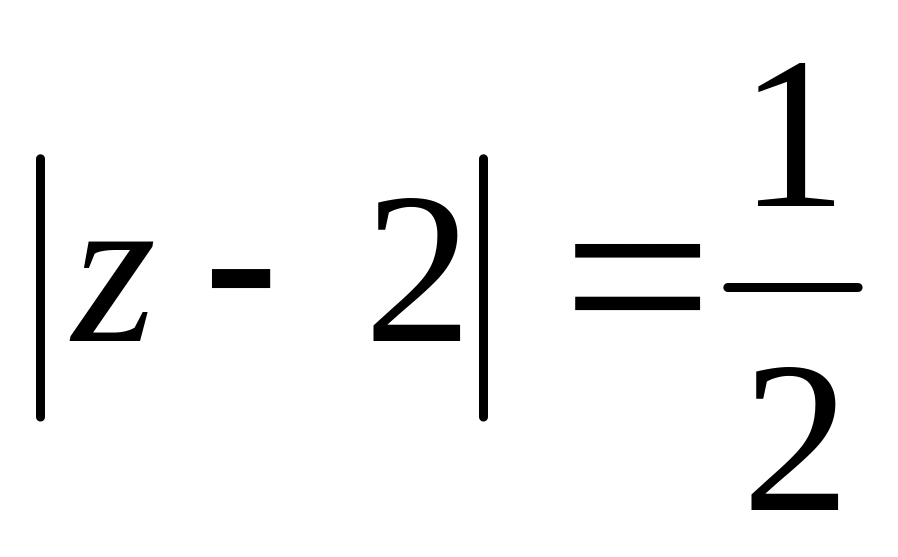6. Відобразити круг на півплощину 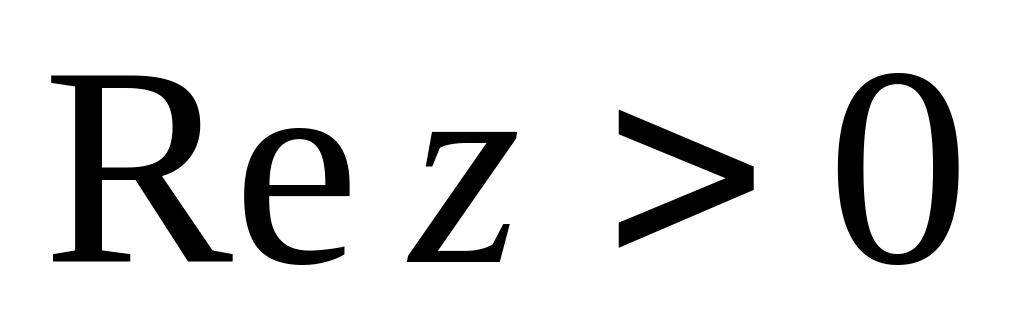так, щоб виконувались умови .

Варіант 7

1. Яка лінія задана рівнянням: 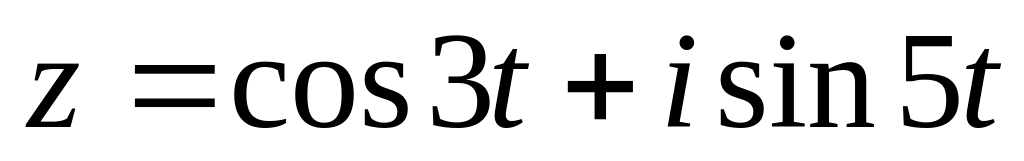, де t — дійсний параметр?

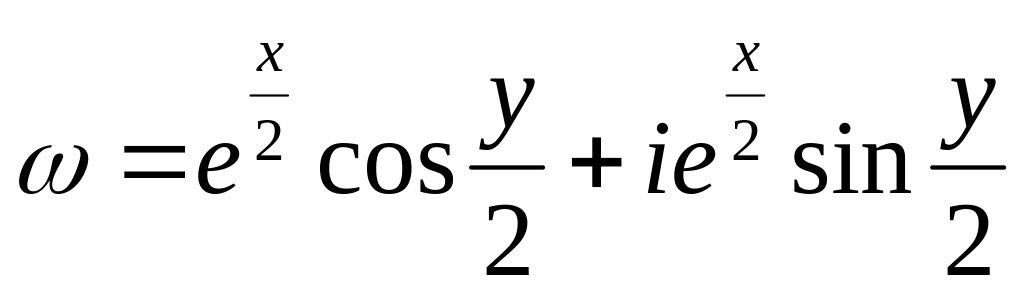2. Довести, що функція до є ана­літична на всій площині .

3. Користуючись інтегральною формулою Коші, обчислити інтеграл — прямокутник з вершинами в точках .

4. Розкласти у ряд Тейлора по степенях z функцію і визначити радіус збіжності цього ряду.

5. Користуючись основною теоремою про лишки, обчислити інтеграл 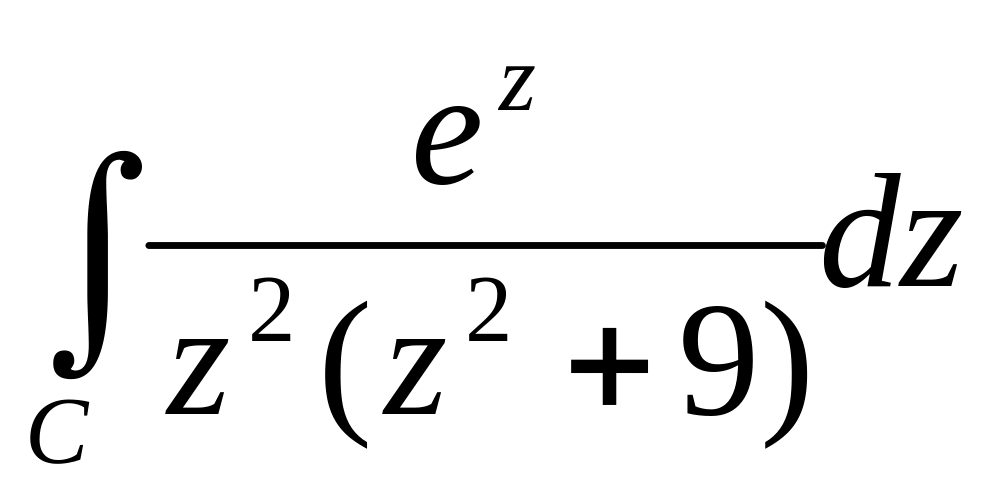С — коло .

6. З'ясувати, на що перетворюється при відображенні 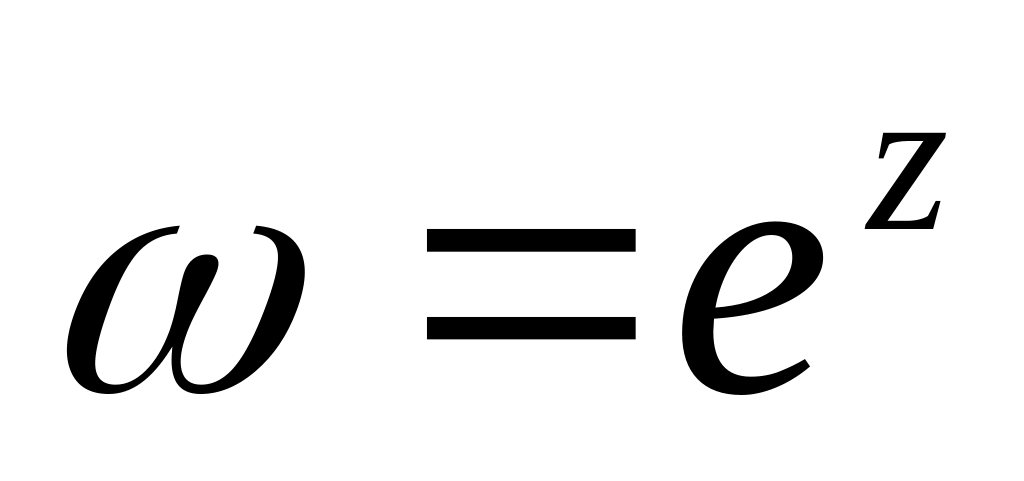смуга між прямими .

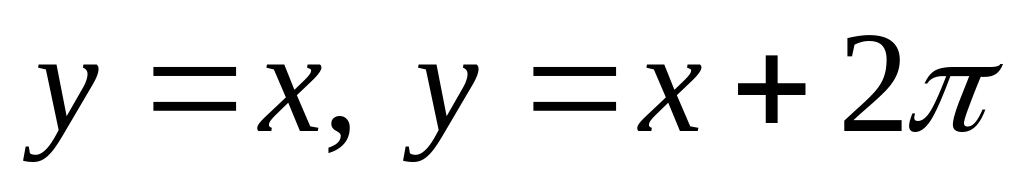Варіант 8

1. Яка лінія визначається рівнянням: ?

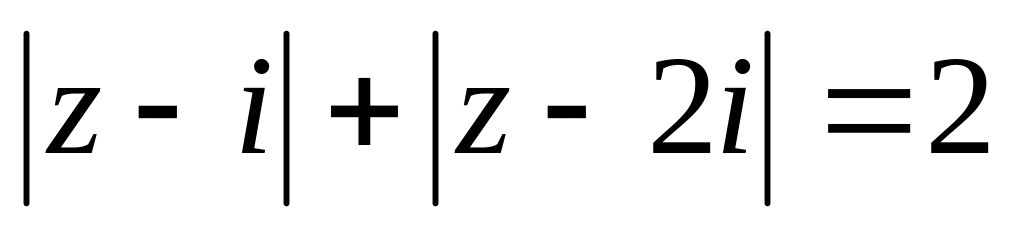2. Довести, що функція ( 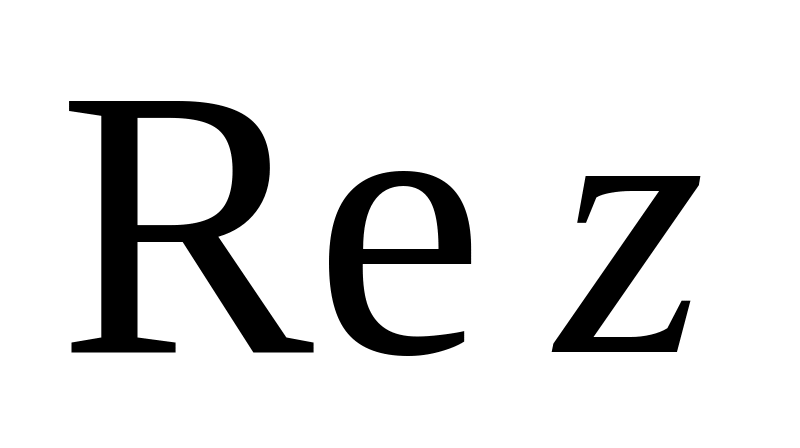— дійсна частина z) диференційовна лише в точці 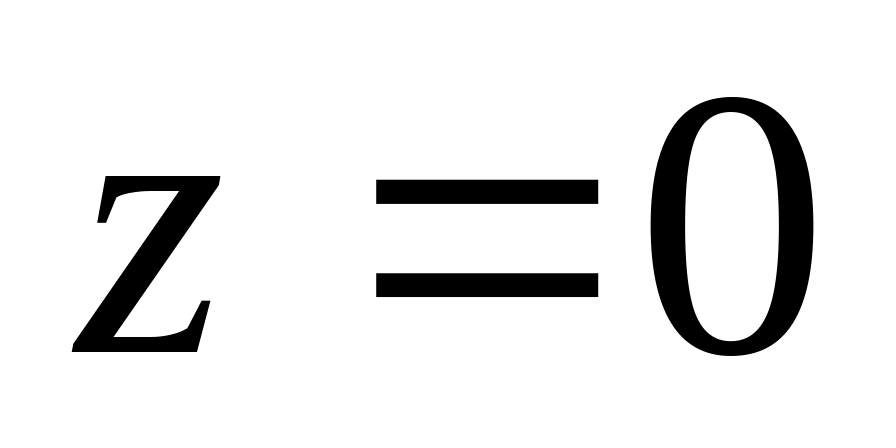. Знайти .

3. Виходячи з означення комплексного інтеграла, довести, що 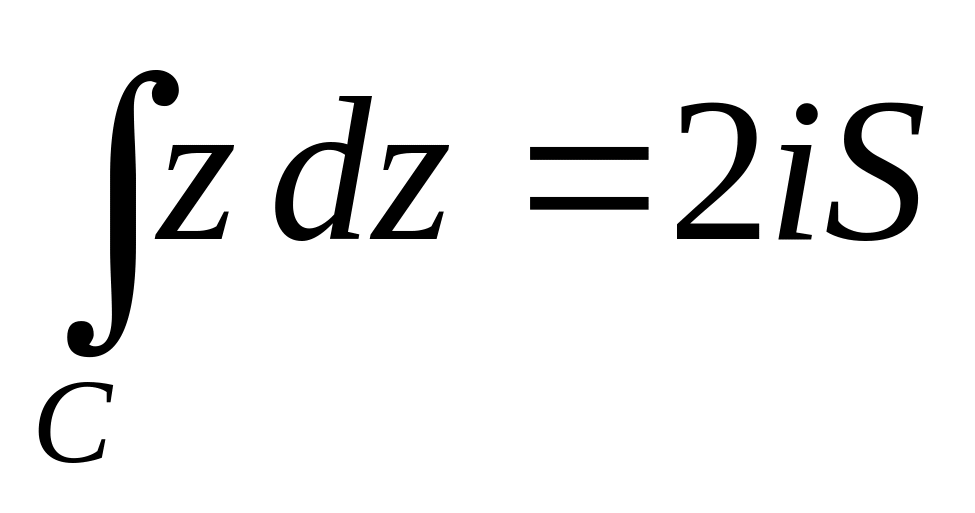, якщо С будь-який простий замкнутий контур, що обмежує область, площа якої дорівнює S.

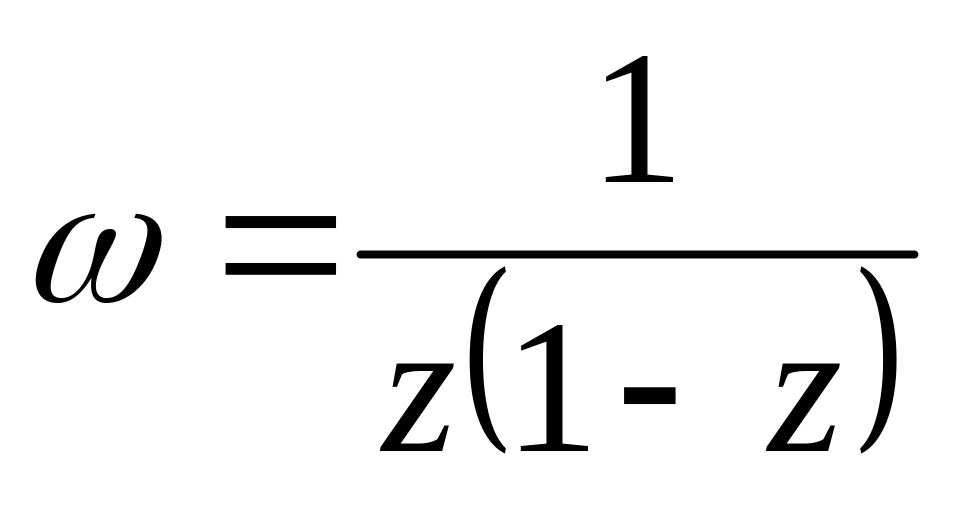4. Розкласти у ряд Лорана функцію в околі точки і вказати область, в якій цей розклад має місце.

5. Знайти усі особливі точки функції і визначити їх характер.

6. Знайти функцію, яка перетворює конформно круг в себе так, що точки –1, і, 1 переходять відповідно в точки .

Варіант 9

1. Розв'язати рівняння: .

2. Довести, що функція не має похідної в жодній точці комплексної площини z.

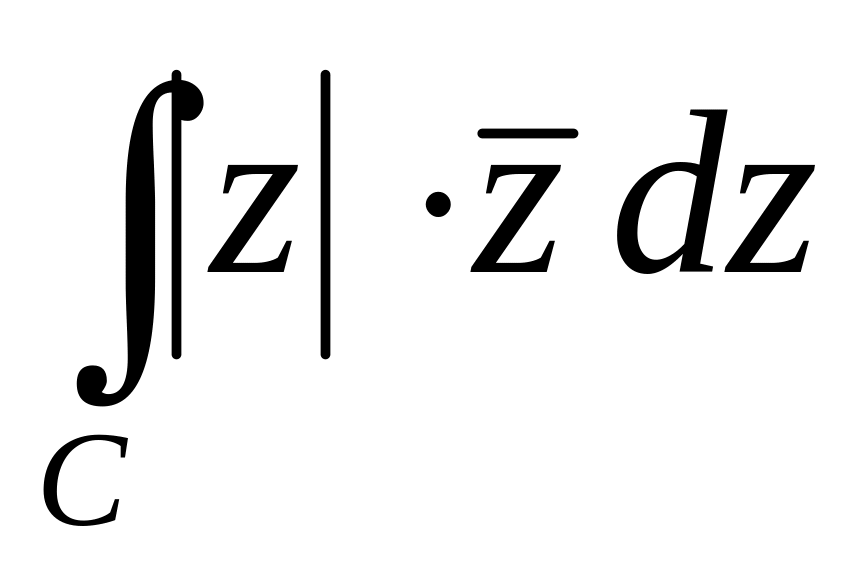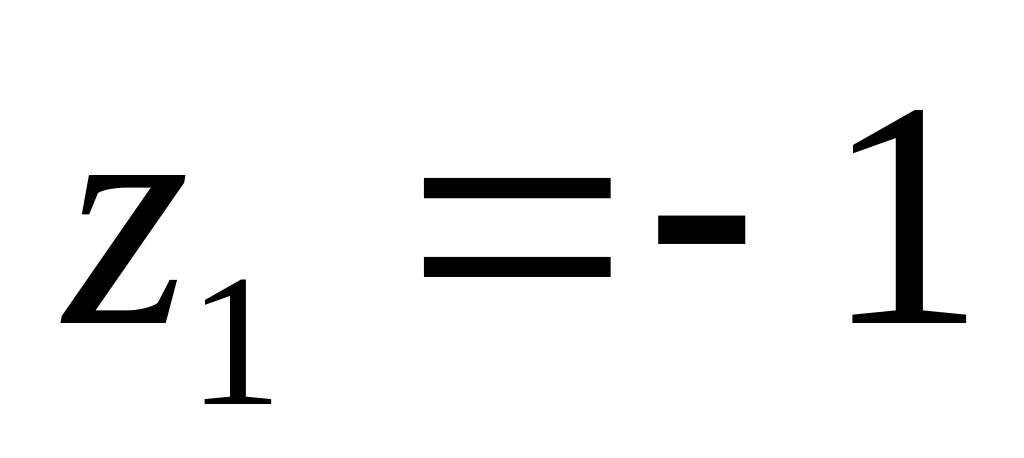3. Обчислити , де С є замкнутий контур, який складається з верхнього півкола і відрізка осі від до .

4. Розкласти у ряд Лорана функцію 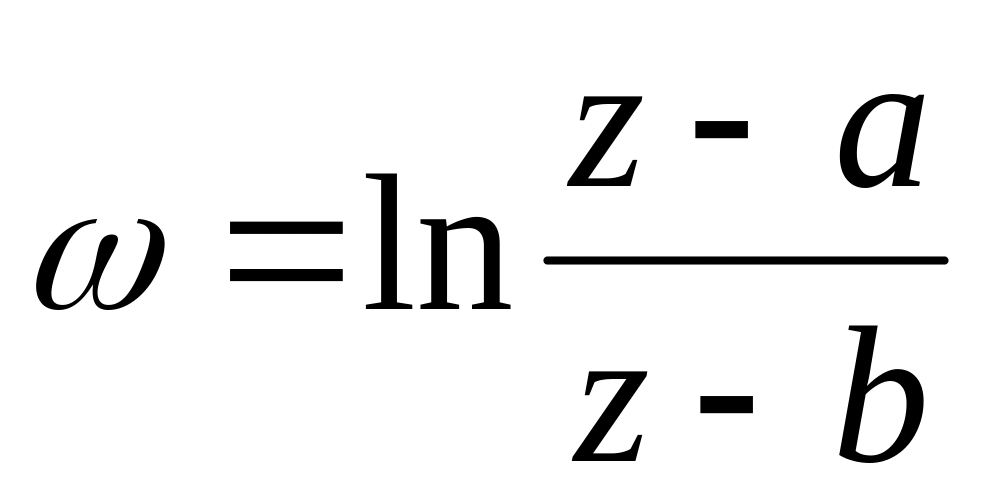в околі точки

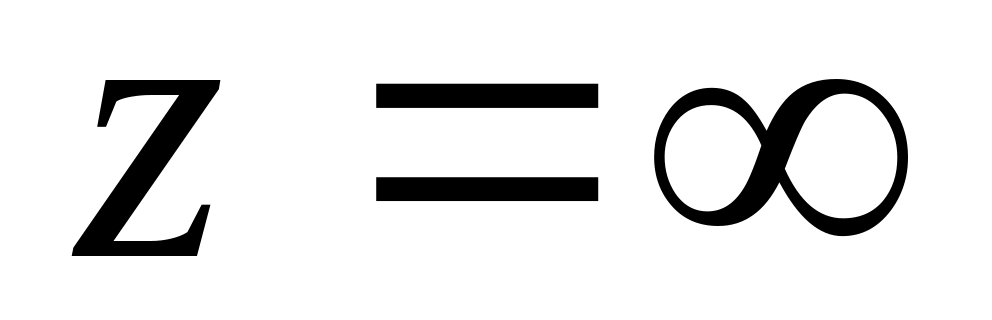
5. Знайти усі особливі точки функції і визначити їх характер.

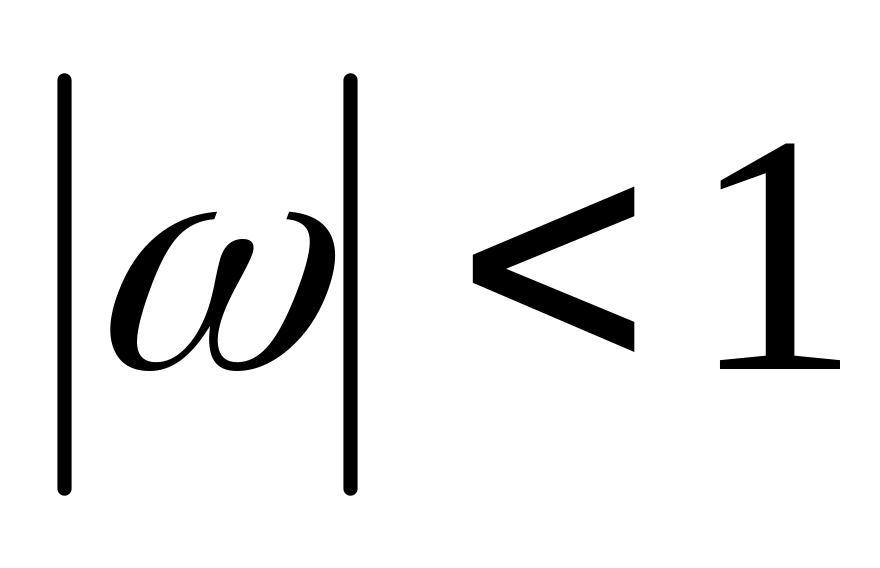6. Відобразити круг на круг так, щоб точка відобразилась в точку 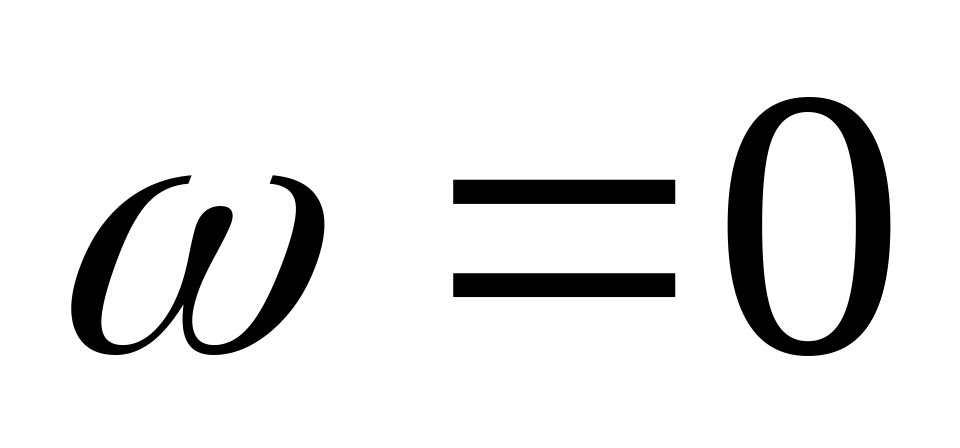і щоб мала місце рівність .

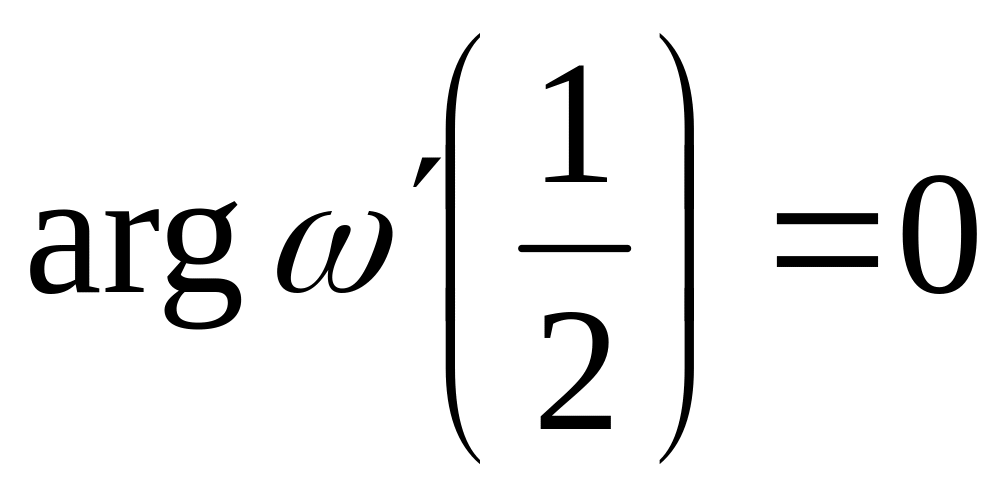Варіант 10

1. Розв'язати рівняння: .

2. З'ясувати, яка частина площини z стискується і яка розтягається, якщо відображення здійснює функція .

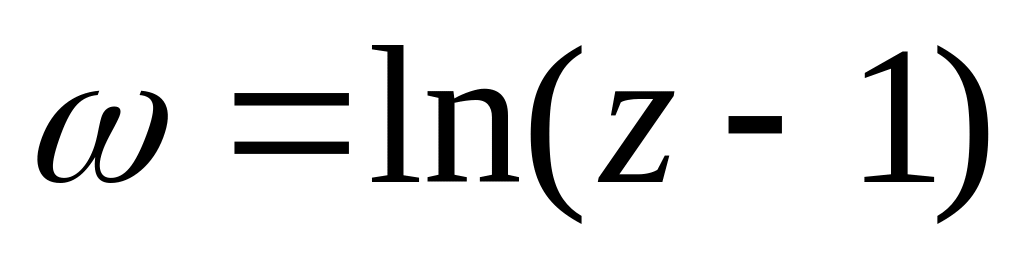3. Обчислити всі можливі значення 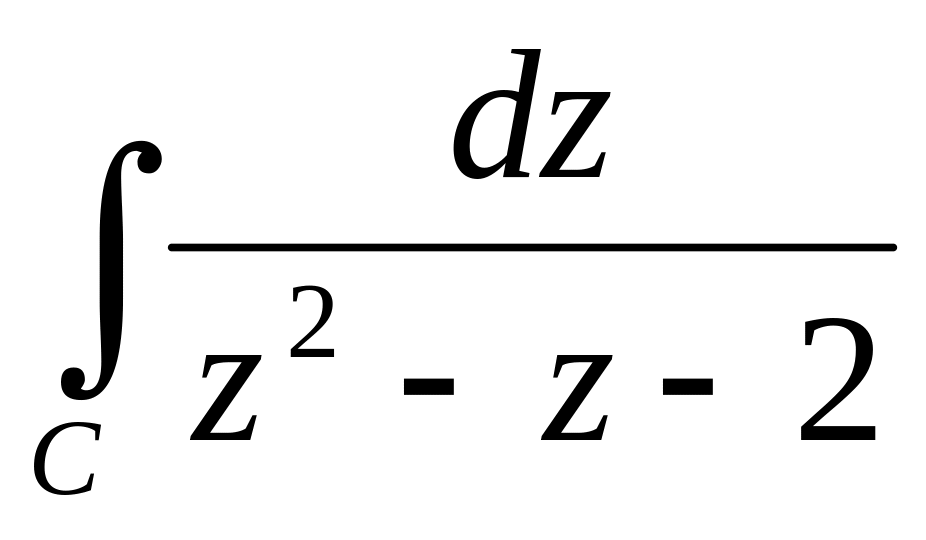при різних положеннях контура С, який не проходить через точки .

4. Розкласти у ряд Лорана функцію 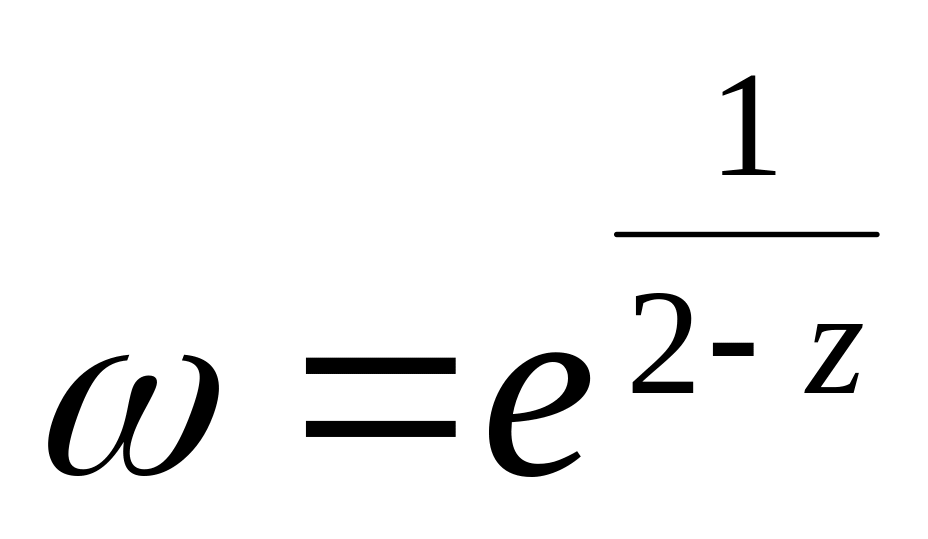в околі точки .

5. Чи існує функція, аналітична в точці , яка набирає в точках 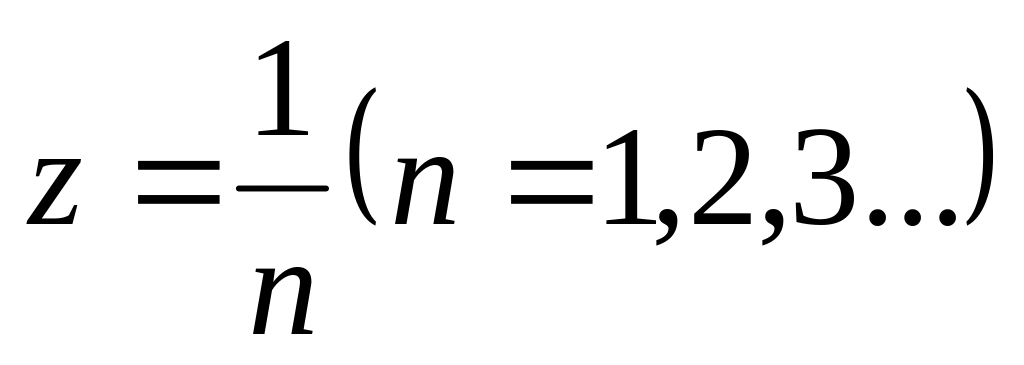відповідно значення: ?

6. З'ясувати, на що перетворюється при відображенні 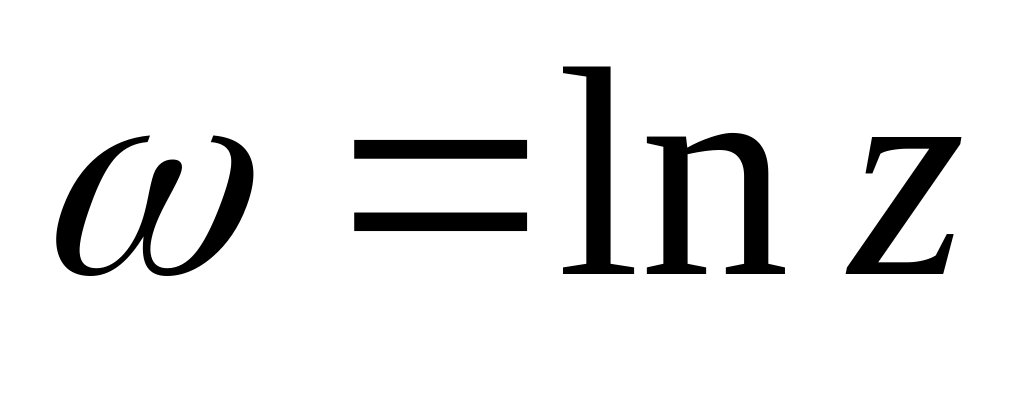кут .