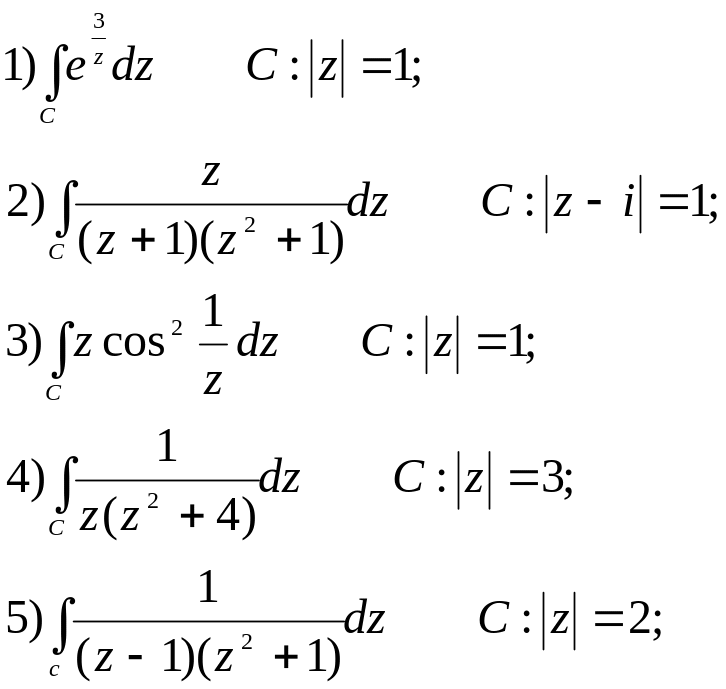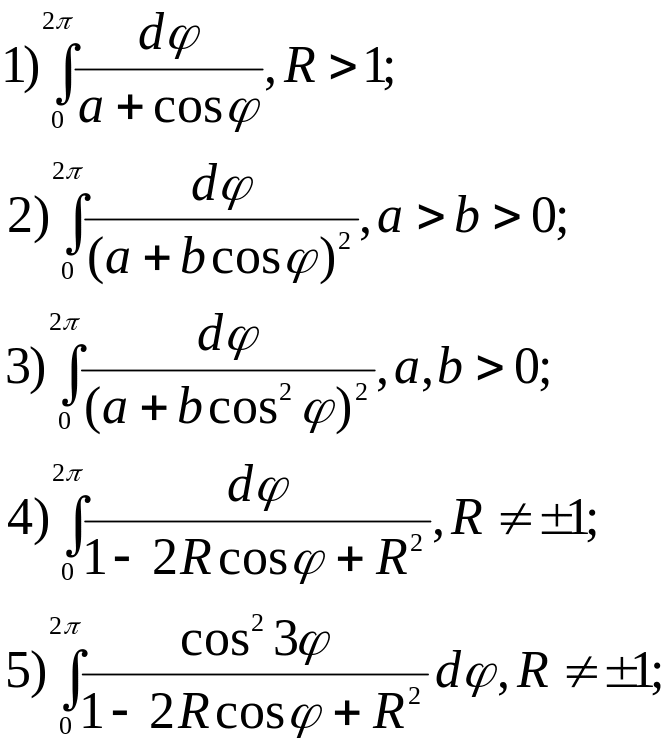- •Змістовний модуль №1. Комплексні числа та їх геометричне представлення
- •Комплексні числа. Форми запису комплексного числа. Дії над комплексними числами
- •1.2. Послідовності і ряди комплексних чисел. Степеневий ряд
- •Змістовний модуль №2. Похідна функції комплексної змінної
- •2.1 Функції із с в с. Границя, неперервність
- •2.2. Похідна функції комплексної змінної. Умови диференційованості
- •2.3. Геометричний зміст модуля і аргументи похідної комплексної функції
- •2.4. Означення аналітичної функції. Поняття Конформного відображення
- •Змістовний модуль №3. Елементарні аналітичні функції
- •Лінійна функція
- •Дробово-лінійна функція
- •Степенева функція. Поверхня Рімана
- •Функція Жуковского
- •Показникова функція комплексної змінної
- •Тригонометричні функції
- •Логарифмічна функція. Точка розгалуження
- •Радикал. Загальна степенева функція
- •Обернені тригонометричні функції
- •Змістовний модуль №4. Інтеграл функції комплексної змінної
- •Інтеграл від функції комплексної зміної по кусочно-гладкому контуру
- •Теорема Коші
- •Невизначений інтеграл. Формула Ньютона-Лейбница
- •Змістовний модуль № 5. Інтегральна формула Коші та її наслідки
- •5.1. Формула Коші. Принцип максимума модуля
- •5.2. Цілі функції. Теорема Ліувіля. Основна теорема алгебри
- •5.3. Розкладання функції в ряд Тейлора. Оцінка коефіцієнтів степеневого ряду
- •5.4. Нулі аналітичної функції. Ізольованість нулів. Теорема єдиності
- •5.5. Аналітичне продовження. Елементарні функції як аналітичні продовження
- •Змістовний модуль № 6. Ізольовані особливі точки аналітичних функцій
- •6.1. Розкладання аналітичної функції в ряд Лорана
- •6.2. Класифікація ізольованих особливих точок. Нескінченно віддалена особлива точка. Критерій особливої точки, яка усувається
- •6.3. Критерій полюса
- •6.4. Теорема Сохоцького-Вейєрштрасса
- •6.5. Раціональні і міроморфні функції
- •Змістовний модуль № 7. Лишки та їх застосування
- •7.1. Означення ЛишкА. Обчислення лишків
- •7.2. Основна теорема теорії лишків
- •7.3. Застосування теореми лишків до обчислення визначених інтегралів
- •Контрольні роботи Контрольна робота №1 (денна форма навчання)
- •Контрольна робота №2 (денна форма навчання)
- •Контрольна робота (заочна форма навчання)
- •Зразки розв'язування задач
- •Література
Змістовний модуль № 7. Лишки та їх застосування
7.1. Означення ЛишкА. Обчислення лишків
Нехай – ізольована особлива точка функції , тоді в розкладі в ряд Лорана функції в точці коефіцієнт
![]() ,
,
де С – довільний замкнутий контур, що містить в середині себе єдину особливу точку функції і обходиться в додатному напрямі.
Означення1. Лишком в ізольованій особливій точці називається комплексне число, що дорівнює .
Позначається
цей факт, як
![]() .
.
Можливі наступні можливості:
1)
-
особлива точка, яка усувається, тоді
![]() ;
;
2)
- полюс першого порядку
,
тоді![]()
![]() ,
тобто
,
тобто
![]() .
.
Приклад1.
![]() .
Тоді
-
полюс першого порядку
.
Тоді
-
полюс першого порядку
![]() .
.
3)
– полюс
![]() -го
порядку, тоді
-го
порядку, тоді
![]()
і
![]() .
.
Приклад2.
![]() .
Тоді
.
Тоді
![]() -
особлива; полюс другого порядку, тобто
m=2.
-
особлива; полюс другого порядку, тобто
m=2.
![]()
Вправи
Обчислити:
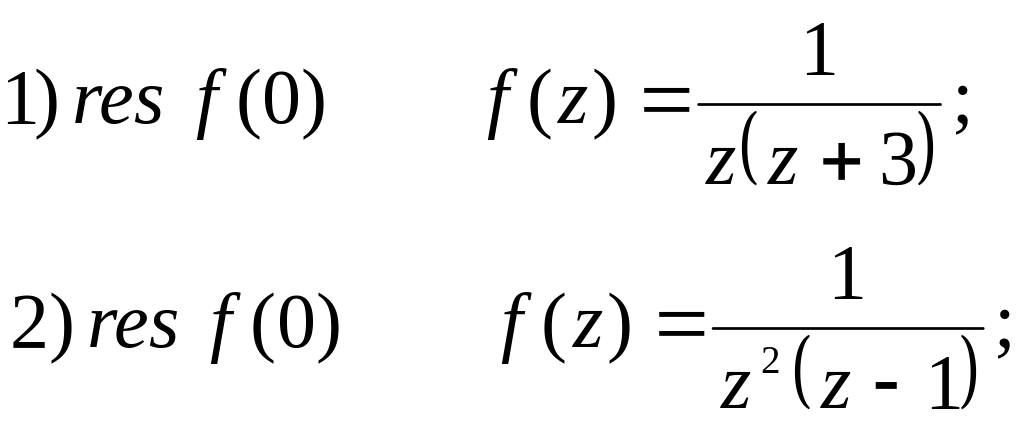
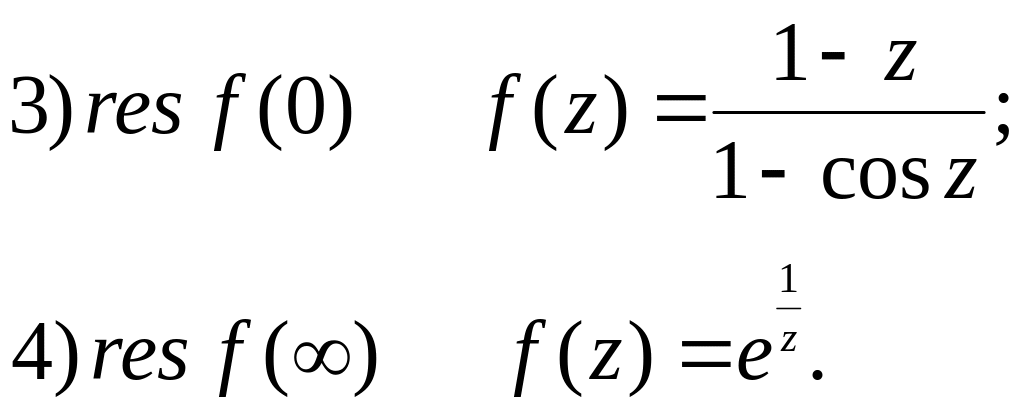
Знайти лишки по всім особливим точкам:
|
|
7.2. Основна теорема теорії лишків
Теорема1.
Нехай
аналітична функція в замкненій області
за виключенням скінченого числа
ізольованих особливих точок
![]() ,
що лежать в середині
,
тоді
,
що лежать в середині
,
тоді
![]() ,
,
де С – повна границя області , що проходить в додатному напрямі.
Доведення теореми див. [2, с.305], [1, с.122].
Приклад1.
![]() .
.
Оскільки
![]() має дві особливі ізольовані точки
має дві особливі ізольовані точки
![]() ,
що лежать в середині контуру С,
то
,
що лежать в середині контуру С,
то ![]()
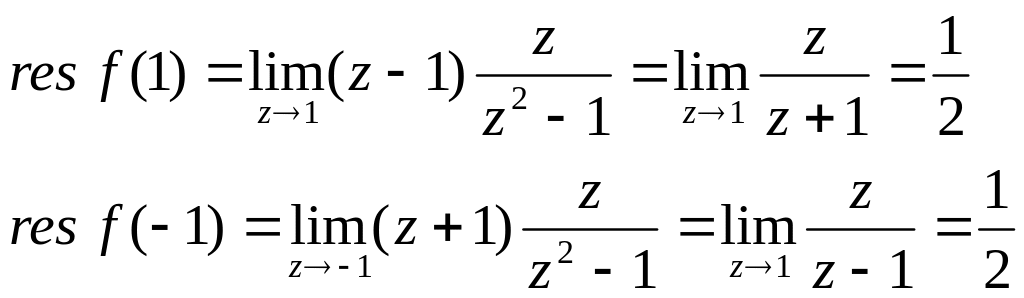
Таким
чином,
![]() .
.
Вправи
Обчислити:
|
|
![]()
7.3. Застосування теореми лишків до обчислення визначених інтегралів
Розглянемо
![]() ,
де R – раціональна функція своїх
аргументів, тоді вірна формула:
,
де R – раціональна функція своїх
аргументів, тоді вірна формула:
![]() ,
дійсно після заміни
,
дійсно після заміни
![]()
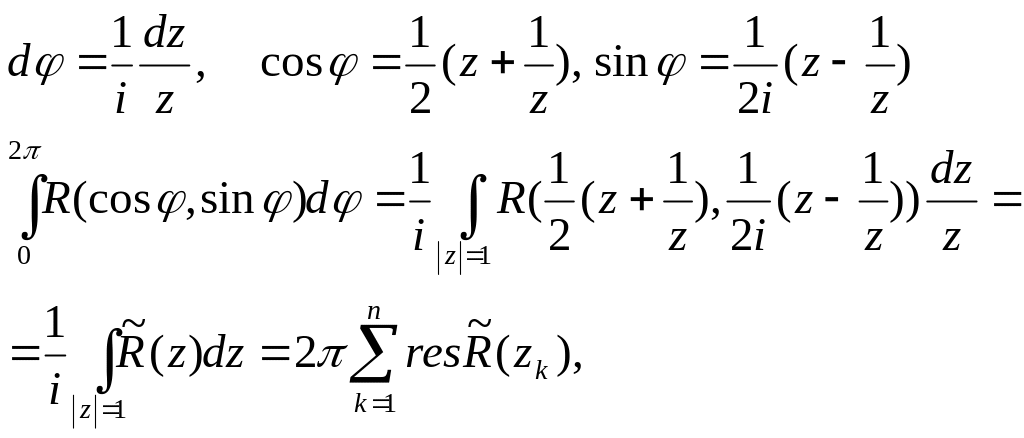
де
![]() – особлива точка
– особлива точка
![]() ,
що міститься в середині
,
що міститься в середині
![]() .
.
Приклад1.
![]()
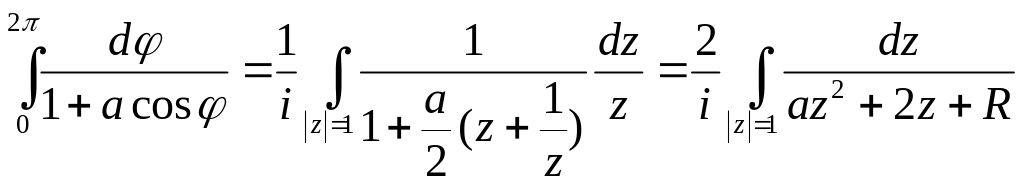
Особливі точки функції
![]() .
.
Точки
![]() – полюси першого порядку, але в середині
знаходиться тільки точка
– полюси першого порядку, але в середині
знаходиться тільки точка
![]() .
Тому
.
Тому
![]()
![]()
Теорема2.
Нехай
функція
задана на всій дійсній осі
![]() ,
може бути аналітично продовжена на
верхню півплощину
,
може бути аналітично продовжена на
верхню півплощину
![]() ,
причому її аналітичне продовження,
,
задовольняє умовам:
,
причому її аналітичне продовження,
,
задовольняє умовам:
Існують числа
 ,
для всіх z з верхньої півплощини таких,
що
,
для всіх z з верхньої півплощини таких,
що
 виконується оцінка
виконується оцінка
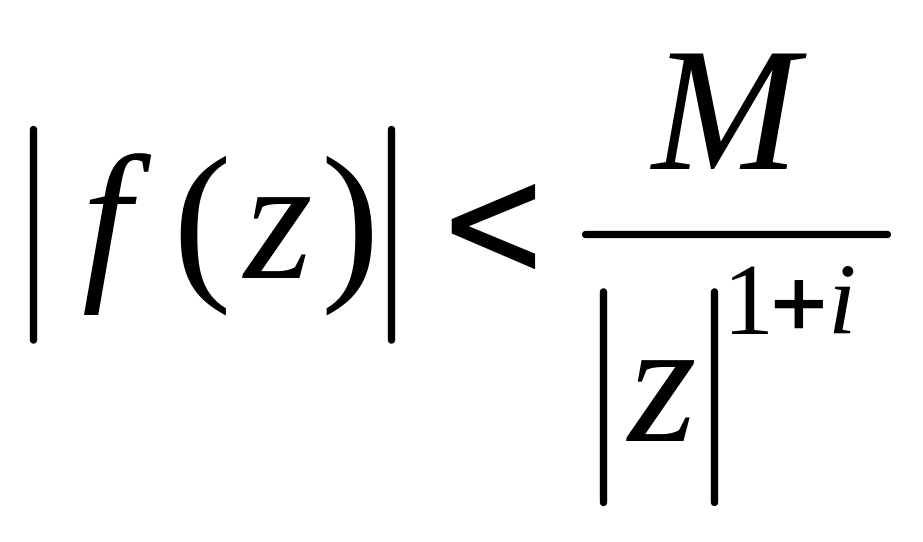 ;
;не має особливих точок на дійсній осі, а в півплощині має не більше скінченого числа ізольованих особливих точок.
Тоді
![]() ,
де
,
де
![]() -
особлива точка
в верхній півплощині.
-
особлива точка
в верхній півплощині.
Доведення теореми див. [1, с. 127].
Приклад2.
![]() .
Тоді
.
Тоді
![]() -
задовольняє умовам теореми. Особливі
точки в верхній півплощині
-
задовольняє умовам теореми. Особливі
точки в верхній півплощині
![]() причому обидві – полюси першого порядку.
Тому
причому обидві – полюси першого порядку.
Тому
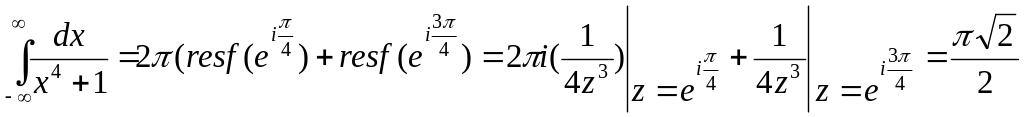
Вправи
Обчислити.
|
|
Контрольні роботи Контрольна робота №1 (денна форма навчання)
Варіант 1
1. Використовуючи
умову Коші-Римана, довести, що
![]() диференційована в комплексній площині
і знайти
диференційована в комплексній площині
і знайти
![]() ,
якщо
,
якщо
![]() .
.
2. Нехай
![]() ,
знайти образи областей:
,
знайти образи областей:
![]() і
і
![]() .
.
3. Нехай
![]() .
Знайти образ області:
.
Знайти образ області:
![]() .
.
4. Нехай
![]() – багатозначна функція. Знайти образ
області
– багатозначна функція. Знайти образ
області
![]() ,
якщо
,
якщо
![]() .
.
5. Обчислити:
![]() ;
;
![]() ;
;
![]() .
.
6. Чи є
функція
![]() аналітичною?
аналітичною?
Варіант 2
1. Нехай
![]() – аналітична функція. Знайти її, якщо
– аналітична функція. Знайти її, якщо
![]() ,
,
![]() .
.
2. Знайти
дробово-лінійну функцію і образ області
![]() ,
якщо
,
якщо
![]() ,
,
![]() ,
,
![]() .
.
3. Знайти
образ області
при відображенні
![]() ,
якщо
,
якщо
![]() .
.
4. Знайти
образ області
при відображенні віткою багатозначної
функції
,
якщо
![]() ,
,
![]() .
.
5. Обчислити:
![]() ;
;
![]() ;
;
![]() .
.
6. Чи є
функція
![]() аналітичною?
аналітичною?
Варіант 3
1. Використовуючи умову Коші-Римана, довести, що диференційована в комплексній площині і знайти , якщо .
2. Нехай
![]() ,
знайти образи областей:
і
.
,
знайти образи областей:
і
.
3. Нехай
![]() .
Знайти образ області:
.
Знайти образ області:
![]() .
.
4. Нехай – багатозначна функція. Знайти образ області , якщо .
5. Обчислити:
![]() ;
;
![]() ;
;
![]() .
.
6. Чи є
аналітичною функція
![]() ?
?
Варіант 4
Нехай – аналітична функція. Знайти її, якщо
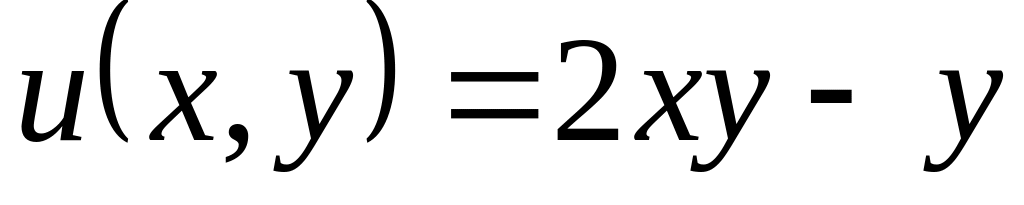 і
.
і
.Знайти дробово-лінійну функцію і образ області , якщо , , .
Знайти образ області при відображенні
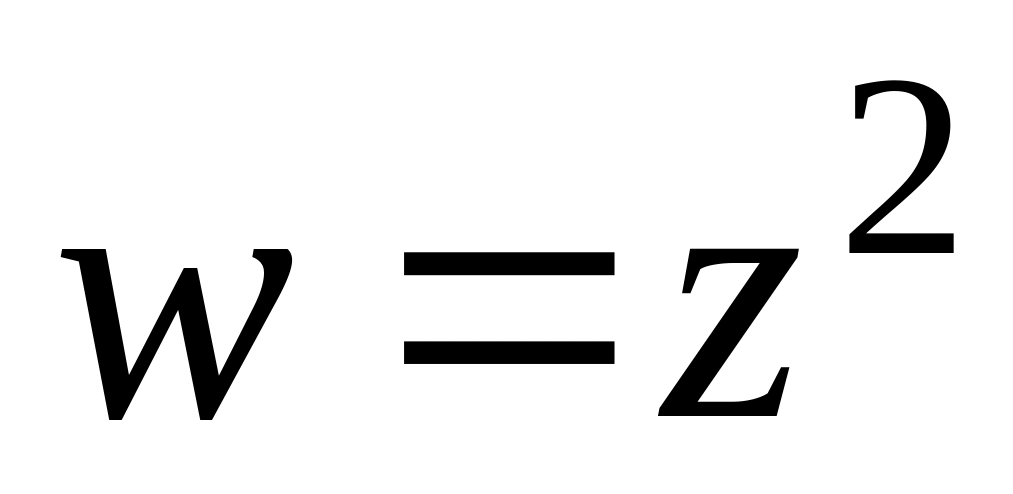 ,
якщо
,
якщо
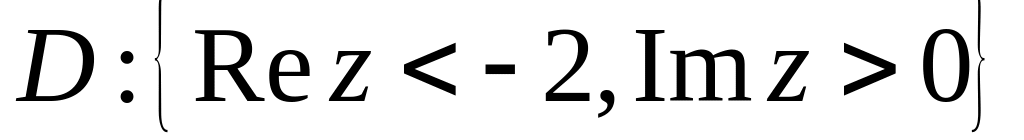 .
.Знайти образ області при відображенні віткою багатозначної функції , якщо
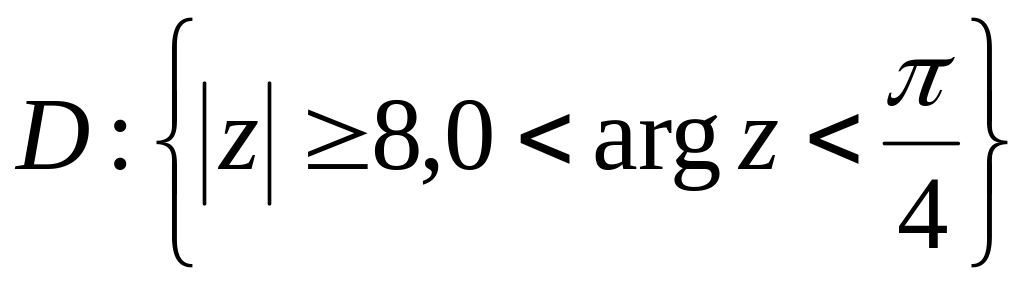 ,
.
,
.Обчислити:
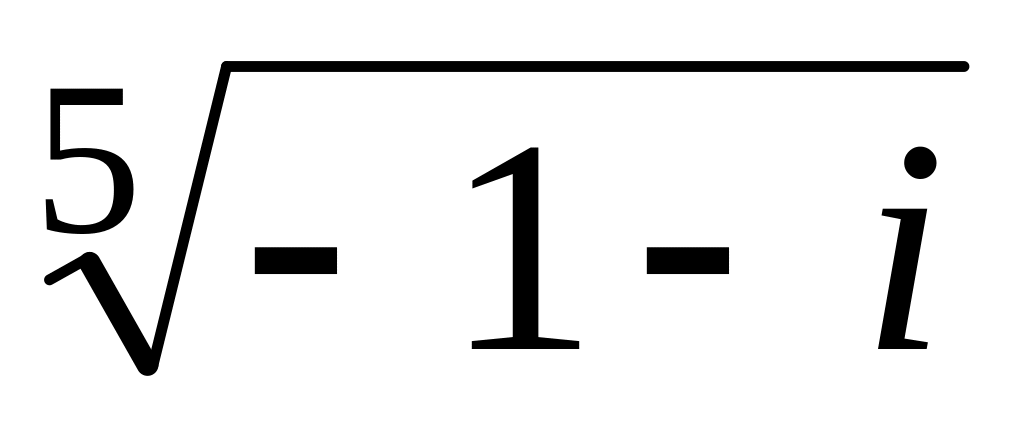 ;
;
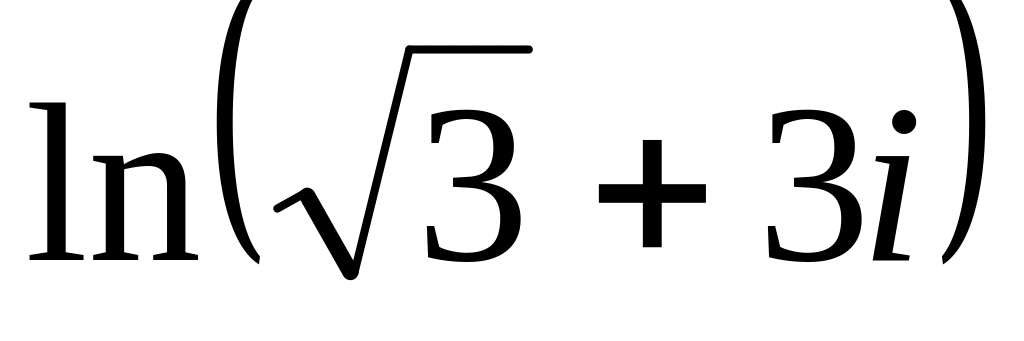 ;
;
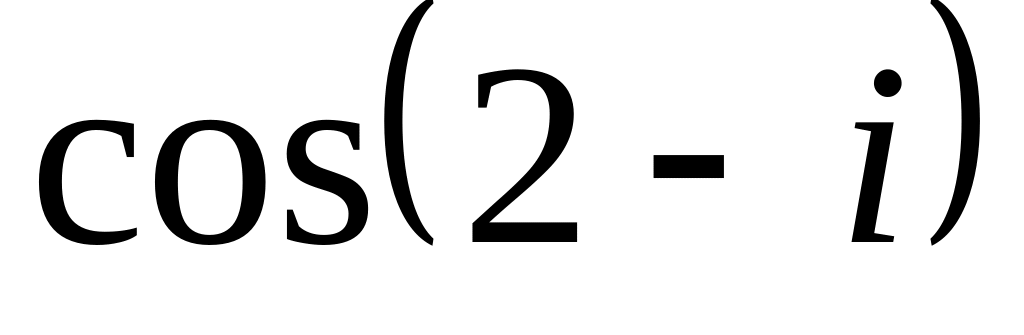 .
.
Чи є функція
 аналітичною?
аналітичною?
Варіант 5
Нехай – аналітична функція. Знайти її, якщо
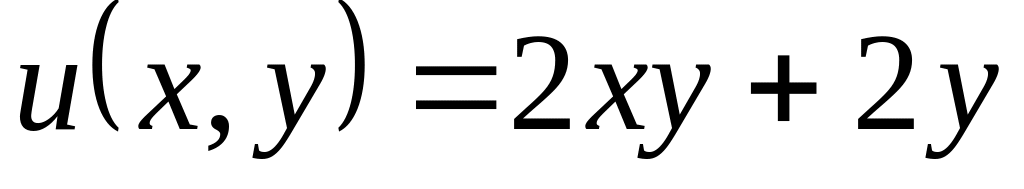 .
.Нехай . Знайти образи областей
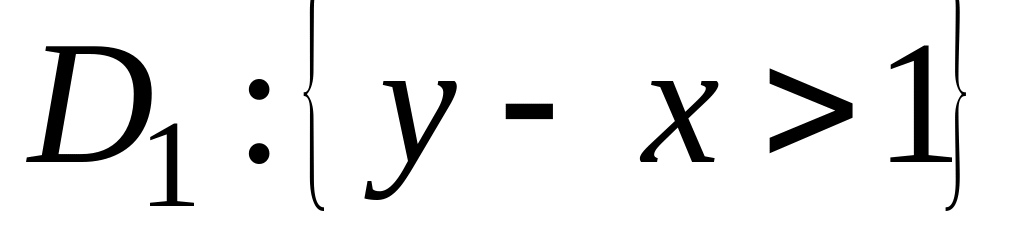 і
і
 .
.Знайти образ області
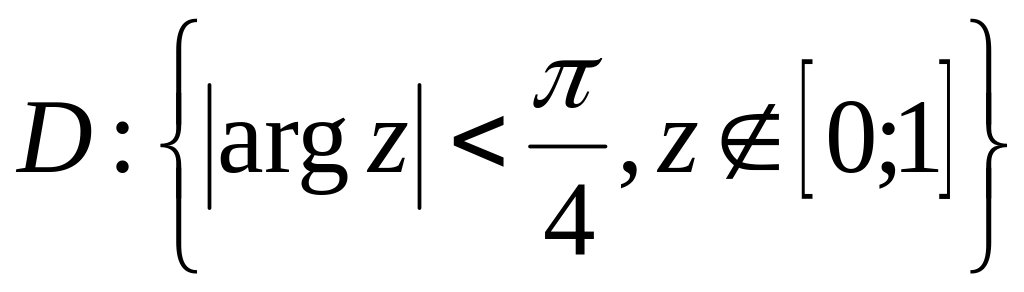 ,
якщо
,
якщо
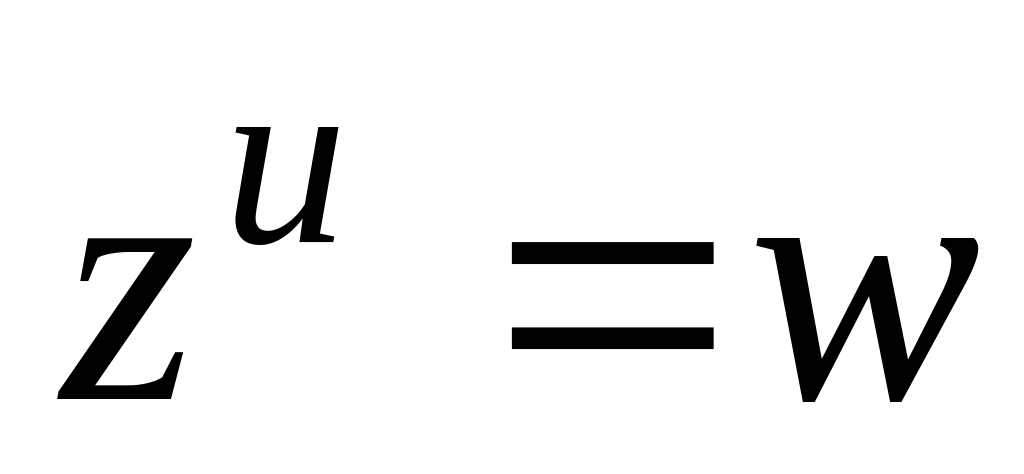 .
.Нехай – багатозначна функція. Знайти образ області
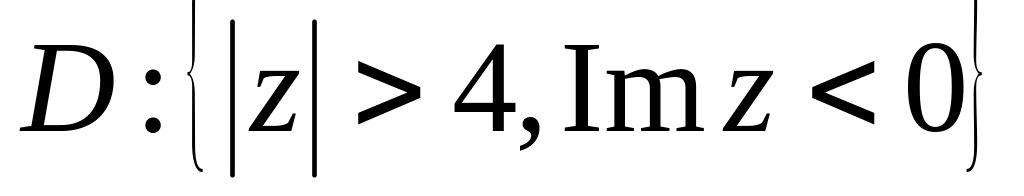 ,
якщо
.
,
якщо
.Обчислити:
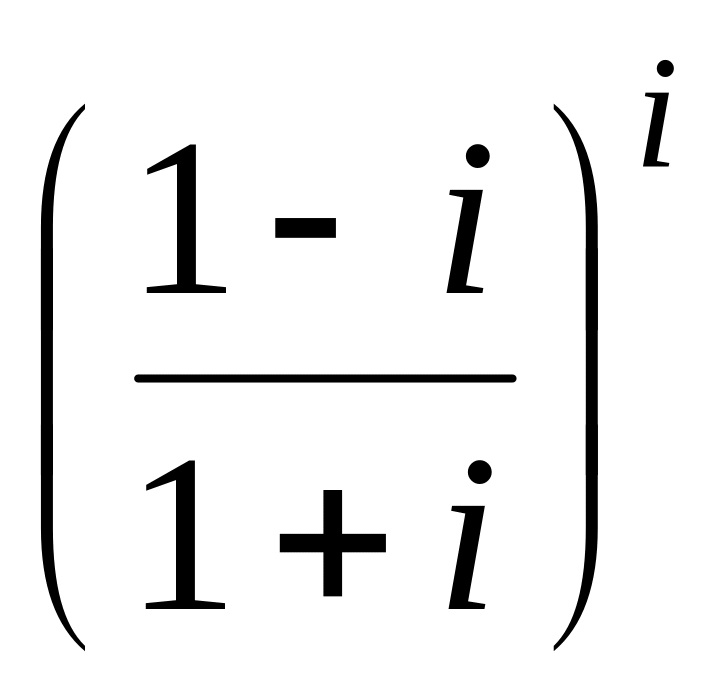 ;
;
;
;
 .
.Чи є аналітичною функція
 ?
?
Варіант 6
При якому значенні

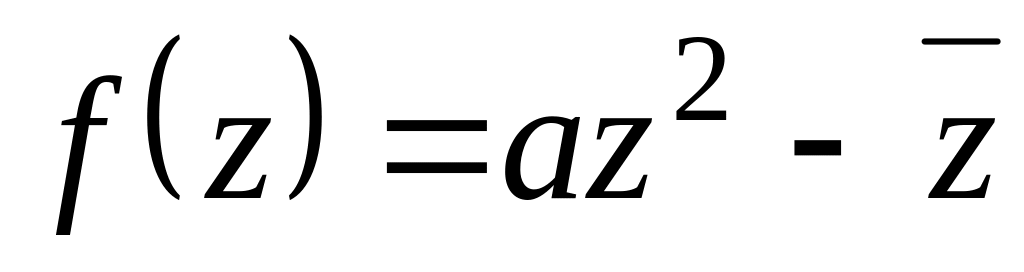 диференційована у всій комплексній
площині?
диференційована у всій комплексній
площині?Знайти дробово-лінійну функцію і образ області
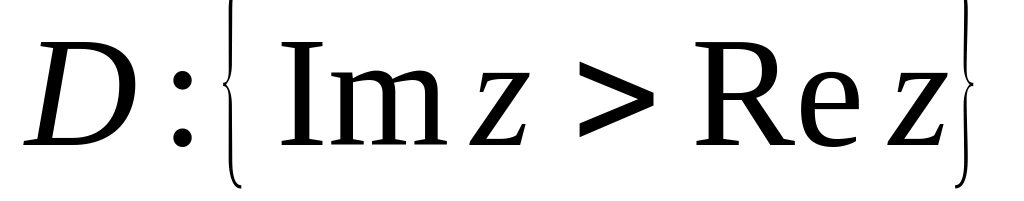 ,
якщо
,
якщо
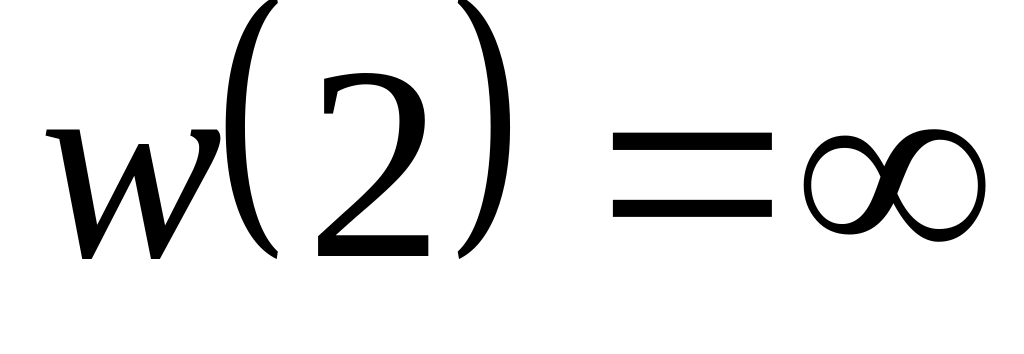 ,
,
 ,
,
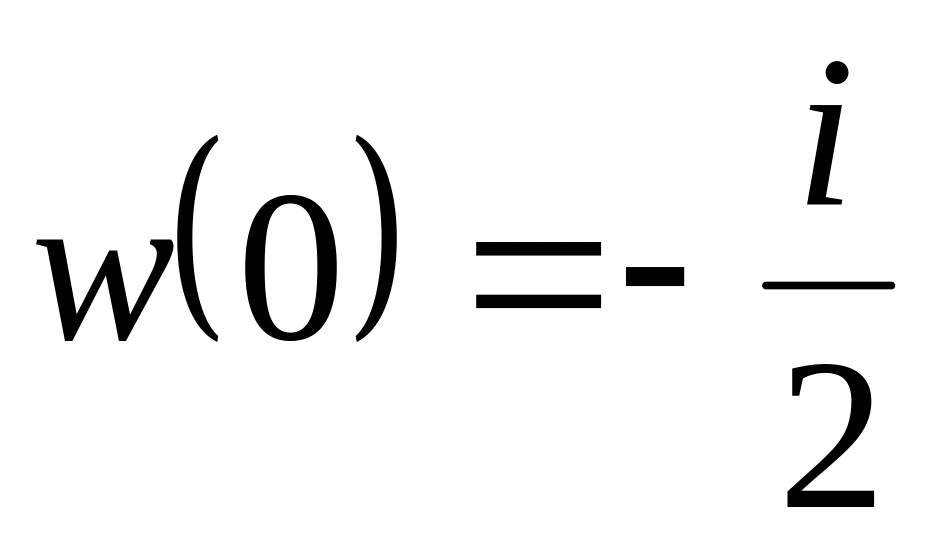 .
.Знайти образ області
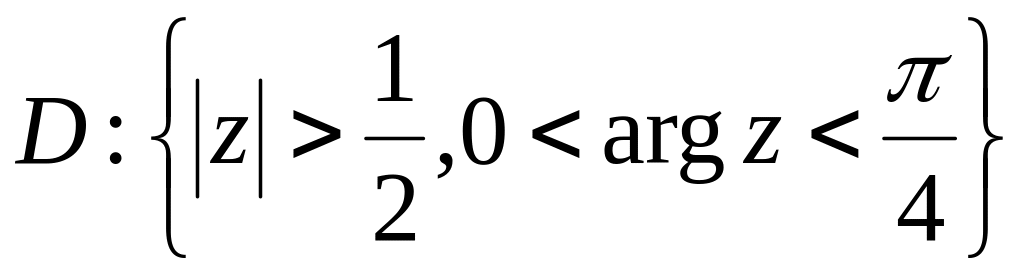 ,
якщо
,
якщо
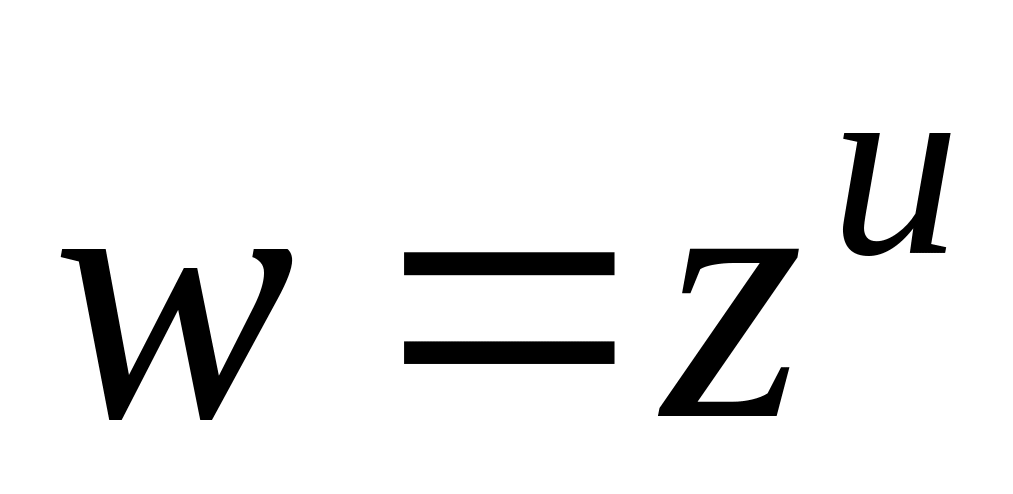 .
.Знайти образ області
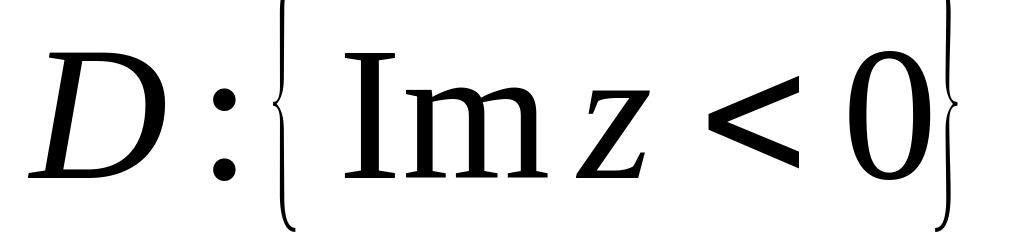 ,
якщо
– багатозначна функція і
,
якщо
– багатозначна функція і
 .
.Обчислити:
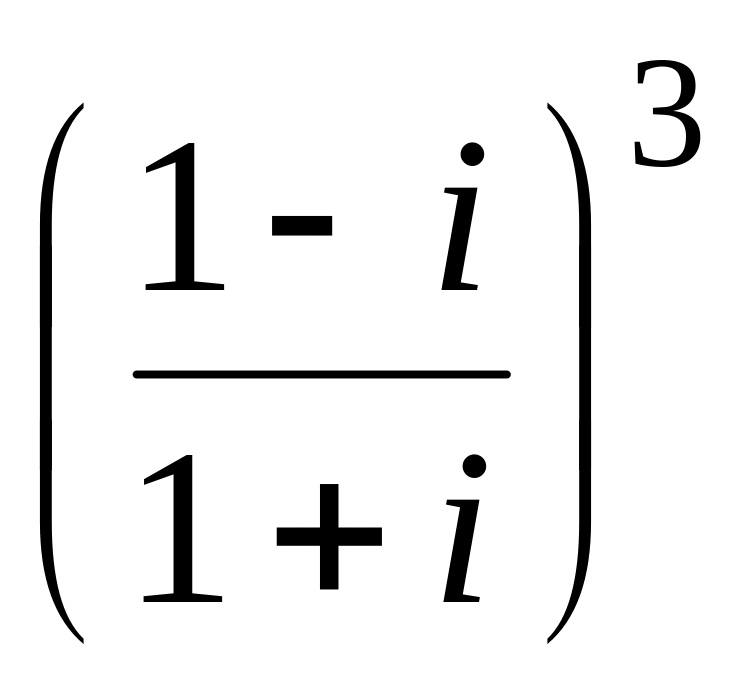 ;
;
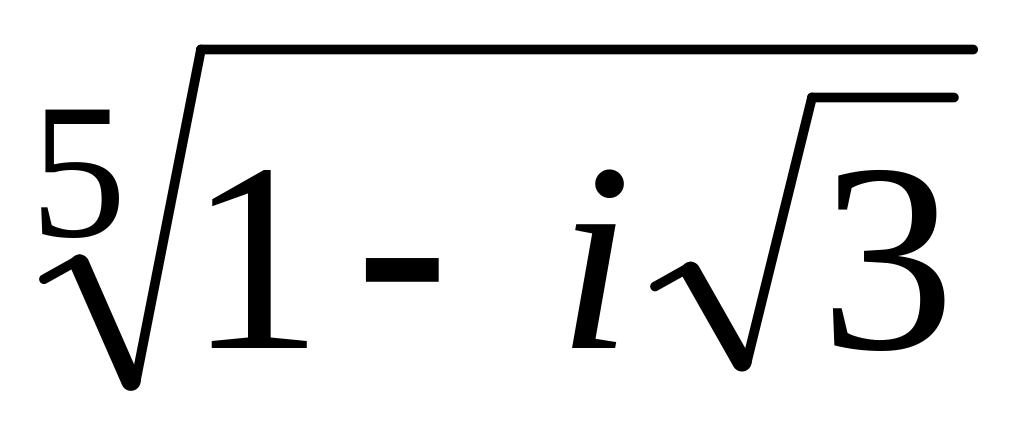 ;
;
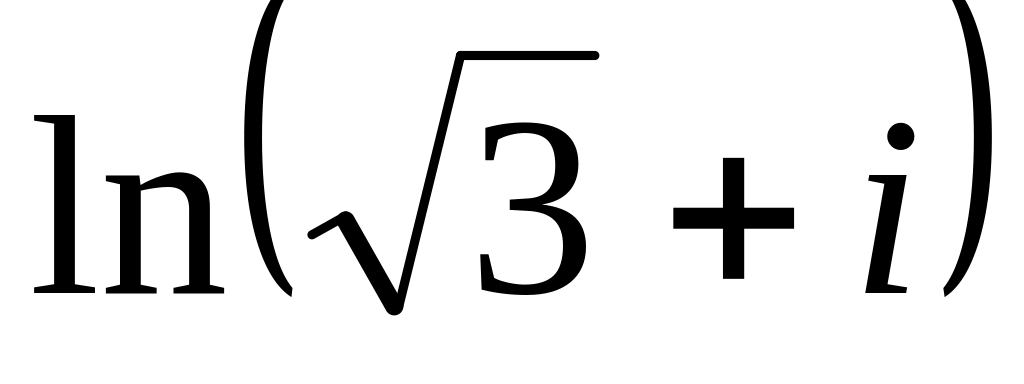 .
.Чи є аналітичною функція ?
Варіант 7
При якому значенні
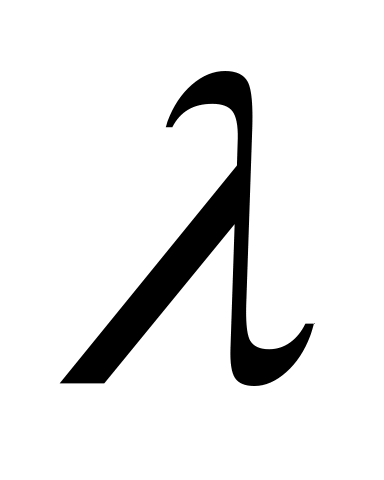 функція
функція
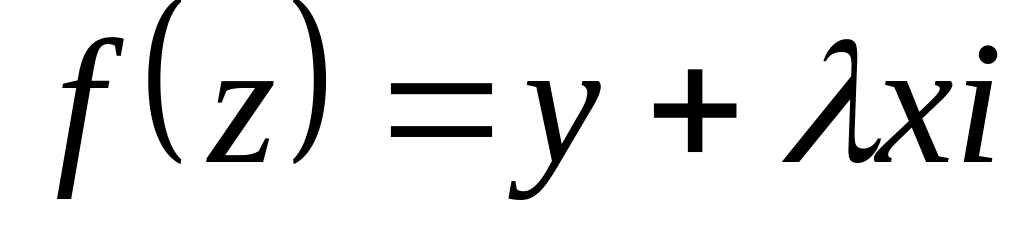 диференційована на всій комплексній
площині.
диференційована на всій комплексній
площині.Знайти дробово-лінійну функцію і образ прямої
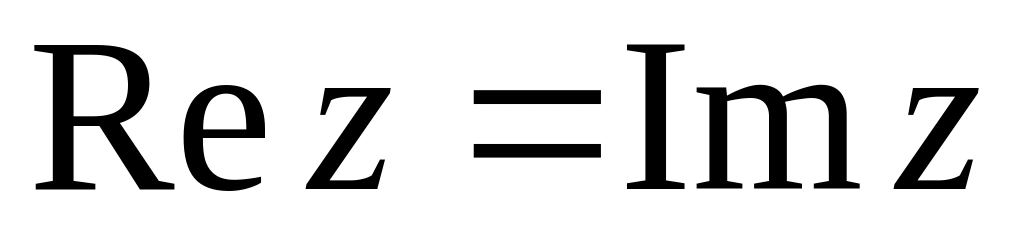 ,
якщо
,
якщо
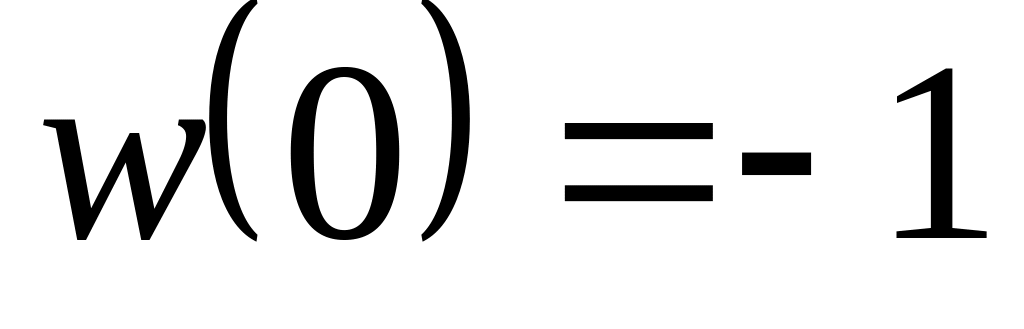 ,
,
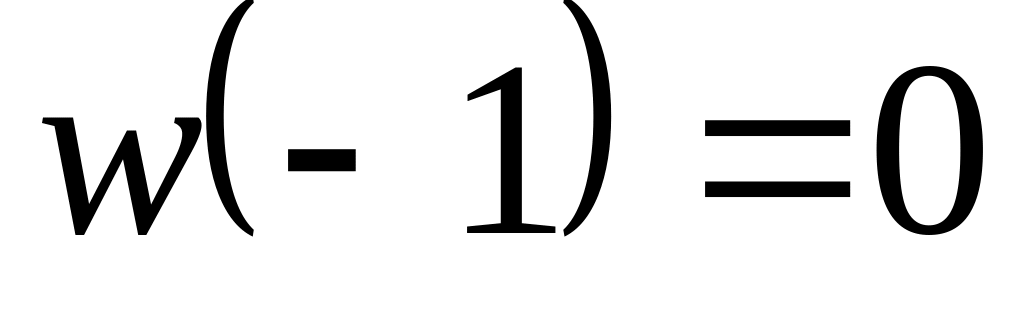 ,
,
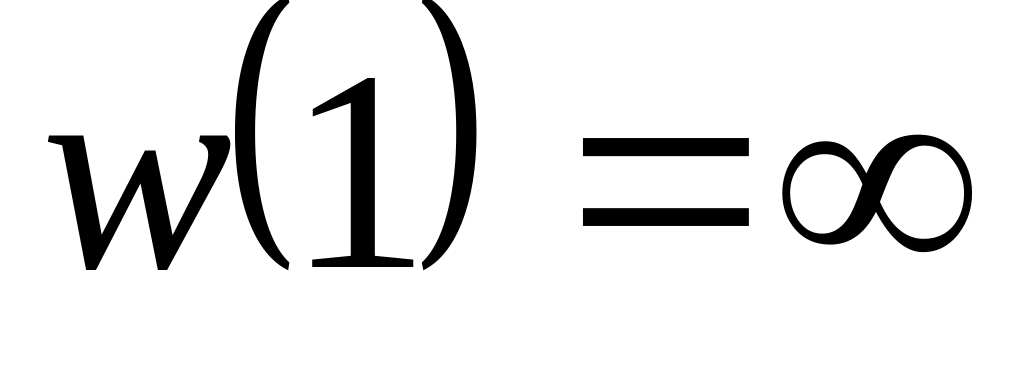 .
.Знайти образ області
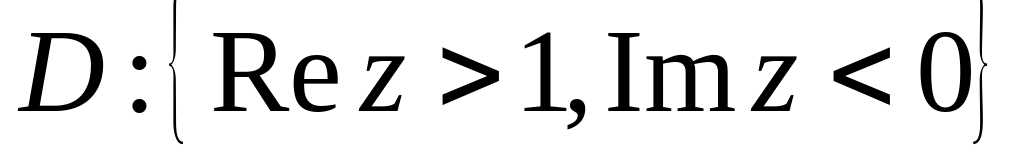 ,
якщо
.
,
якщо
.– багатозначна функція. Знайти образ області
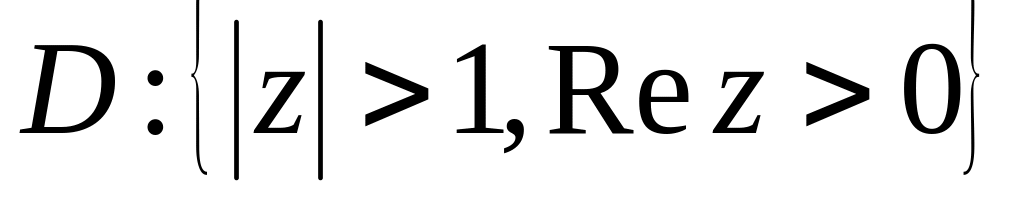 ,
якщо
,
якщо
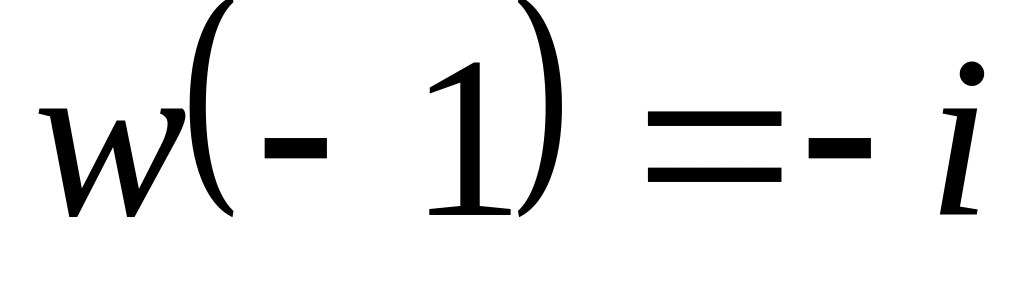 .
.Обчислити
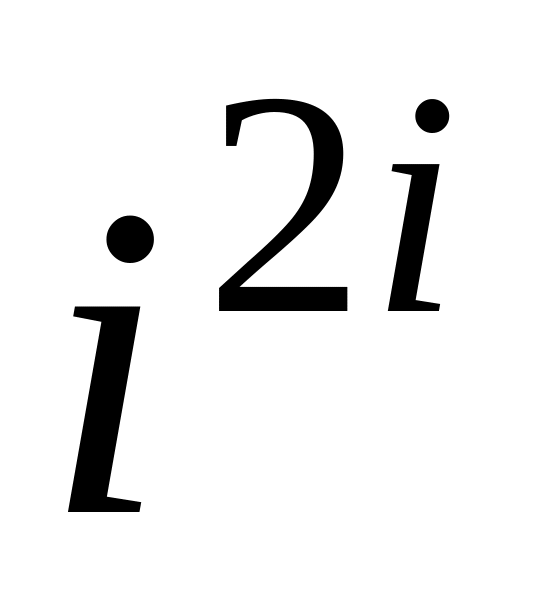 ;
;
;
;
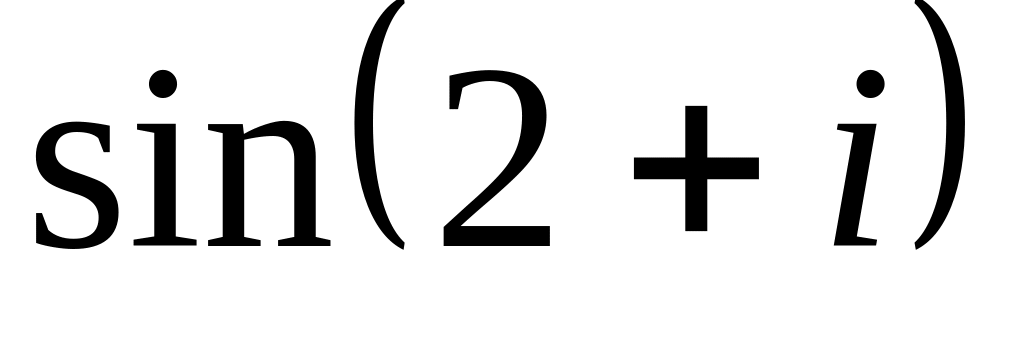 .
.
Чи є функція
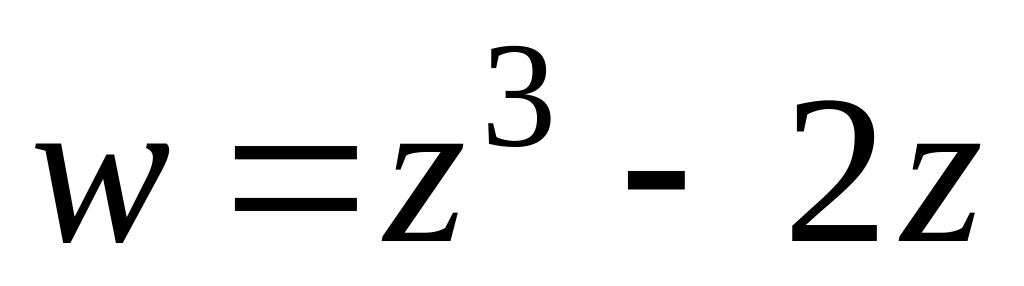 аналітичною?
аналітичною?
Варіант 8
Нехай – аналітична функція
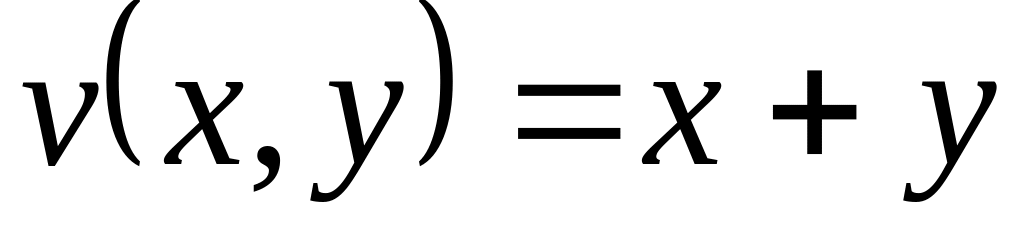 .
Знайти
.
.
Знайти
.Нехай – багатозначна функція. Знайти образ області
 ,
якщо
.
,
якщо
.Нехай . Знайти образи областей
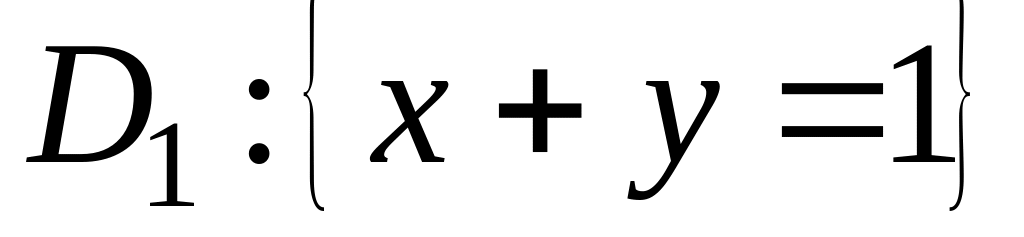 і
і
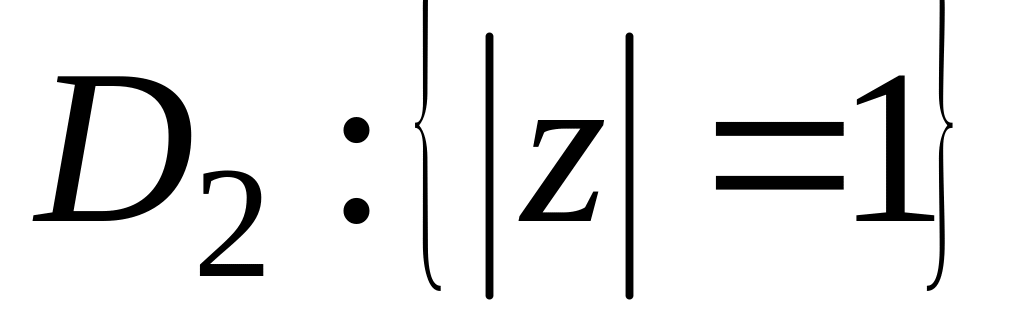 .
.Знайти образ області
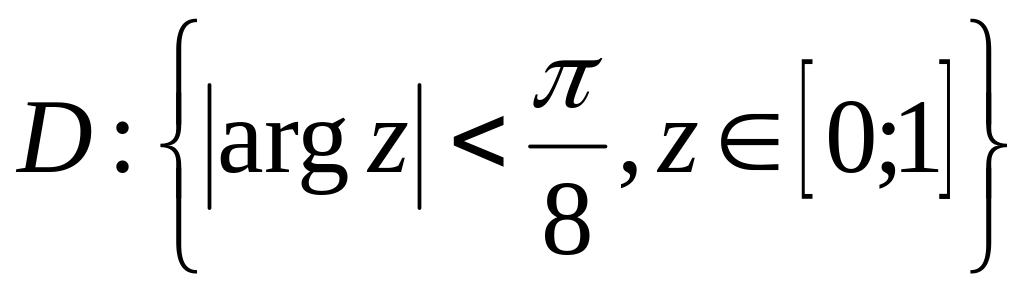 .
.Обчислити: ; ; .
Чи є функція аналітичною?
Варіант 9
При якому значенні функція
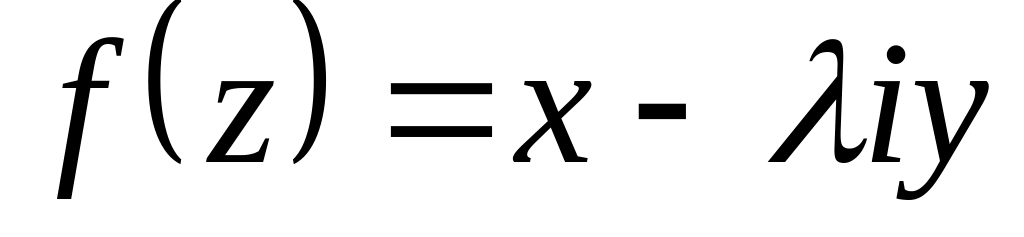 диференційована на всій комплексній
площині.
диференційована на всій комплексній
площині.Знайти дробово-лінійну функцію і образ круга
 ,
якщо
,
,
якщо
,
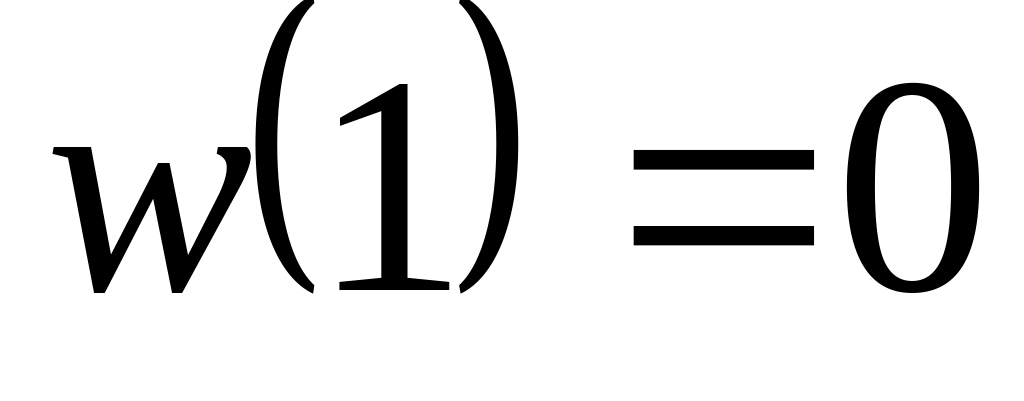 ,
,
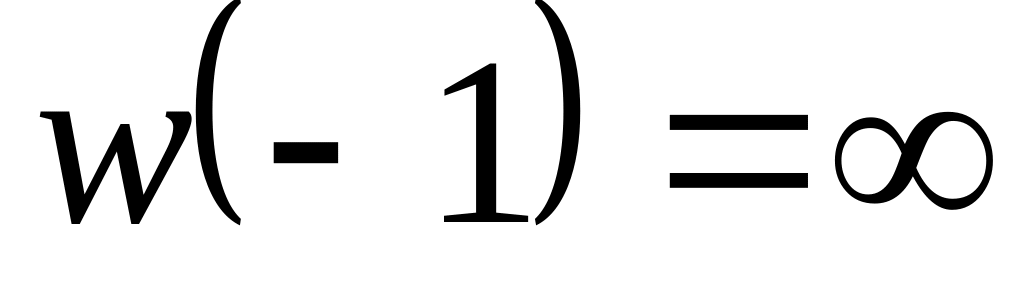 .
.Знайти образ області при відображенні , якщо
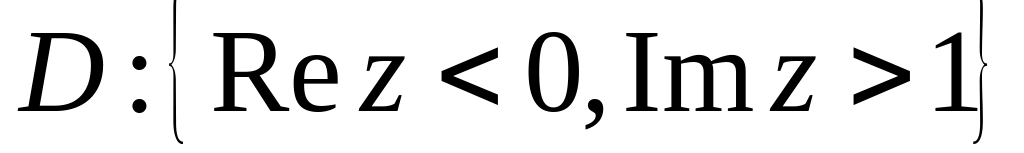 .
.Нехай – багатозначна функція. Знайти образ області
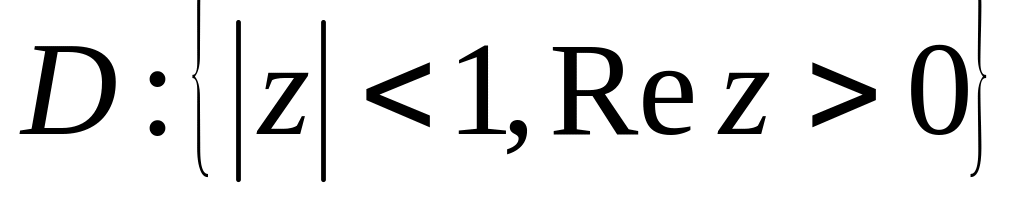 ,
якщо
.
,
якщо
.Обчислити:
 ;
;
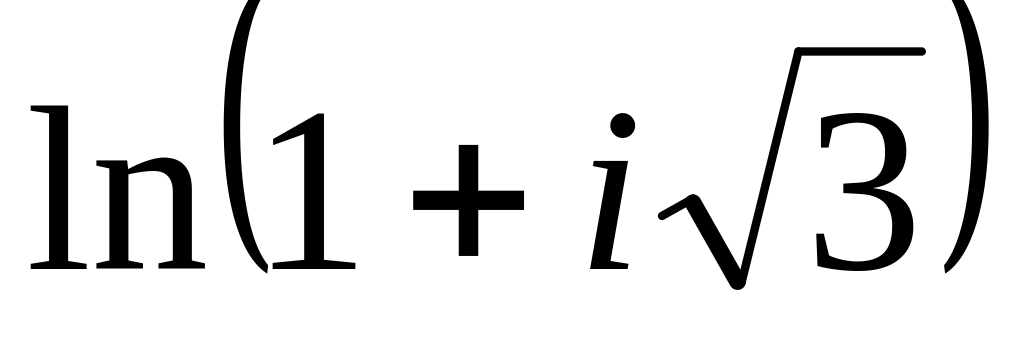 ;
;
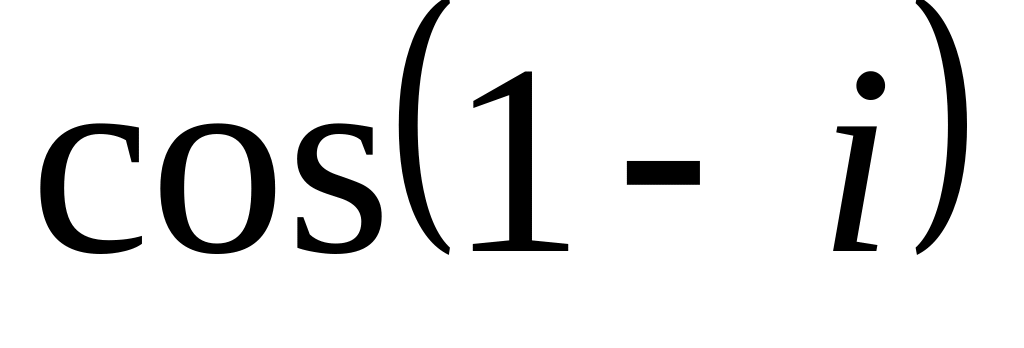 .
.Чи є функція
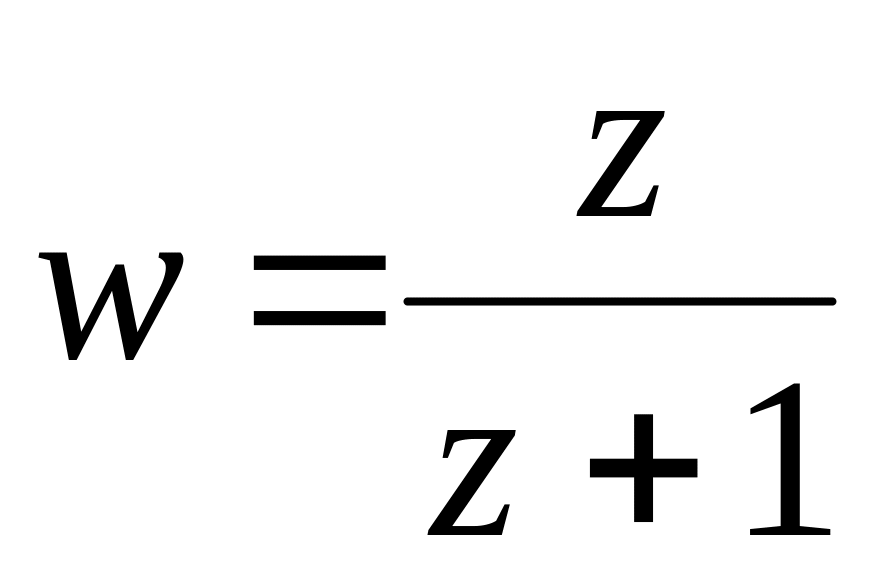 аналітичною?
аналітичною?
Варіант 10
Нехай – аналітична функція. Знайти її, якщо і .
Знайти дробово-лінійну функцію і образ області , якщо
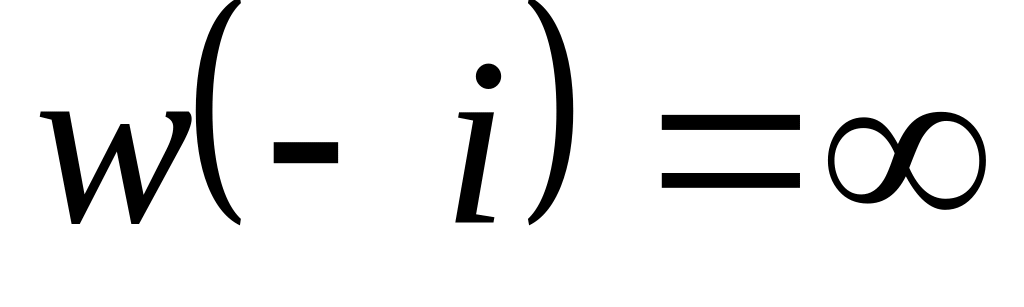 ,
,
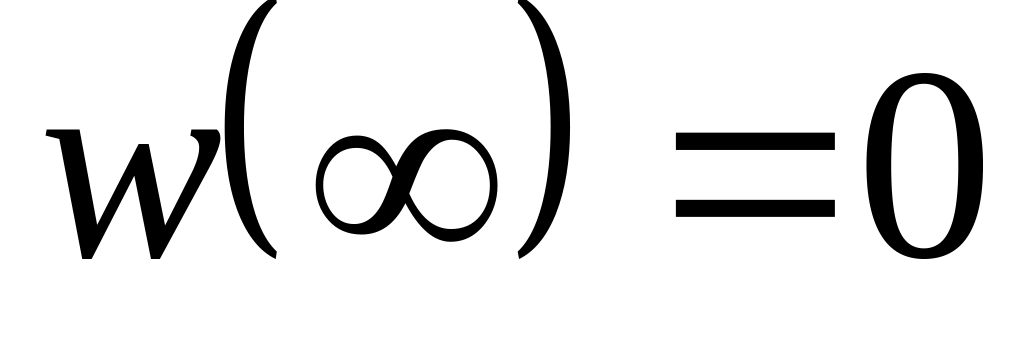 ,
.
,
.Знайти образ області при відображенні , якщо .
Знайти образ області при відображенні віткою багатозначної функції , якщо , .
Обчислити: ;
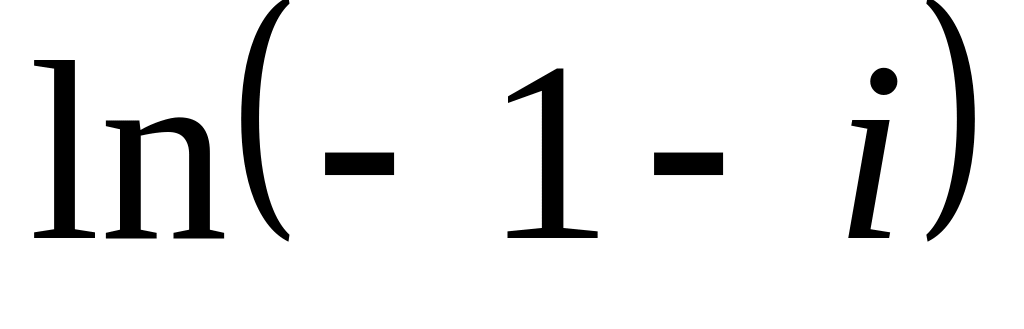 ;
;
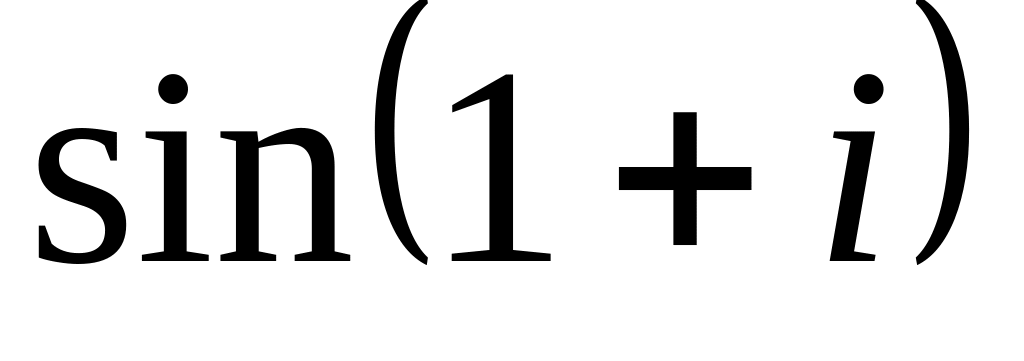 .
.Чи є аналітичною функція ?
Варіант 11
Де функція
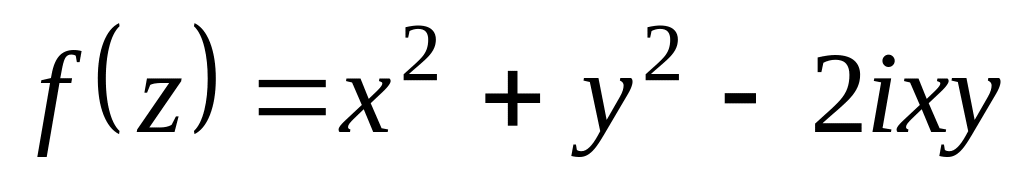 диференційована. Знайти
(там, де вона існує).
диференційована. Знайти
(там, де вона існує).Нехай
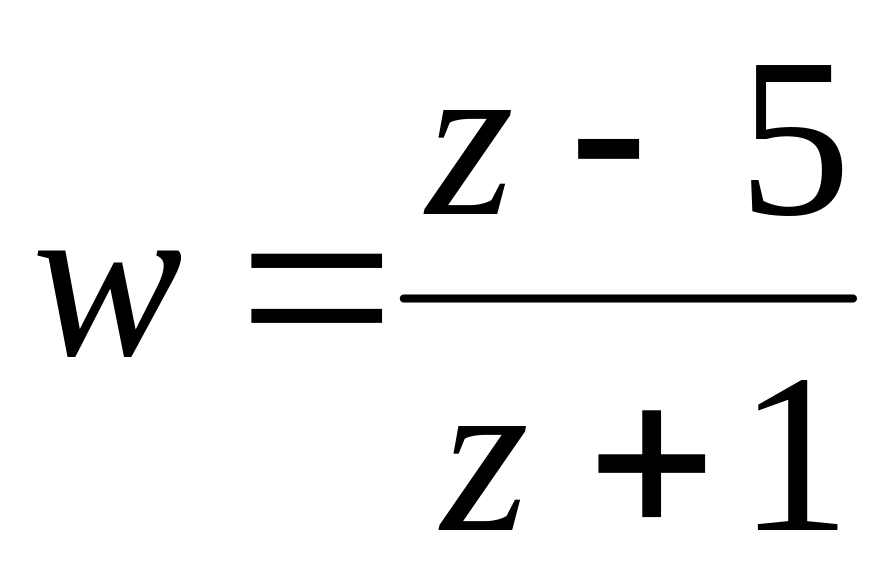 .
Знайти образи областей:
.
Знайти образи областей:
 і
і
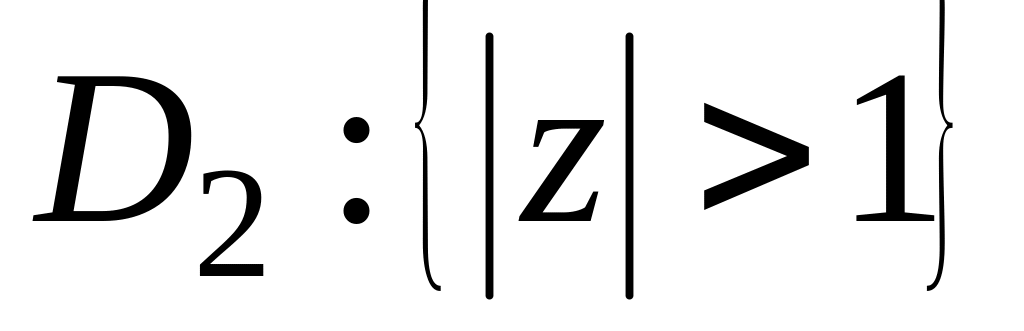 .
.Знайти образ області
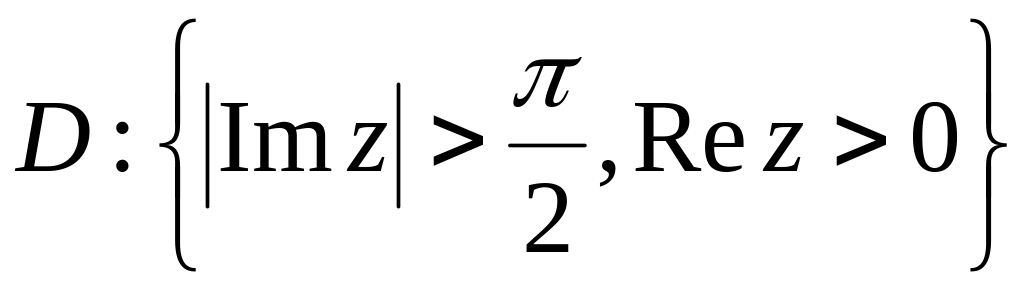 ,
якщо
,
якщо
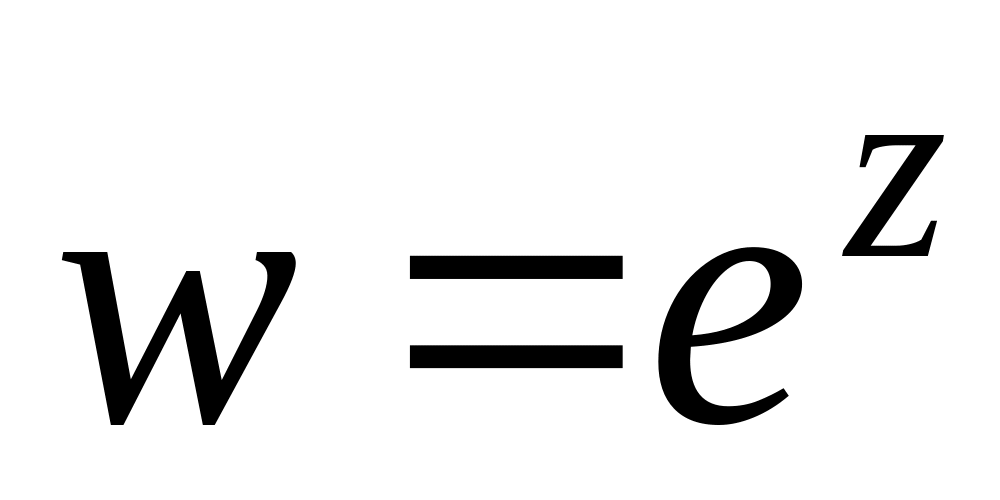 .
.Знайти образ області
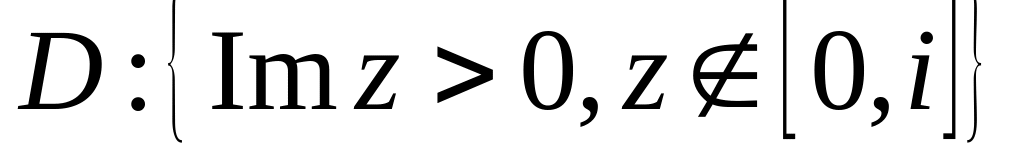 ,
якщо
– багатозначна функція і
.
,
якщо
– багатозначна функція і
.Обчислити: ; ; .
Чи є функція аналітичною?
Варіант 12
Нехай – аналітична функція. Знайти її, якщо
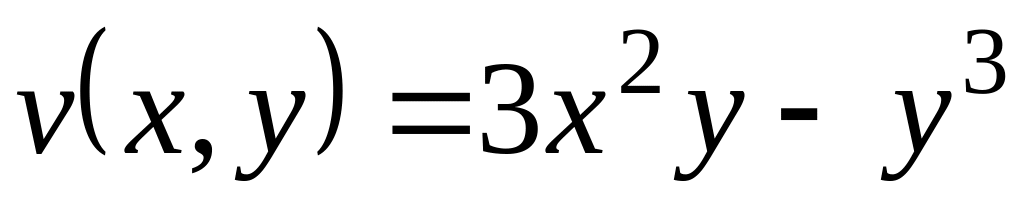 і
і
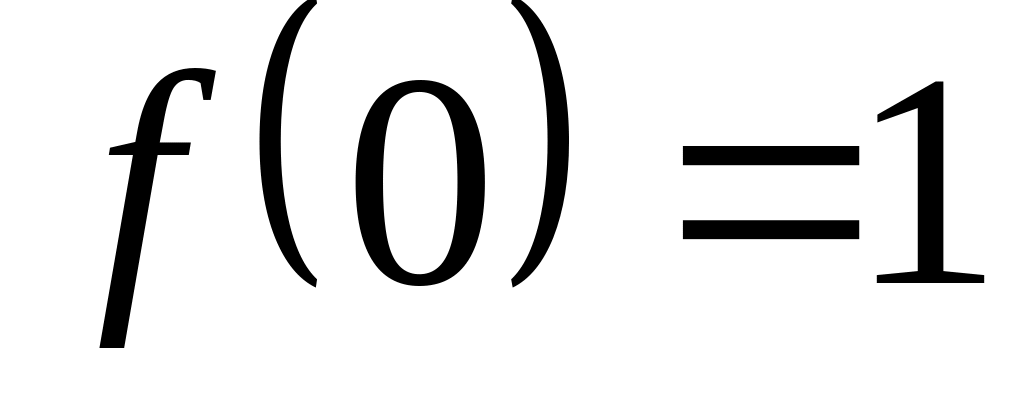 .
.Нехай
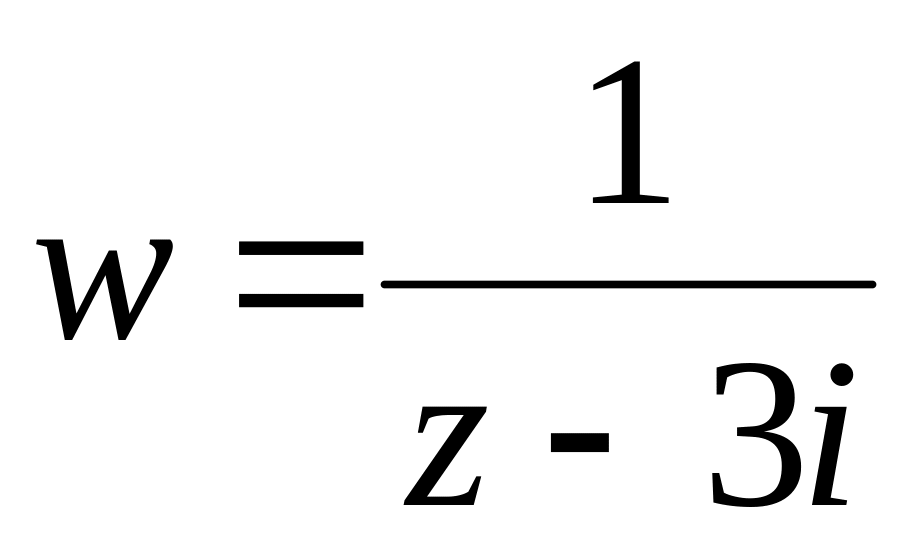 .
Знайти образи областей
.
Знайти образи областей
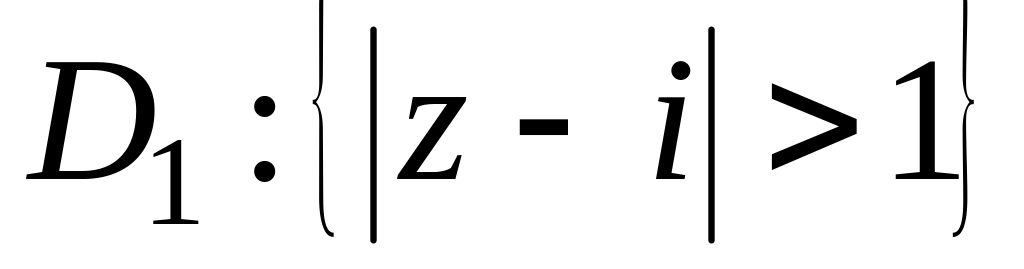 і
і
 .
.Нехай
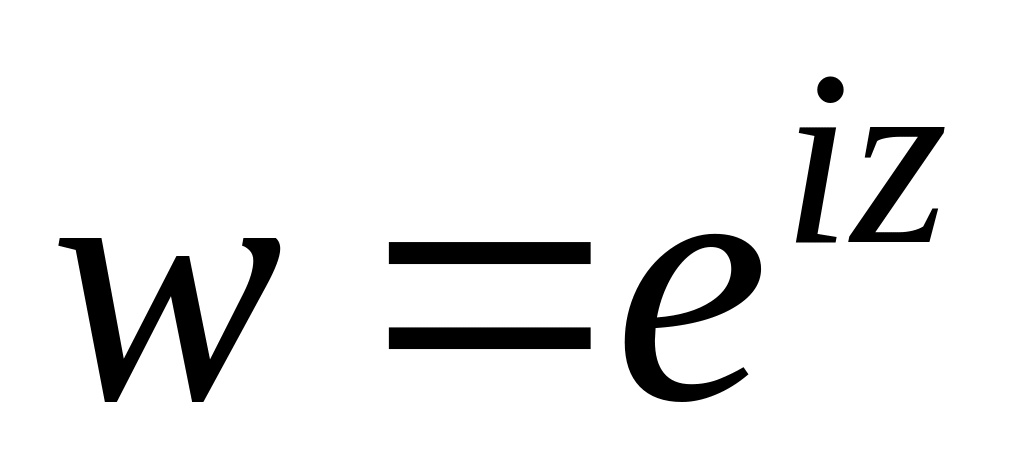 .
Знайти образ області:
.
Знайти образ області:
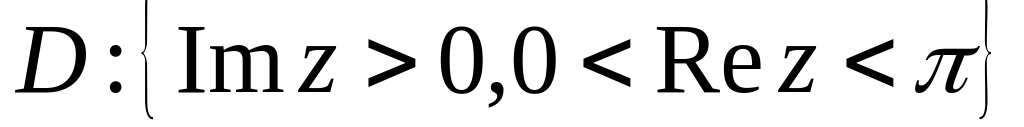 .
.Нехай – багатозначна функція. Знайти образ області
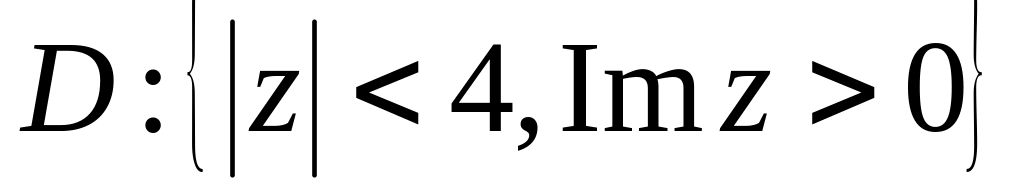 ,
якщо
,
якщо
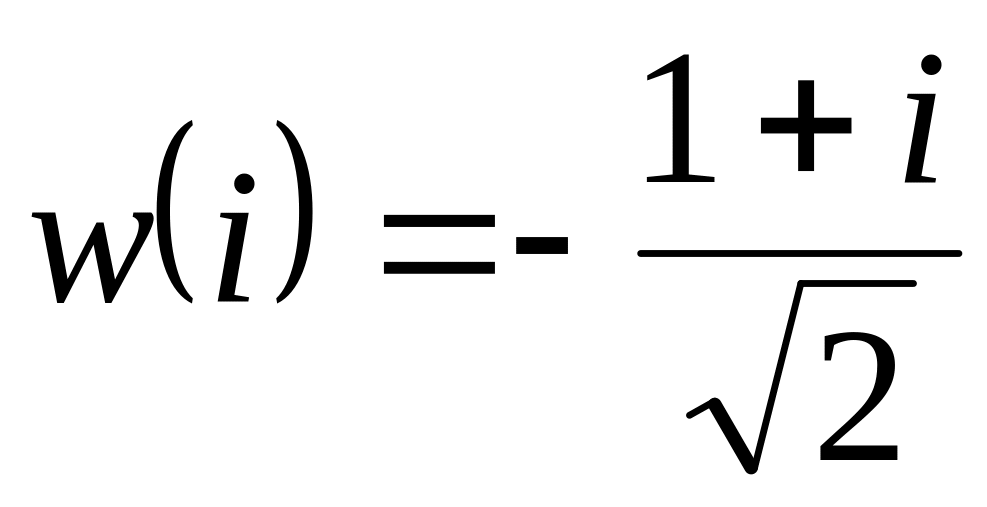 .
.Обчислити: ; ; .
Чи є функція аналітичною?
Варіант 13
Нехай – аналітична функція. Знайти її, якщо
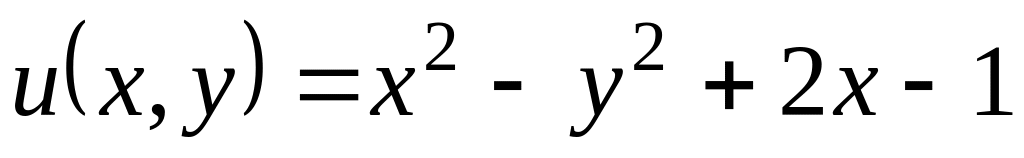 .
.Знайти дробово-лінійну функцію і образ прямої
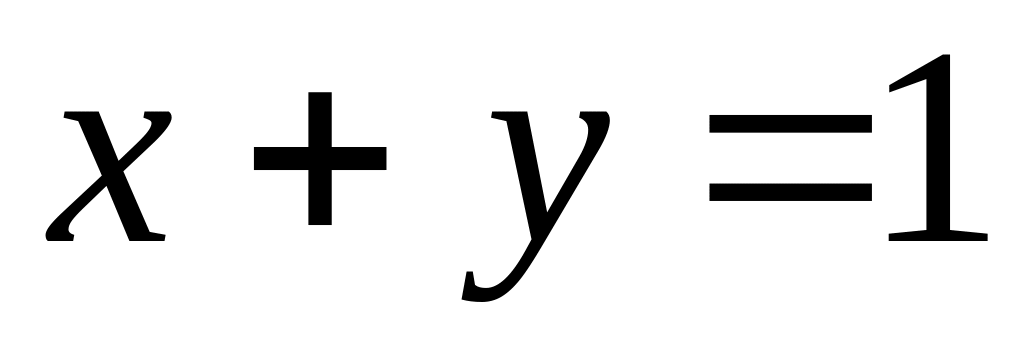 ,
якщо
,
якщо
 ,
,
,
,
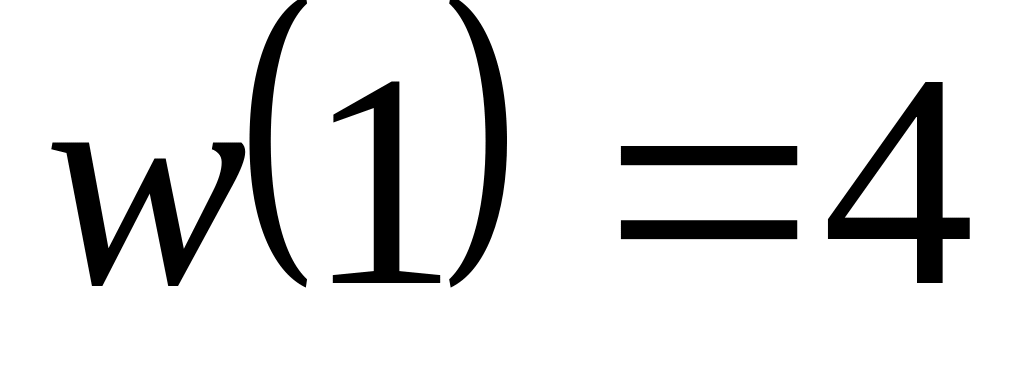 .
.Нехай . Знайти образ області: .
Знайти образ області
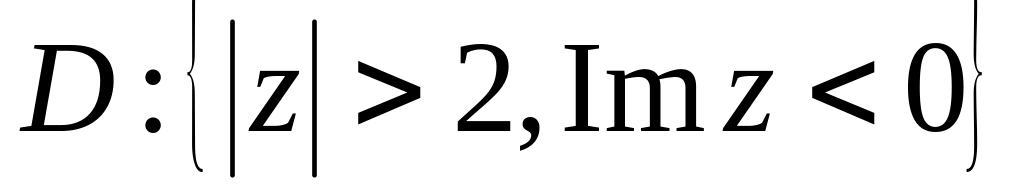 ,
якщо
– багатозначна функція і
.
,
якщо
– багатозначна функція і
.Обчислити ; ; .
Чи є функція аналітичною?
Варіант 14
Нехай – аналітична функція. Знайти її, якщо
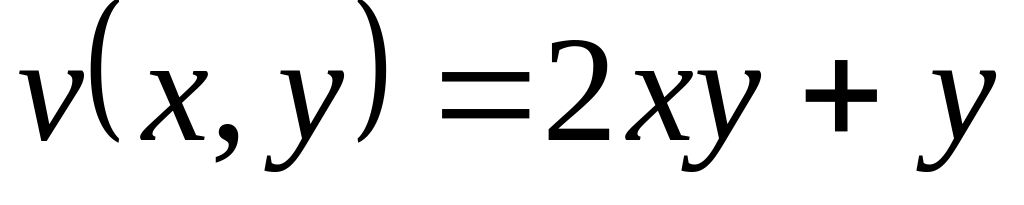 і
і
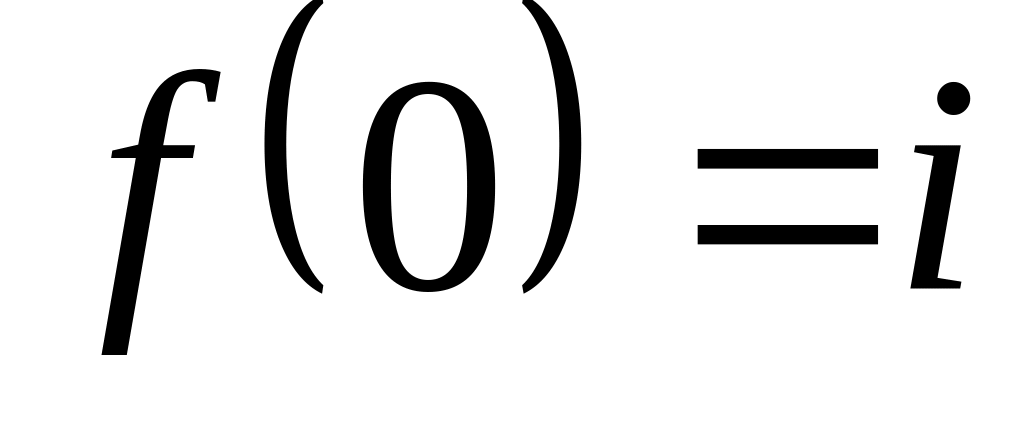 .
.Знайти дробово-лінійну функцію і образ кола
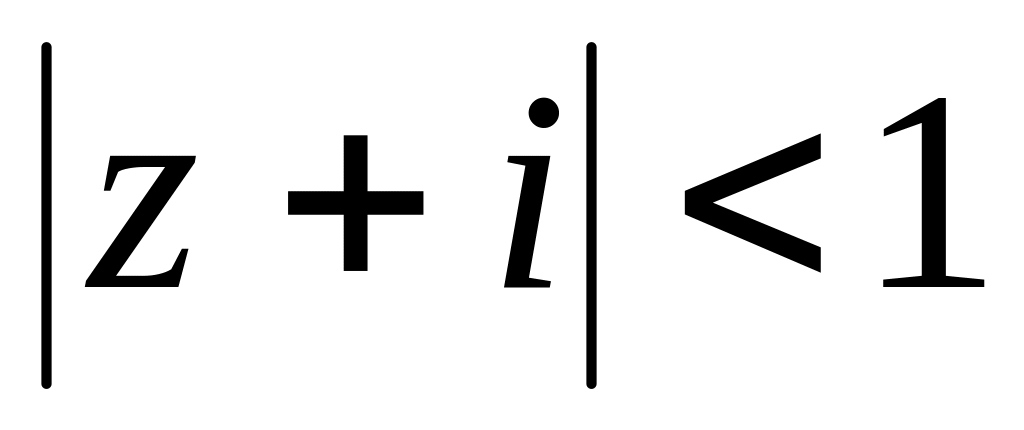 ,
якщо
,
якщо
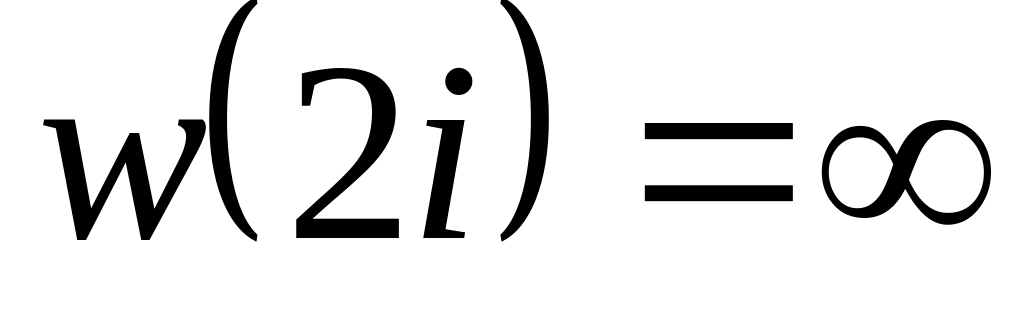 ,
,
 ,
.
,
.Знайти образ області при відображенні , якщо
 .
.Знайти образ області при відображенні регулярною віткою багатозначної функції , якщо
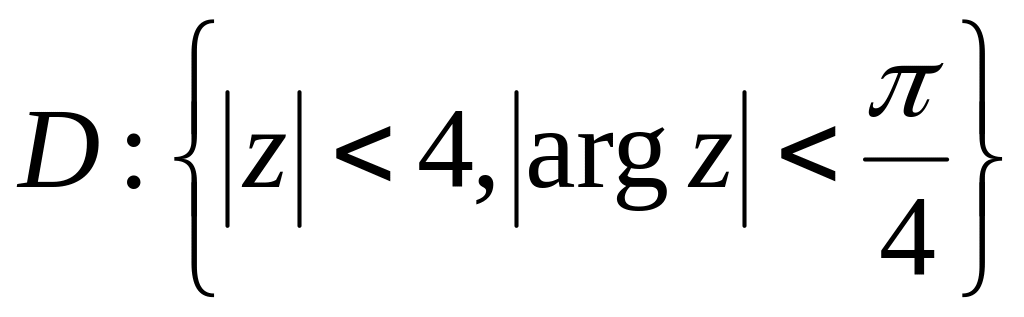 ,
.
,
.Обчислити: ; ; .
Чи є функція
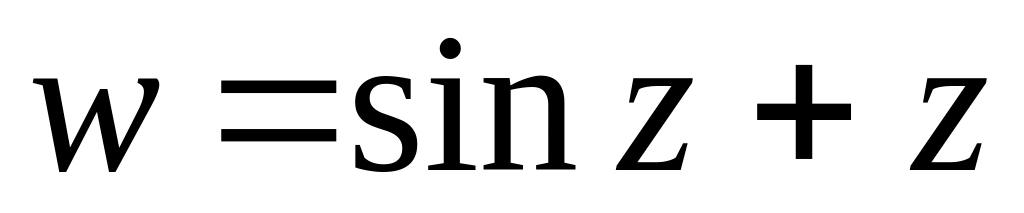 аналітичною?
аналітичною?
Варіант 15
Вияснити, де функція
 диференційована.
диференційована.Знайти дробово-лінійну функцію і образ круга
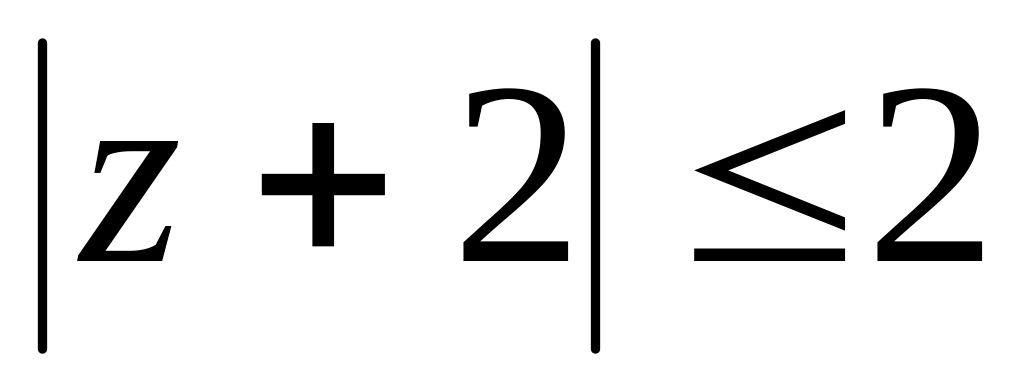 ,
якщо
,
якщо
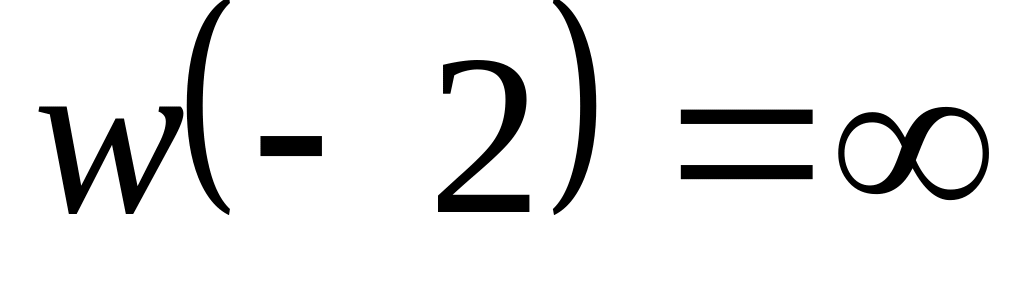 ,
,
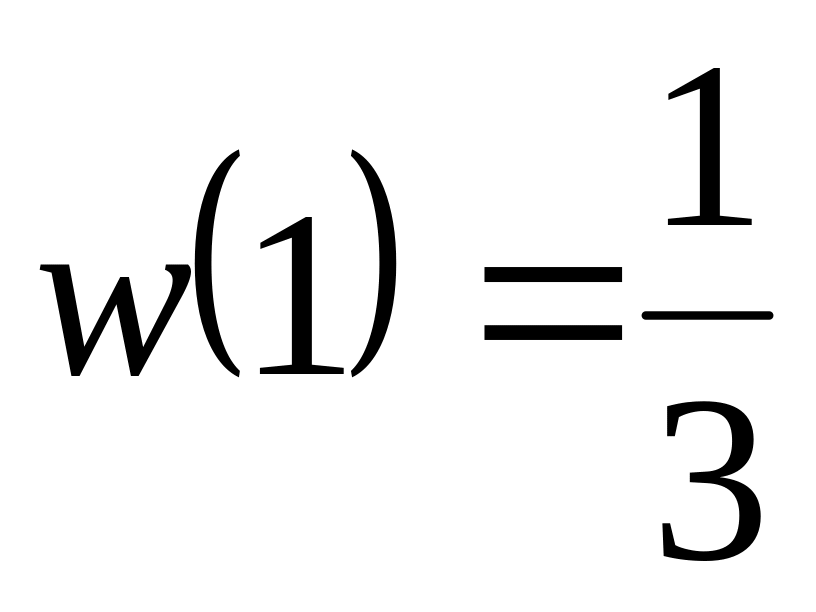 ,
,
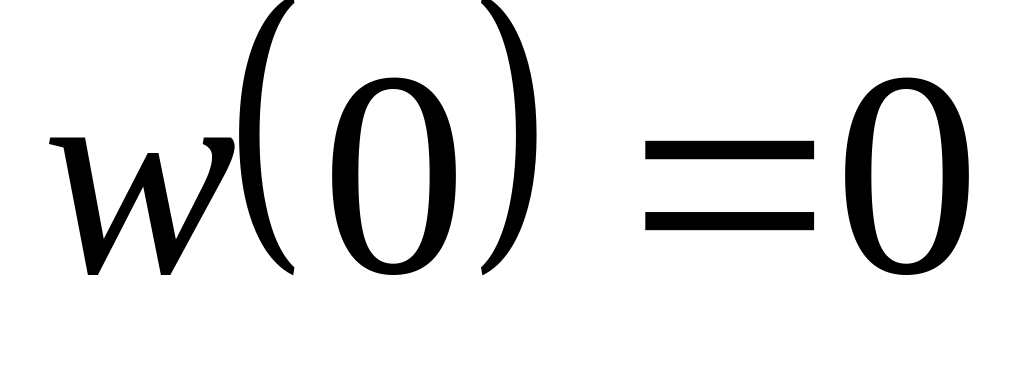 .
.Нехай . Знайти образ області:
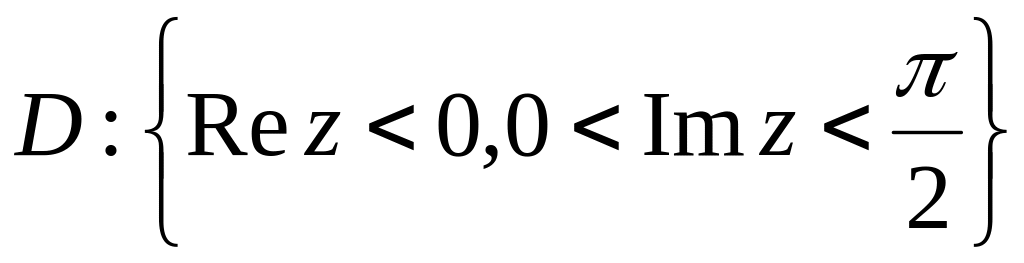 .
.Нехай – багатозначна функція. Знайти образ області
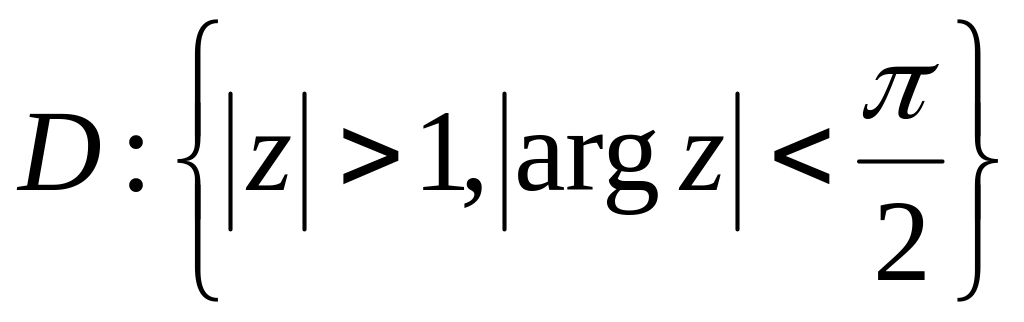 ,
якщо
.
,
якщо
.Обчислити ; ; .
Чи є функція аналітичною?
Варіант 16
При якому

 диференційована на всій комплексній
площині?
диференційована на всій комплексній
площині?
Знайти дробово-лінійну функцію і образ круга
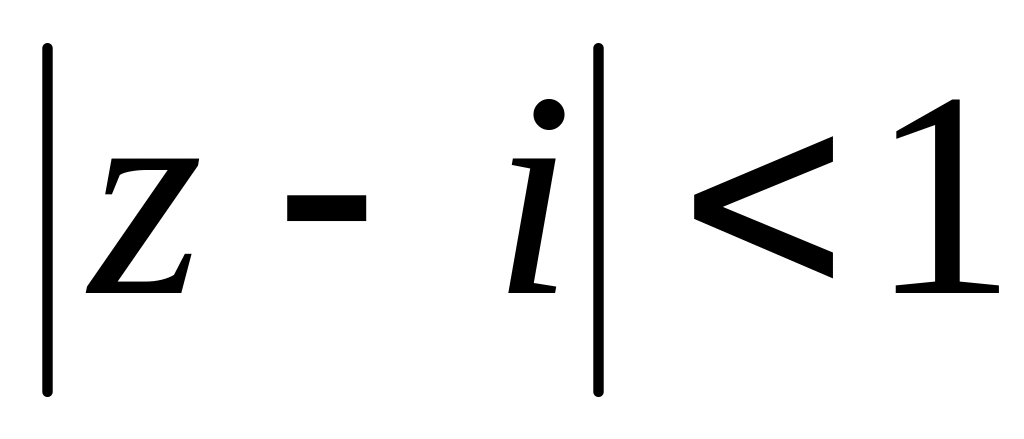 ,
якщо
,
,
якщо
,
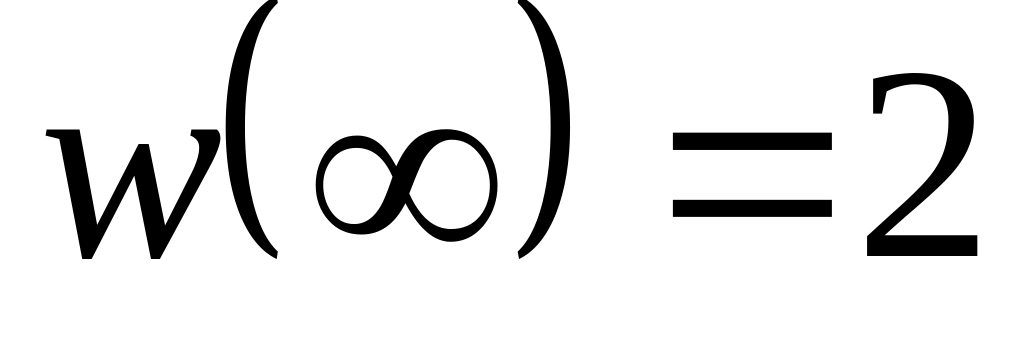 ,
.
,
.Знайти образ області , .
Нехай – багатозначна функція. Знайти образ області , якщо
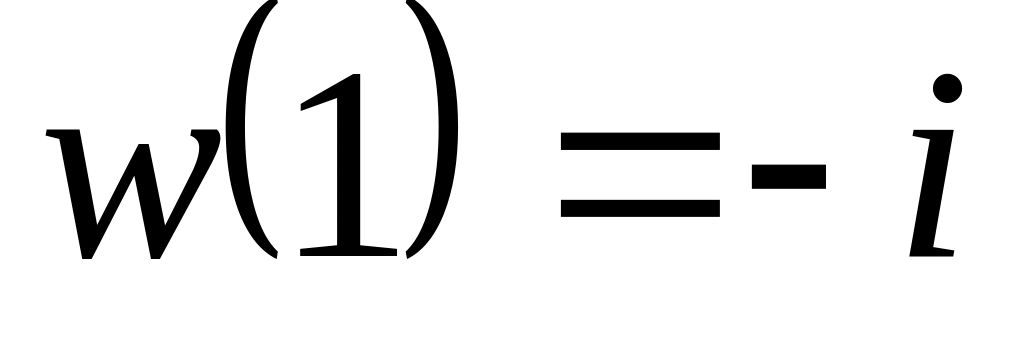 .
.Обчислити: ; ; .
Чи є функція аналітичною?
Варіант 17
При якому
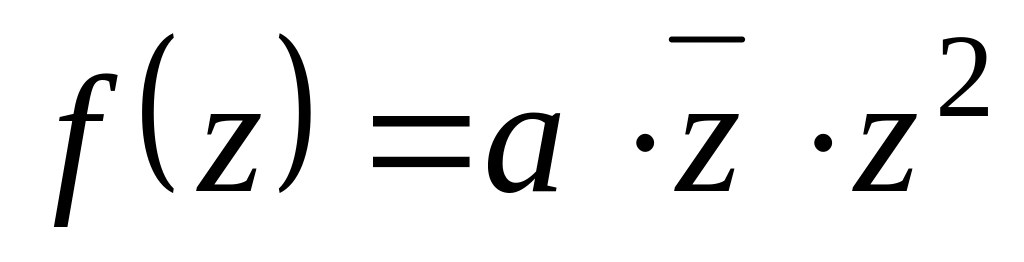 диференційована на всій комплексній
площині?
диференційована на всій комплексній
площині?Знайти дробово-лінійну функцію і образ прямої
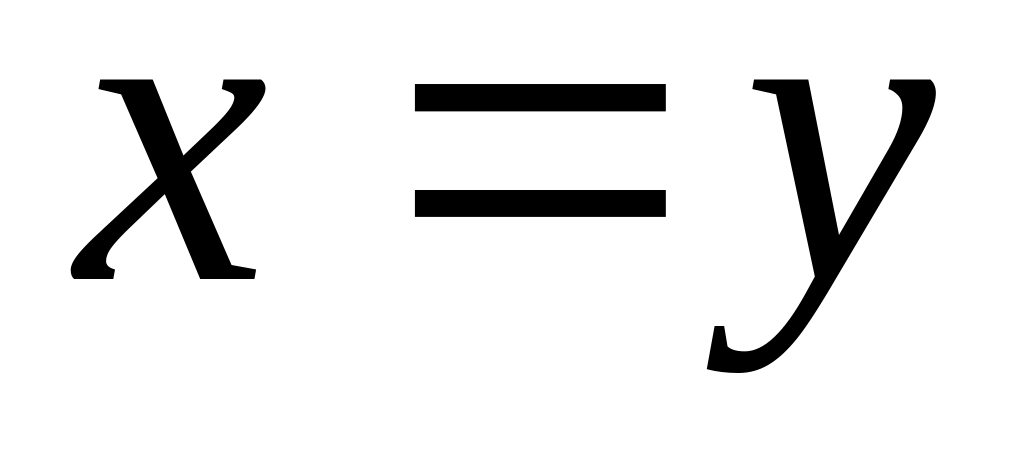 ,
якщо
,
,
,
якщо
,
,
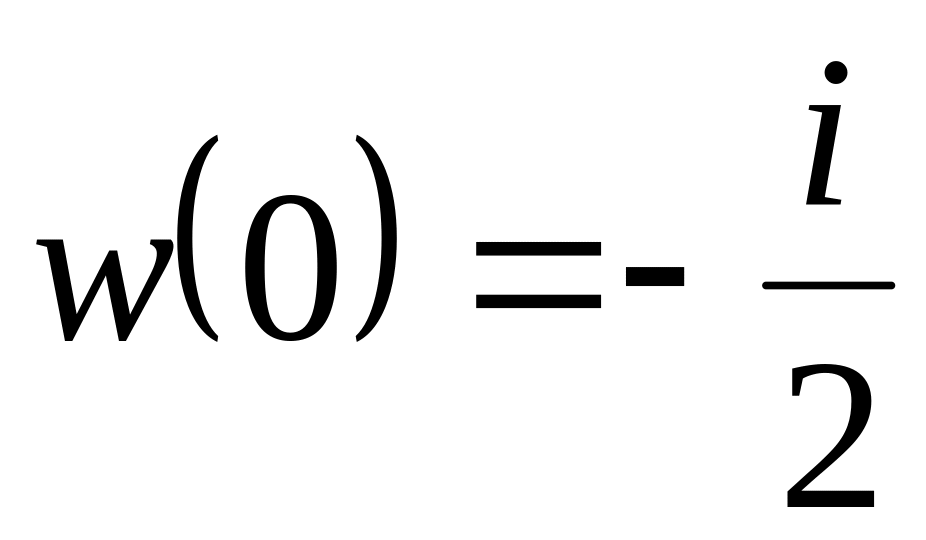 .
.Знайти образ області
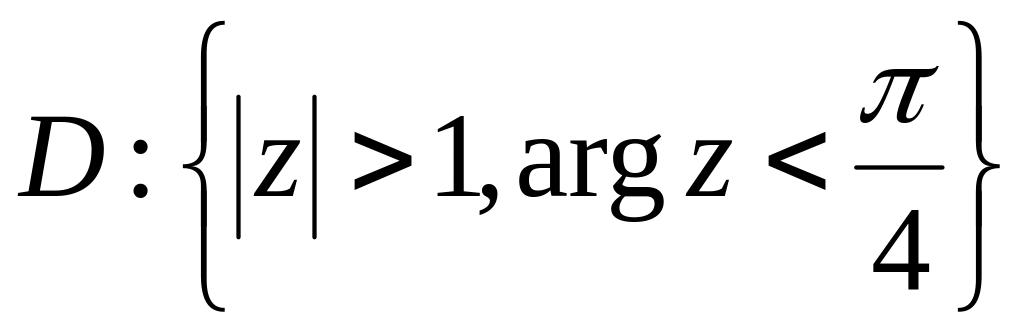 ,
якщо
,
якщо
 .
.Знайти образ області , якщо – багатозначна функція і
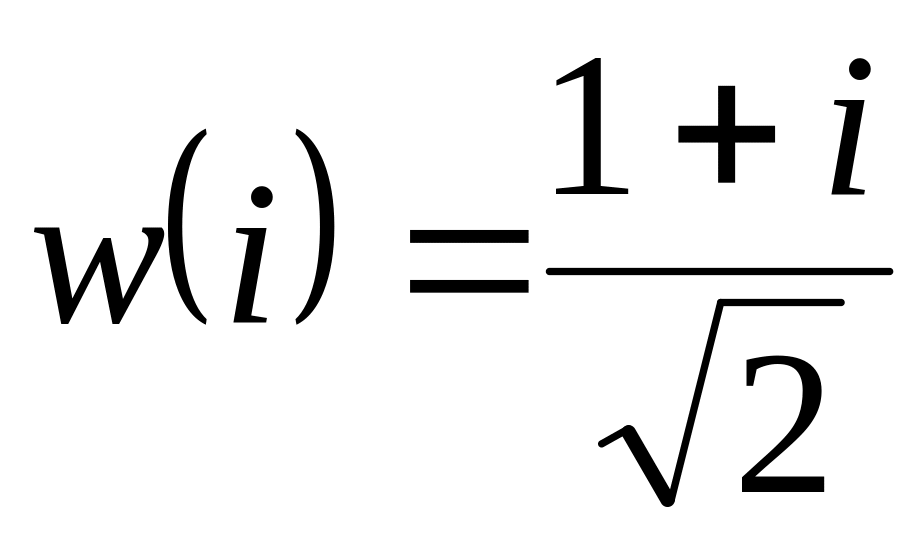 .
.Обчислити:
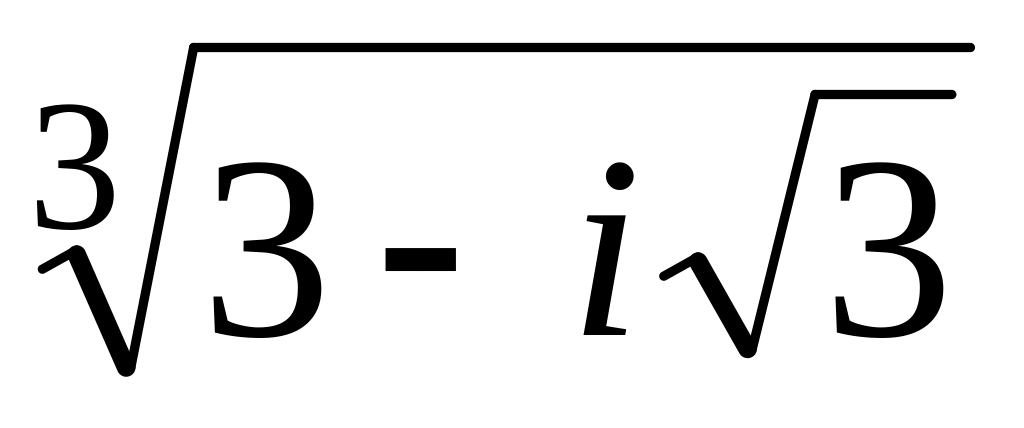 ;
;
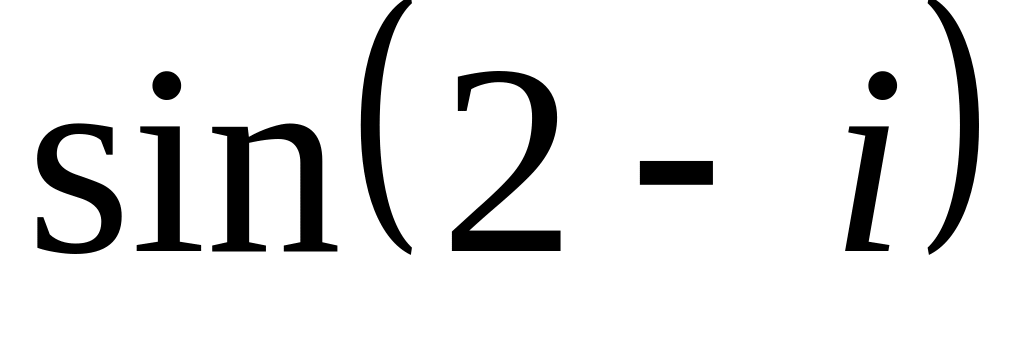 ;
;
 .
.
Чи є функція аналітичною?
Варіант 18
При якому
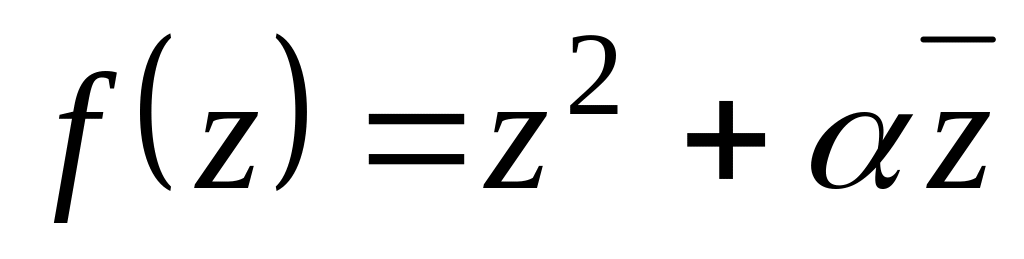 диференційована на всій комплексній
площині?
диференційована на всій комплексній
площині?Знайти дробово-лінійну функцію і образ круга
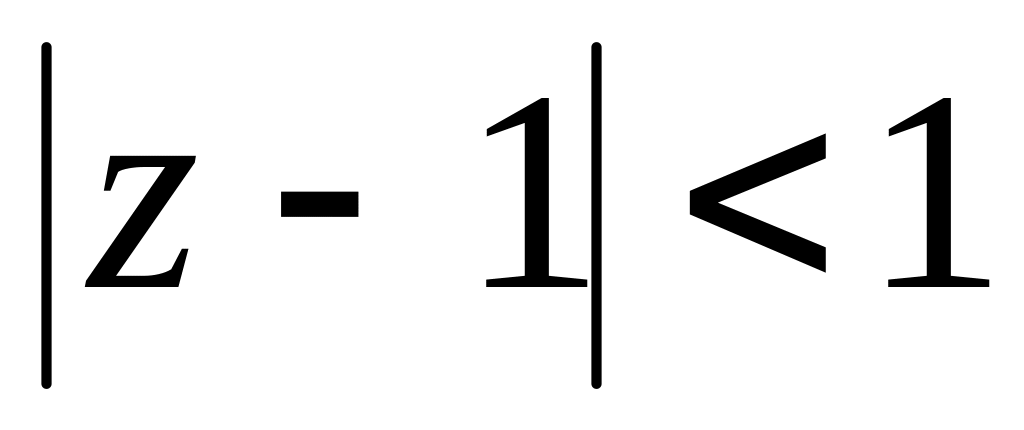 ,
якщо
,
,
.
,
якщо
,
,
.Знайти образ області
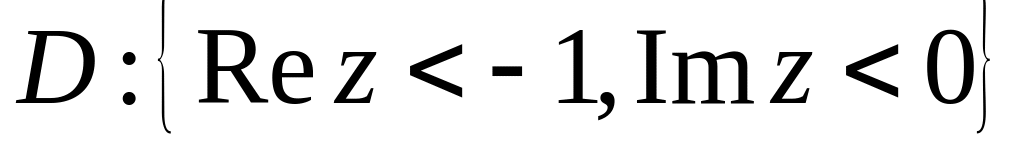 ,
.
,
.Нехай – багатозначна функція. Знайти образ області
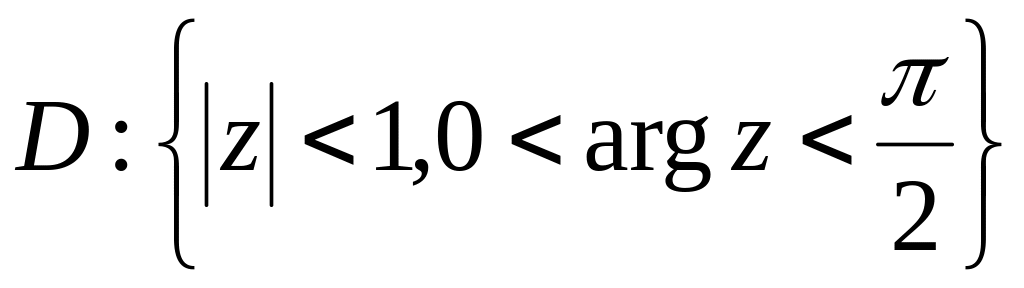 ,
якщо
.
,
якщо
.Обчислити: ; ; .
Чи є функція аналітичною?
Варіант 19
Нехай – аналітична функція. Знайти її, якщо і .
Знайти дробово-лінійну функцію і образ круга , якщо , , .
Знайти образ області
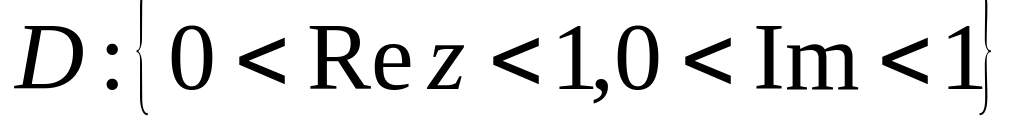 при відображенні
при відображенні
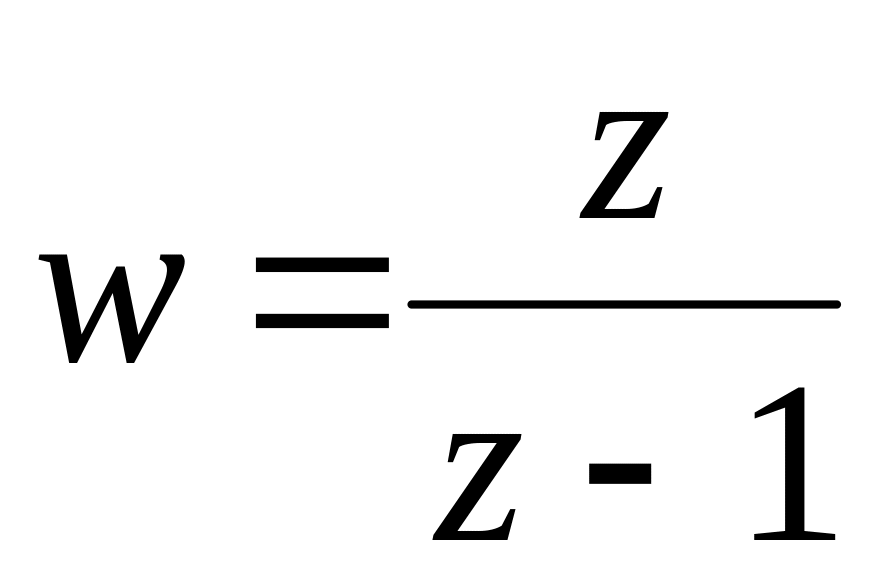 .
.Знайти образ області , якщо – багатозначна функція і .
Обчислити: ; ; .
Чи є функція аналітичною?
Варіант 20
Нехай – аналітична функція. Знайти її, якщо
 .
.Нехай . Знайти образи областей і .
Знайти дробово-лінійну функцію, яка одиничний круг
 відображає на круг
відображає на круг
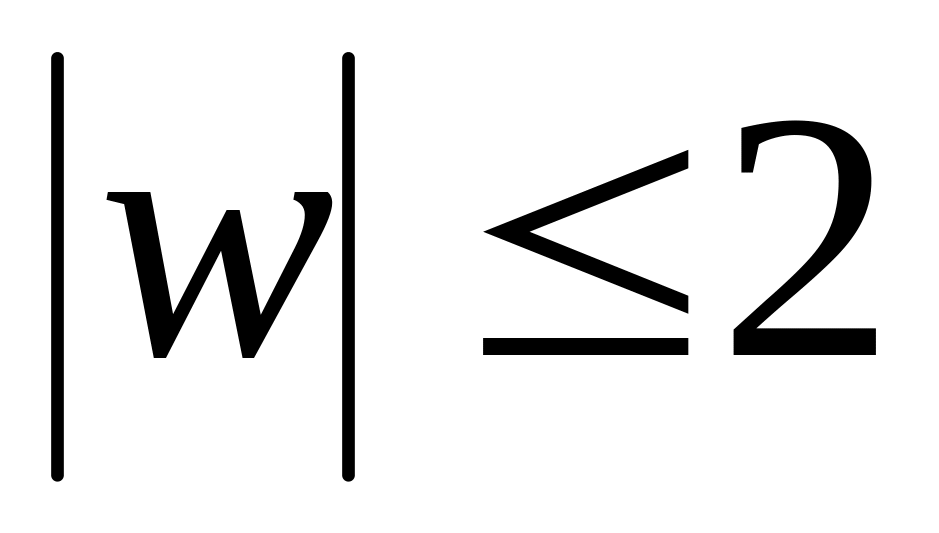 ,
причому так, що точка
,
причому так, що точка
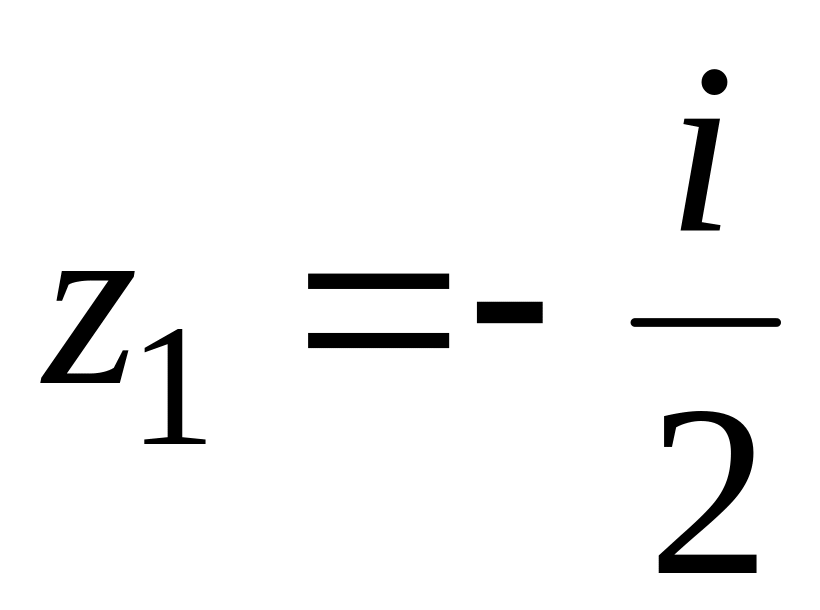 переходить в точку
переходить в точку
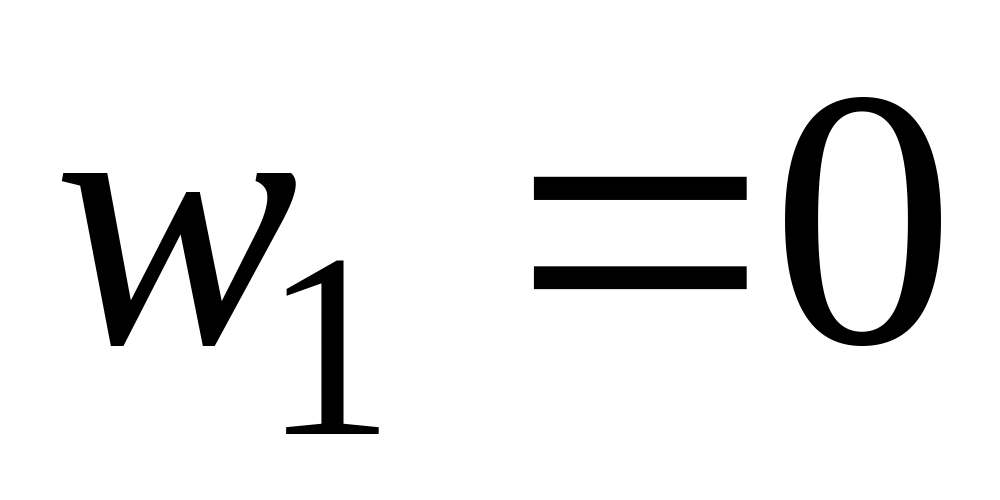 ,
а
,
а
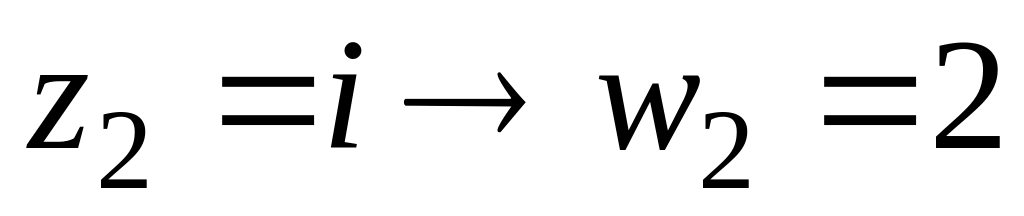 .
.Нехай – багатозначна функція. Знайти образ області , якщо .
Обчислити ; ; .
Чи є аналітичною функція ?
Варіант 21
1. Використовуючи умову Коші-Римана, довести, що диференційована в комплексній площині і знайти , якщо .
2. Нехай , знайти образи областей: і .
3. Нехай . Знайти образ області: .
4. Нехай – багатозначна функція. Знайти образ області , якщо .
5. Обчислити: ; ; .
6. Чи є функція аналітичною?
Варіант 22
1. Нехай – аналітична функція. Знайти її, якщо , .
2. Знайти дробово-лінійну функцію і образ області , якщо , , .
3. Знайти образ області при відображенні , якщо .
4. Знайти образ області при відображенні віткою багатозначної функції , якщо , .
5. Обчислити: ; ; .
6. Чи є функція аналітичною?
Варіант 23
1. Використовуючи умову Коші-Римана, довести, що диференційована в комплексній площині і знайти , якщо .
2. Нехай , знайти образи областей: і .
3. Нехай . Знайти образ області: .
4. Нехай – багатозначна функція. Знайти образ області , якщо .
5. Обчислити: ; ; .
6. Чи є аналітичною функція ?
Варіант 24
1. Нехай – аналітична функція. Знайти її, якщо і .
2. Знайти дробово-лінійну функцію і образ області , якщо , , .
3. Знайти образ області при відображенні , якщо .
4. Знайти образ області при відображенні віткою багатозначної функції , якщо , .
5. Обчислити: ; ; .
6. Чи є функція аналітичною?
Варіант 25
1. Нехай – аналітична функція. Знайти її, якщо .
2. Нехай . Знайти образи областей і .
3. Знайти образ області , якщо .
4. Нехай – багатозначна функція. Знайти образ області , якщо .
5. Обчислити: ; ; .
6. Чи є аналітичною функція ?
Варіант 26
1. При якому значенні диференційована у всій комплексній площині?
2. Знайти дробово-лінійну функцію і образ області , якщо , , .
3. Знайти образ області , якщо .
4. Знайти образ області , якщо – багатозначна функція і .
5. Обчислити: ; ; .
6. Чи є аналітичною функція ?
Варіант 27
1. При якому значенні функція диференційована на всій комплексній площині.
2. Знайти дробово-лінійну функцію і образ прямої , якщо , , .
3. Знайти образ області , якщо .
– багатозначна функція. Знайти образ області , якщо .
4. Обчислити ; ; .
5. Чи є функція аналітичною?
Варіант 28
1. Нехай – аналітична функція . Знайти .
2. Нехай – багатозначна функція. Знайти образ області , якщо .
3. Нехай . Знайти образи областей і .
4. Знайти образ області .
5. Обчислити: ; ; .
6. Чи є функція аналітичною?