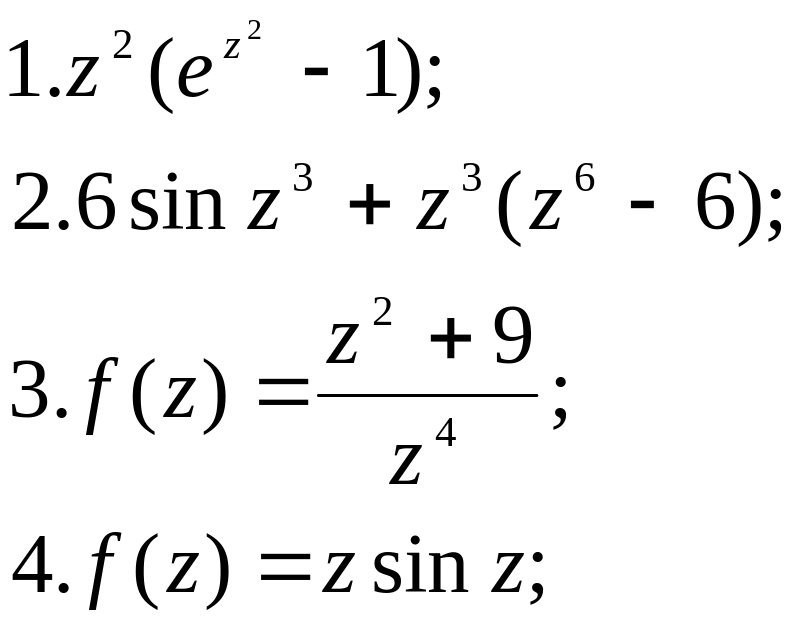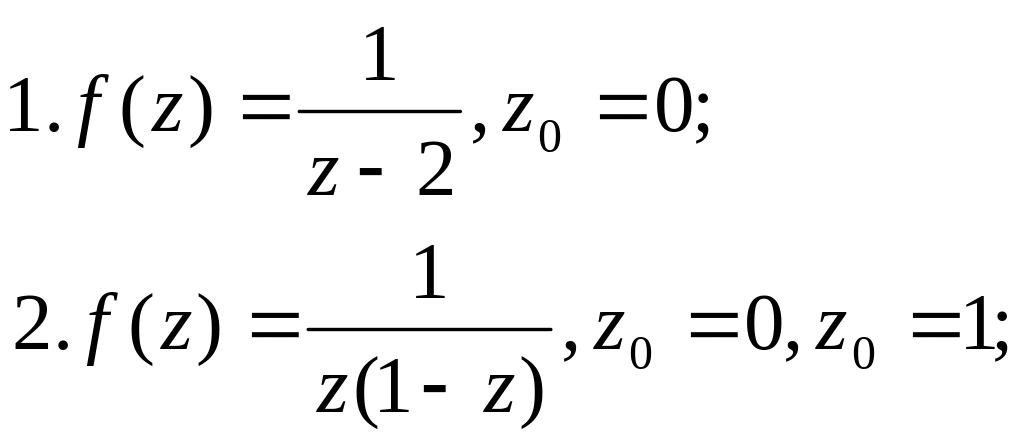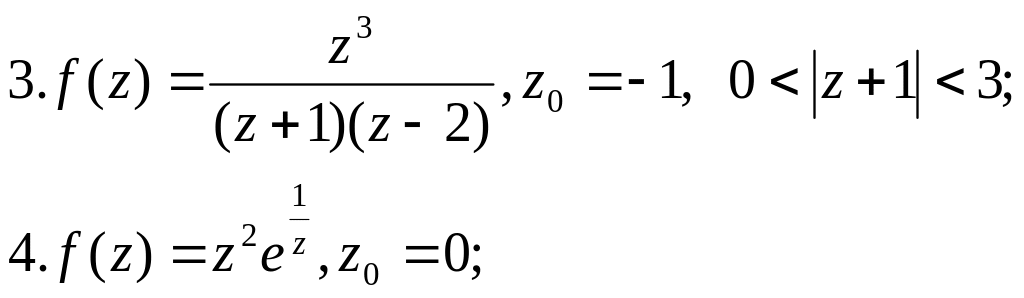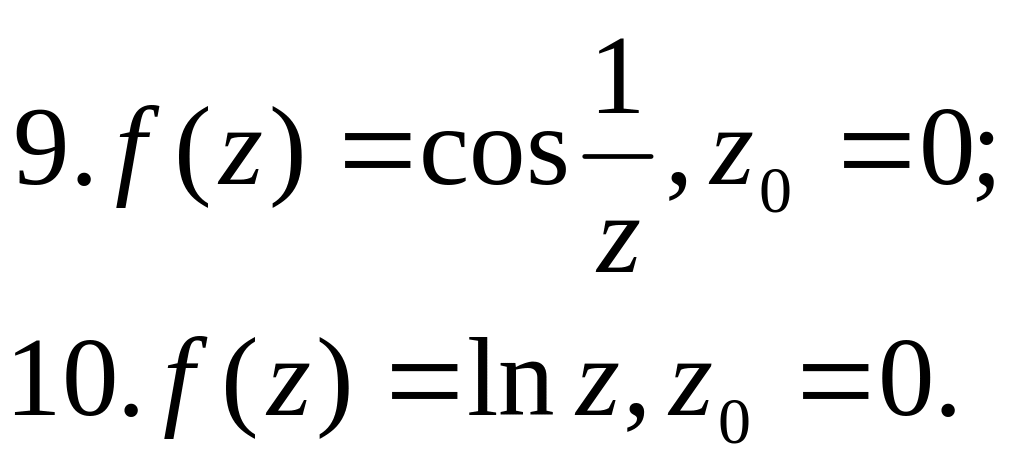- •Змістовний модуль №1. Комплексні числа та їх геометричне представлення
- •Комплексні числа. Форми запису комплексного числа. Дії над комплексними числами
- •1.2. Послідовності і ряди комплексних чисел. Степеневий ряд
- •Змістовний модуль №2. Похідна функції комплексної змінної
- •2.1 Функції із с в с. Границя, неперервність
- •2.2. Похідна функції комплексної змінної. Умови диференційованості
- •2.3. Геометричний зміст модуля і аргументи похідної комплексної функції
- •2.4. Означення аналітичної функції. Поняття Конформного відображення
- •Змістовний модуль №3. Елементарні аналітичні функції
- •Лінійна функція
- •Дробово-лінійна функція
- •Степенева функція. Поверхня Рімана
- •Функція Жуковского
- •Показникова функція комплексної змінної
- •Тригонометричні функції
- •Логарифмічна функція. Точка розгалуження
- •Радикал. Загальна степенева функція
- •Обернені тригонометричні функції
- •Змістовний модуль №4. Інтеграл функції комплексної змінної
- •Інтеграл від функції комплексної зміної по кусочно-гладкому контуру
- •Теорема Коші
- •Невизначений інтеграл. Формула Ньютона-Лейбница
- •Змістовний модуль № 5. Інтегральна формула Коші та її наслідки
- •5.1. Формула Коші. Принцип максимума модуля
- •5.2. Цілі функції. Теорема Ліувіля. Основна теорема алгебри
- •5.3. Розкладання функції в ряд Тейлора. Оцінка коефіцієнтів степеневого ряду
- •5.4. Нулі аналітичної функції. Ізольованість нулів. Теорема єдиності
- •5.5. Аналітичне продовження. Елементарні функції як аналітичні продовження
- •Змістовний модуль № 6. Ізольовані особливі точки аналітичних функцій
- •6.1. Розкладання аналітичної функції в ряд Лорана
- •6.2. Класифікація ізольованих особливих точок. Нескінченно віддалена особлива точка. Критерій особливої точки, яка усувається
- •6.3. Критерій полюса
- •6.4. Теорема Сохоцького-Вейєрштрасса
- •6.5. Раціональні і міроморфні функції
- •Змістовний модуль № 7. Лишки та їх застосування
- •7.1. Означення ЛишкА. Обчислення лишків
- •7.2. Основна теорема теорії лишків
- •7.3. Застосування теореми лишків до обчислення визначених інтегралів
- •Контрольні роботи Контрольна робота №1 (денна форма навчання)
- •Контрольна робота №2 (денна форма навчання)
- •Контрольна робота (заочна форма навчання)
- •Зразки розв'язування задач
- •Література
5.4. Нулі аналітичної функції. Ізольованість нулів. Теорема єдиності
Означення2.
Нехай
аналітична в області
.
Точка
називається нулем
,
якщо
![]() .
.
Нехай
розкладається в околі
в ряд
,
тоді якщо
![]() – нуль
,
то
– нуль
,
то
![]() .
Якщо
.
Якщо
![]() ,
– називається нулем порядку k.
,
– називається нулем порядку k.
Якщо
– нуль
порядку k, то
![]() ,
де
,
де
![]() -
аналітична функція в околі
і
не є нулем функції
.
-
аналітична функція в околі
і
не є нулем функції
.
Теорема6.
Нехай
аналітична в області
і обертається в нуль в різноманітних
точках
![]() . Якщо послідовність
сходиться до
. Якщо послідовність
сходиться до
![]() ,
,
![]() в області
.
в області
.
Доведення теореми див. [2. с.263], [1, с.72].
Наслідок 1. Нулі аналітичних функцій – ізольовані точки.
Наслідок
2.
Нехай
аналітична в області
,
тоді в будь-якій обмеженій замкненій
підобласті
![]() функція
має скінчене число нулів.
функція
має скінчене число нулів.
Наслідок з теореми являє собою теорему єдиності:
Теорема7.
Нехай
і
аналітичні в
.
Якщо в
існує деяка підпослідовність різноманітних
точок
,
що сходиться до деякої точки
![]() ,
в яких
,
в яких
![]() і
співпадають, то
і
співпадають, то
![]() в
.
в
.
З теореми єдиності легко отримати:
Наслідок 1: Якщо і аналітичні в і співпадають на деякій кривій, що належить , то .
Наслідок
2:
Якщо
![]() ,
,
![]() аналітичні в
аналітичні в
![]() ,
відповідно і
,
відповідно і
![]() ,
область така, що
,
область така, що
![]() ,
то існує єдина аналітична функція
,
то існує єдина аналітична функція
![]()
Приклад1.
Визначити нулі та їх порядок
![]() .
.
Розв’язання.
Нулями є точки
![]() .
Покажемо, що нулі мають порядок 1. Дійсно,
.
Покажемо, що нулі мають порядок 1. Дійсно,
![]() для нуля
для нуля
![]() ,
,
![]() та
та
![]() ,
тобто 3і – нуль першого порядку. Аналогічно
для
,
тобто 3і – нуль першого порядку. Аналогічно
для
![]() .
.
Вправи
Знайти порядок нуля z=0 для функцій:
|
|
5.5. Аналітичне продовження. Елементарні функції як аналітичні продовження
Нехай
аналітична в
![]() та
та
![]() .
Розкладемо
в степеневий ряд в околі точки
:
.
Розкладемо
в степеневий ряд в околі точки
:
![]() .
.
Тоді можливі два випадки:
1) радіус
збіжності ряду не більший відстані від
до границі області
![]() .
.
В цьому
випадку розклад не виводить первісну
аналітичну функцію за межі області
![]() .
.
2) радіус збіжності ряду більший за відстань від до границі
Нехай
![]() – коло збіжності ряду,
– коло збіжності ряду,
![]() та
та
![]() ,
причому аналітична функція
,
що задана рядом в
співпадає з
в середині
,
причому аналітична функція
,
що задана рядом в
співпадає з
в середині
![]() ,
тобто говорять, що
,
тобто говорять, що
![]() є аналітичним продовженням
є аналітичним продовженням
![]() в
в
![]() .
Причому, за теоремою про єдиність, це
продовження єдине. Міркуючи аналогічно
для деяких
.
Причому, за теоремою про єдиність, це
продовження єдине. Міркуючи аналогічно
для деяких
![]() і т.д. отримаємо аналогічне продовження
вздовж ланцюга
і т.д. отримаємо аналогічне продовження
вздовж ланцюга
![]() .
Будуючи різноманітні ланцюги областей,
що виходять за
,
ми отримаємо аналітичне продовження
.
Будуючи різноманітні ланцюги областей,
що виходять за
,
ми отримаємо аналітичне продовження
![]() на область, що містить
.
на область, що містить
.
Означення3. Функція F(z), отримана шляхом аналітичного продовження вздовж різноманітних ланцюгів, що виходять з області , первинного задання , називається повним аналітичним продовженням функції .
Розглянемо ряди
![]() .
.
Степеневі
ряди сходяться по всій
-
площині. Крім цього,
![]() ,
,
![]() -
задані по всій площині і є аналітичними,
причому,
-
задані по всій площині і є аналітичними,
причому,
![]() ,
,
![]() для
для
![]() і по теоремі єдиності
і по теоремі єдиності
![]()
![]() ,
тобто
,
тобто
![]() ,
,
![]() -
аналітичні продовження
-
аналітичні продовження
![]() ,
,
![]() з дійсної осі.
з дійсної осі.
Більш детально див. [1, 2, 3].
Змістовний модуль № 6. Ізольовані особливі точки аналітичних функцій
6.1. Розкладання аналітичної функції в ряд Лорана
Теорема1.
Нехай
![]() аналітична в кільці
аналітична в кільці
![]() ,
тоді вона в цьому кільці однозначно
визначена рядом Лорана, що збігається
,
тоді вона в цьому кільці однозначно
визначена рядом Лорана, що збігається
![]() .
.
Доведення теореми див. [2, с.282], [1, с.110].
Приклад1.
Розкласти в ряд функцію
![]()
Розв’язання.
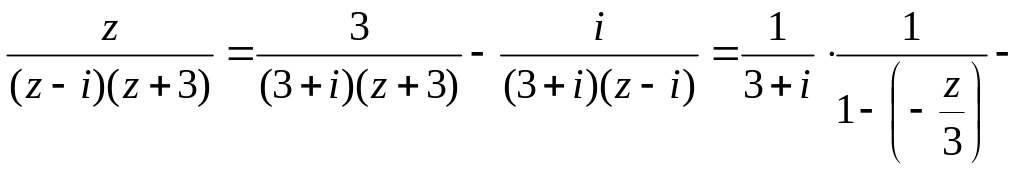

Вправи
Розкласти в ряд Лорана в околі точки
|
|