3.3.2. Значения моментов инерции некоторых тел

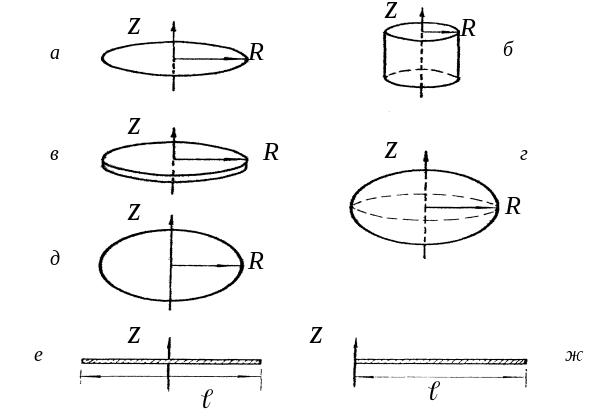
Рис. 3.14. Моменты инерции некоторых тел

1. Момент инерции обруча (рис. 3.14, а) радиусом R и массой m относительно оси Z, перпендикулярной плоскости обруча и проходящей через центр инерции обруча, равен

. (3.31)

Если ось Z совпадает с диаметром обруча, то момент инерции будет равен

. (3.32)

2. Момент инерции полого тонкостенного цилиндра (рис. 3.14, б) радиусом R и массой m относительно оси Z, совпадающей с продольной осью симметрии цилиндра, равен

. (3.33)

3. Момент инерции сплошного диска (рис. 3.14, в) радиусом R и массой m относительно оси, перпендикулярной плоскости обруча и проходящей через центр инерции диска, равен

. (3.34)

Если ось Z совпадает с диаметром диска (рис. 3.14, д), то момент инерции будет равен

. (3.35)

4. Момент инерции сплошного шара (рис. 3.14, г) радиусом R и массой m относительно оси Z, проходящей через центр инерции шара, равен

. (3.36)

5. Момент инерции тонкого прямого стержня (рис. 3.14, е) длиной и массой m относительно оси Z, проходящей через центр инерции стержня, равен

. (3.37)

Если ось Z проходит через конец стержня (рис. 3.14, ж), то момент инерции тонкого прямого стержня длиной и массой m равен

. (3.38)

Примеры расчетов моментов инерции

1. Момент инерции стержня относительно оси, проходящей через конец стержня (рис.3.15).

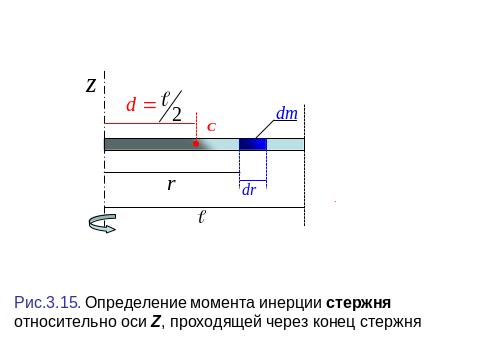
Линейная плотность массы стержня

,

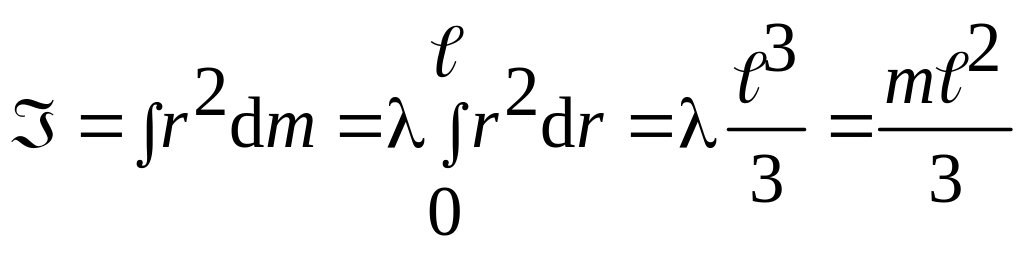. (3.39)

Чтобы найти момент инерции стержня относительно оси, проходящей через точку С (центр инерции) _С, применим теорему Штейнера:  = _С + md ². Здесь .

Тогда

_С =  – md² = .

2. Момент инерции обруча относительно оси, проходящей через центр инерции (точку С) обруча перпендикулярно его плоскости (рис.3.16).

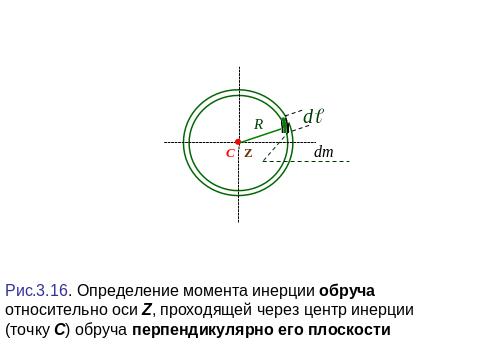
Линейная плотность массы образца

.

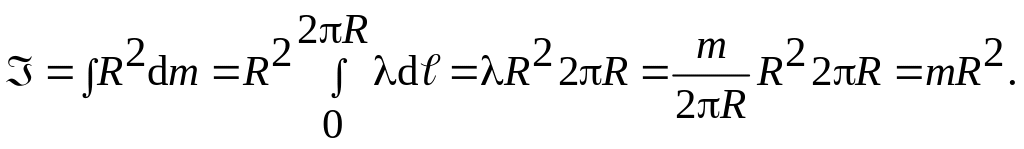(3.40)

3. Момент инерции диска относительно оси, проходящей через центр инерции (точку С) перпендикулярно плоскости диска (рис.3.17).

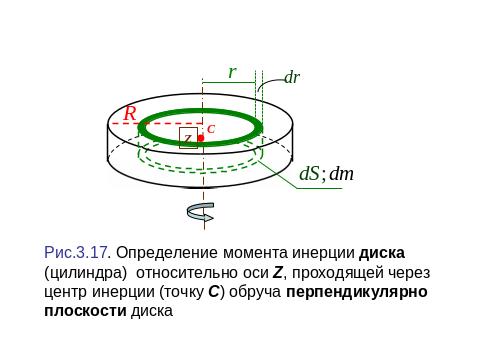
Поверхностная плотность массы диска:

dS = 2rdr,

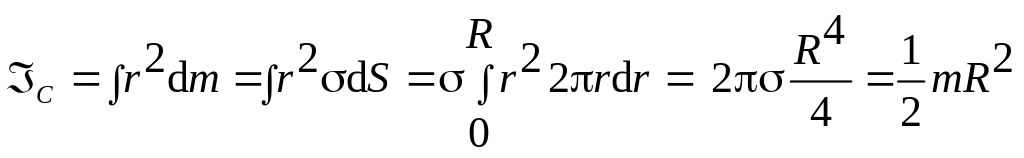. (3.41)

4. Момент инерции шара относительно оси, проходящей через центр инерции (рис.3.18).

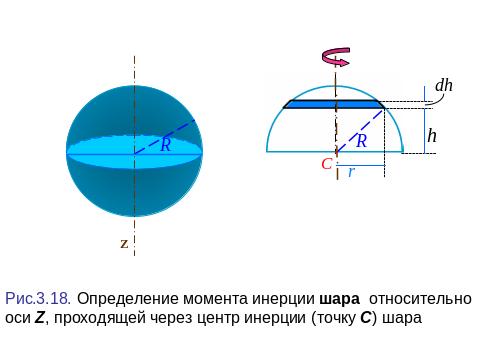
объемная плотность массы шара

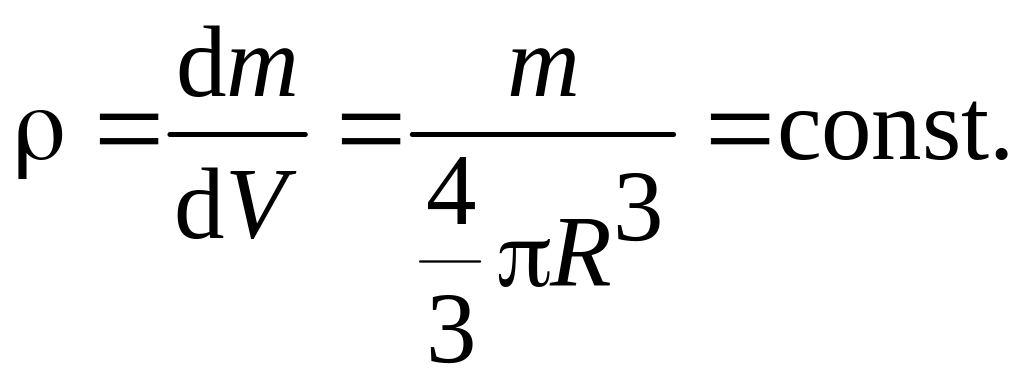
Разрежем половину шара на диски масса каждого – dm, объем – dV = r²dh, толщина – dh → 0 и радиус – r.

,

тогда

.

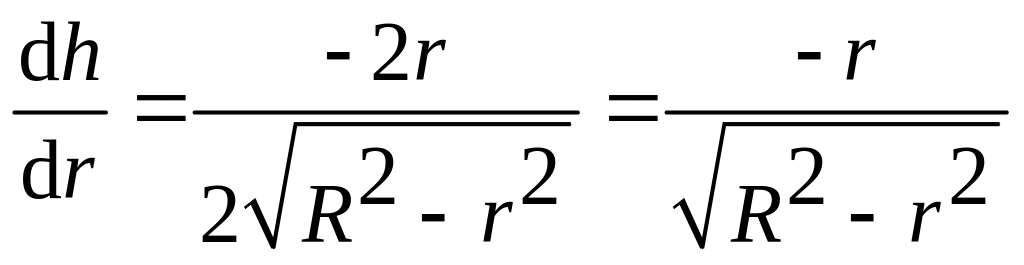Моменты инерции таких дисков

. (3.42)

Момент инерции половины шара получится как результат непрерывного суммирования (интегрирования) этих моментов инерции:

.

.

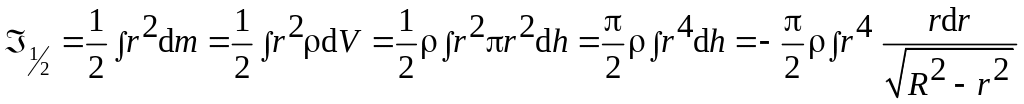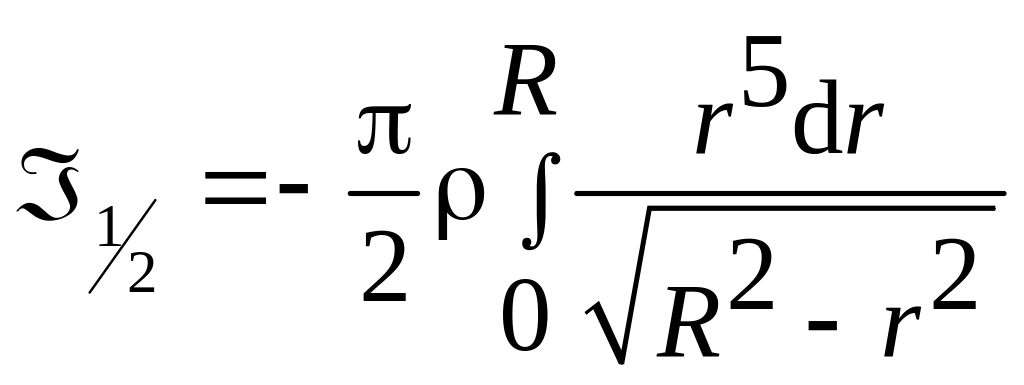Момент инерции шара в целом относительно центра инерции – точки С:

_C = 2 _,

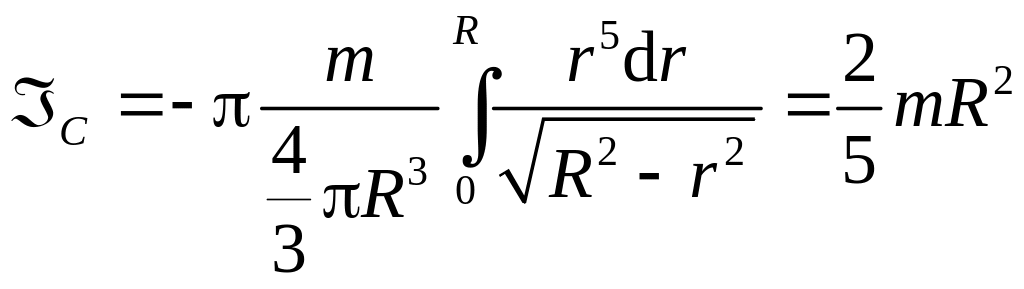. (3.43)

3.3.3. Осевой момент импульса

вектор осевого момента импульса параллелен вектору угловой скорости, направлен по оси вращения и определяется по формуле

, (3.44)

где  – момент инерции тела относительно оси Z (рис. 3.19); – угловая скорость твердого тела относительно оси Z; – аксиальный вектор.

Основные свойства осевого момента импульса:

1. Момент импульса является аксиальным вектором, направление которого находится по правилу правого винта. Вектор можно разложить, в случае необходимости, по координатным осям.

2. Момент импульса системы твердых тел определяется векторной суммой моментов импульса каждого тела.

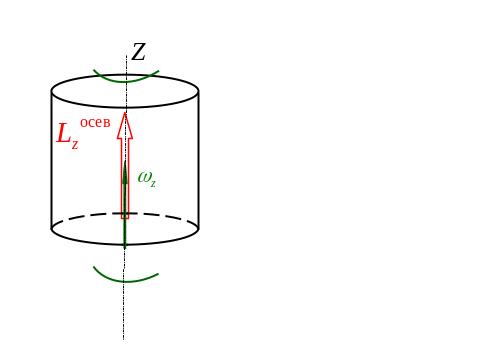
Рис. 3.19. Осевое вращение а.т.т.