8.2. Интегральные соотношения и расчет пограничного слоя

Соотношение Кармана. Рассмотрим двухмерное установившееся движение жидкости в пограничном слое. Выберем два сечения пограничного слоя, проведенные нормально к обтекаемой поверхности на расстоянии Δх (рис. 76). Применим теорему об изменении количества движения к объему жидкости, ограниченному контуром ABCD и имеющему единичную толщину. Уравнение импульсов (2.21) имеет вид:

(8.5)

или в проекции на ось x:

(8.5a)

где f – результирующая всех сил, приложенных к объему. Жидкость втекает в выделенный неподвижный объем через левую и верхнюю грани и вытекает через правую, в результате чего устанавливается некоторый баланс в обмене количеством движения.

Вычислим количество движения, поступающее в выделенный объем через грань АВ. Через элементарную полоску этой грани с основанием dy и высотой, равной единице, протекает за время Δt масса жидкости, равная ω_xdyΔt, через всю грань АВ поступает масса . Элементарная массаω_xdyΔt несет количество движения, проекция которого на ось x равна , Интегрируя это выражение по у от у = 0 до у = δ, получаем:

.

Приращение количества движения от грани AB до грани CD составит

.

Вычислим далее количество движения, поступающее в выбранный объем через верхнюю грань BC. Пусть скорость потока на верхней границе слоя равна U. Масса Δm жидкости, поступающей с этой скоростью в пограничный слой извне,

Рис.76

равна разности масс: поступившей внутрь объема ABCD через грань AB и вытекшей через грань CD, т. е.

.

Количество движения, поступающего через грань BC, равно

,

и левая часть уравнения (8.5a) принимает вид:

Рассмотрим теперь силы, действующие на выделенный объем. Внешние объемные силы (например, силы тяжести) в пограничном слое намного слабее силы трения, поэтому будем ими пренебрегать. Чтобы определить проекцию действующих сил на ось x, нужно учесть: силу давления на грань AB, равную рδ; силу давления грань СО, равную (р + Δр) (δ + Δδ), где Δр – приращение давления от грани AB до грани CD, а Δδ – приращение толщены пограничного слоя от грани AB до грани CD; силу давления на грань BC, равную рΔδ; и силу трения, равную – τΔx, где τ – сила трения на единицу площади обтекаемой поверхности. Суммирую эти силы, получим

.

Подставляя полученные величины в уравнение импульсов (8.5а), разделив на Δчx: и переходя к пределу при , имеем

. (8.6)

Уравнение (8.6) называется уравнением импульсов или интегральным соотношением Кармана (1921) для плоского установившегося течения в пограничным слое.

Если, как и в § 8.1, выразить с помощью уравнения Бернулли продольный градиент давления через распределение скоростей U во внешнем невозмущенном потоке, т.е.

,

то уравнение Кармана перепишется в виде:

. (8.6a)

При выводе уравнение импульсов (8.6) мы не делали никаких предположений относительно природы карательного напряжения τ, поэтому оно в одинаковой степени применимо как к ламинарному, так и к турбулентному пограничному слою.

В уравнение импульсов предполагается известным распределение скоростей во внешнем потоке, т. е. величины U и ; они могут быть определены методами гидродинамики идеальной жидкости или опытным путем в результате измерения распределения давления на поверхности обтекаемого тела. Неизвестные величины – ω_x, δ и τ, а в случае сжимаемой жидкости еще и ρ. Поэтому для определения наиболее важных для практики характеристик пограничного слоя – его толщины δ и касательного напряжения на стенке τ – приходится задаваться распределением скоростей в слое. То обстоятельство, что скорость ω_х внутри слоя входит в уравнение импульсов под знаком интеграла, уменьшает погрешность расчета и позволяет пользоваться приближенными законами распределения скорости.

Условные толщины пограничного слоя. Приведем еще одну форму записи уравнения импульсов, получаемую из выражения (8.6а) путем тождественных преобразований. Так как

,

то уравнение (8.6) может быть представлено в виде:

с .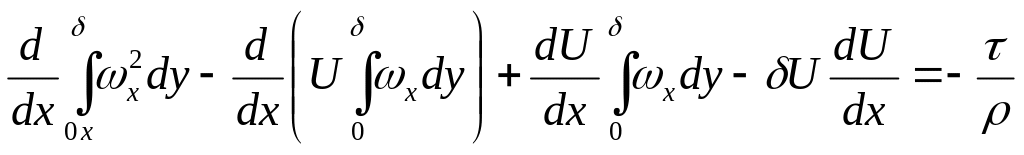

Рис. 77

Объединяя в последнем выражении члены, содержащие производные от интегралов, получим

. (8.6б)

Интеграл во втором слагаемом левой части уравнения (8.6б) представляет собой разность между расходами жидкости в пограничном слое, если бы скорость во всем его сечении не уменьшалась вследствие вязкости, а оставалась равной U, и действительным расходом (рис. 77). Таким образом, этот интеграл представляет собой уменьшение расхода в пограничном слое вследствие вязкости. Графически он изображен площадью с перекрестной штриховкой на рис. 77. Разделив этот интеграл на величину скорости U, получим некоторый размер δ*, равный толщине слоя, через который протекал бы недостающий расход:

.

На расстояние δ* оттесняются от поверхности тела линии тока невозмущенного течения вследствие торможения в пограничном слое. Поэтому δ* носит название толщины вытеснения.

Аналогично интеграл в первом слагаемом левой части уравнения (8.6б) можно рассматривать как уменьшение количества движения жидкости, протекающей через пограничный слой, или потерю импульса. Разделив этот интеграл на U², получим линейную величину δ**, называемую толщиной потери импульса:

.

Вводя величины δ* и δ** в уравнение (8.6б), получим

или, выполнив дифференцирование и разделив на U²,

. (8.6в)

В этой форме записи уравнения импульсов неизвестными являются δ*, δ** и τ.

Ламинарный пограничный слой на плоской пластинке. При продольном обтекании тонкой плоской пластинки скорость внешнего потока не меняется по длине x; члены в уравнениях Прандтля (8.1а) и в уравнении Кармана (8.6а) равны нулю. Поэтому основные параметры пограничного слоя на пло­ской пластинке определяются наиболее просто. Результаты этого расчета часто используются для приблизительного определения параметров пограничного слоя различных удобообтекаемых тел – тонких крыльев и др.

Применим для расчета пограничного слоя на плоской пластинке уравнение импульсов (8.6а). Будем считать жидкость несжимаемой. Если постоянная скорость внешнего потока равна ω_∞, то уравнение импульсов приобретает вид:

(8.7)

или

. (8.7a)

Наиболее простой способ задания скорости в ламинарном пограничном слое – это представление ω_x в виде степенного ряда по степеням y:

Коэффициенты этого ряда а₀(x), а₁(x)... можно определить из граничных условий (8.2) – (8.5), которым должна удовлетворять скорость ω_x и ее производные на границах слоя. Эти условия таковы:

(8.8)

Для простоты ограничимся в разложении ω_x первыми двумя членами, т. е. ω_x = а₀ + a₁y. Предположение о линейном распределении скоростей по толщине пограничного слоя является, конечно, очень грубым приближением, но мы убедимся ниже, что даже такое приближение дает удовлетворительные результаты. Используя первые два из граничных условий (8.8), получим

т. е.

.

Касательное напряжение τ на поверхности пластинки опреде­ляется по закону Ньютона (1.4а), т. е.

;

в данном случае имеем

.

Для определения толщины пограничного слоя δ подставим полученные величины в уравнение импульсов (8.7). Для этого вычислим входящие в него интегралы:

;

.

Подставляя эти величины в уравнение (8.7), имеем

,

или

.

Это дифференциальное уравнение с разделяющимися переменными; запишем его в виде:

.

Интегрируя это уравнение, получаем

.

Постоянную интегрирования находим из условия на передней кромке пластинки. Полагая, что при x = 0 пограничный слой только начинает развиваться, т. е. δ |_x=0 = 0, имеем С = 0; следовательно,

,

где – местное число Рейнольдса. Касательное напряжение τ получается равным

.

Полученные формулы для δ и τ отличаются от точных формул, являющихся результатом более сложного решения уравнений Прандтля (8.1), только числовыми коэффициентами. Точные решения имеют вид:

; (8.9)

(8.10)

(в точном решении за толщину пограничного слоя принималось такое расстояние, от стенки, где скорость отличается всего на 1% от скорости невозмущенного потока). Величины δ и τ могут быть вычислены гораздо точнее, если не ограничиваться двумя слагаемыми в разложении ω_x по степеням y, а взять три или четыре слагаемых; результаты решения в этом случае быстро сходятся к точным формулам (8.9) и (8.10).

Решение для пластинки показывает, что в ламинарном пограничном слое его толщина δ нарастает по длине пластинки по параболическому закону, а напряжения трения обратно пропорционально (рис. 78). Этот закон при x = 0 дает τ = ∞; в действительности напряжение трения у входной кромки не может возрастать безгранично, так как у реальной пластинки (а не бесконечно тонкой) происходит торможение у входной кромки из-за ее конечной толщины . Следовательно, в передней критической точке и . Поэтому действительное распределение касательных напряжений на поверхности пластинки будет таким, как показано на рис. 78 пунктирной линией. Величина участка, к которому не применима формула (8.10), зависит от степени заостренности входной кромки пластинки.

Рис. 78

Определим полную силу трения на поверхности пластинки длиной l и шириной b при ламинарном обтекании. Используя выражение (8.10), получим, что сила трения на одной из сторон пластинки равна:

.

Сравнивая полученный результат с общей формулой для определения гидродинамических сил (8.5), которая для сил трения может быть записана в виде:

,

где С_тр – коэффициент трения; F = bl – площадь обтекаемой поверхности, получим для ламинарного пограничного слоя на пластинке:

,

где – местное число Рейнольдса для x = l. Следовательно, коэффициент сопротивления С_тр для ламинарного слоя на пластинке равен:

(8.11)

Турбулентный пограничный слой на плоской пластинке. Применим уравнение импульсов (8.7) для расчета турбулентного пограничного слоя на пластинке. Для этого, как уже отмечалось выше, требуется задать хотя бы приближенно закон распределения скоростей поперек слоя и характер зависимости τ от U и δ. Наиболее просто эти дополнительные условия задаются, если считать распределение скоростей в турбулентном пограничном слое таким же, как и распределение скоростей по радиусу цилиндрической трубы.

Согласно опытным данным в трубе при достаточно больших числах Рейнольдса осредненная скорость пропорциональна расстоянию от стенки в степени . Поэтому будем считать, что

Также из экспериментов с трубами следует, что зависимость касательного напряжения трения от δ и U имеет вид:

. (8.13)

Подставляя выражение (8.12) в уравнение импульсов на плоской пластинке (8.7), вычислим входящие в него интегралы:

;

.

С использованием полученных выражений и формулы (8.13) уравнение (8.7) приводится к виду:

или

.

Интегрируя полученное уравнение с разделяющимися переменными, получим:

.

Постоянную интегрирования C можно определить, если принять, что в критическом сечении, где ламинарный слой переходит в турбулентный, их толщины одинаковы, т. е. . Тогда начальное значение толщины турбулентного слоя можно определить с использованием теории ламинарного слоя (формула 8.9). Если же местные числа Рейнольдса очень велики (порядка 107 и больше), то ламинарный участок у входной кромки пластинки занимает относительно небольшую часть ее длины. В этом случае можно пренебречь его влиянием на толщину слоя и считать , откуда следует С = 0; получаем формулу для расчета толщины турбулентного слоя на пластинке в виде:

Отметим, что толщина турбулентного слоя пропорциональна x^4/5, т. е. она нарастает вдоль пластинки гораздо быстрее, чем в случае ламинарного пограничного слоя, где δ ~ x^1/2. Это объясняется тем, что в турбулентном слое вследствие перемешивания частиц торможением охватываются более толстые слои внешнего потока, чем в случае ламинарного слоя.

Подставляя значение δ из (8.14) в формулу (8.13), получим выражение для τ в турбулентном слое пластинки:

Рис. 79

.

Выражение (8.15) показывает, что в турбулентном слое τ убывает с удалением от входной кромки пропорционально , т. е. менее интенсивно, чем в случае ламинарного слоя, где . Распределение касательных напряжений τ по длине пластинки, на которой ламинарный пограничный слой переходит в турбулентный при x = x_кр, представлено на рис. 79.

Определим полную силу трения для пластинки длиной l и шириной b. Сила трения на одной стороне пластинки равна:

,

отсюда коэффициент трения

,

или

. (8.16)

При числах Рейнольдса до формула (8.16) находится в хорошем согласии с экспериментальными данными. При больших значениях Re_l значения C_{тр. т} получаются несколько заниженными.

Наряду со степенным заданием скорости в турбулентной слое (8.12) уравнение импульсов (8.7) интегрируется также при логарифмическом распределении скоростей в пограничном слое:

;

такой способ задания скорости является универсальным для более широких значений Re_l (от 10⁶ до 10⁹). Использование логарифмического закона приводит к следующей формуле для C_{тр. т}:

.

При не слишком больших значениях Re_l последняя формула дает результаты, практически совпадающие с расчетом по (8.16).

Факторы, влияющие на турбулизацию пограничного слоя. Рассмотрим явление турбулизации пограничного слоя в аналогии с переходом течения в трубе из ламинарного в турбулентное. При равномерном течении в трубе в ее поперечном сечении, как и в пограничном слое, происходит нарастание скорости от стенки к оси (например, для ламинарного течения эпюра скоростей была показана на рис. 17). Поэтому толщину пограничного слоя можно считать аналогичной радиусу трубы

и можно вычислять число Рейнольдса по толщине пограничного слоя:

.

Опыт показывает, что критическое число Рейнольдса Re_{δ кр} на пластинке оказывается в среднем близким к для трубы. Это обстоятельство говорит о том, что потеря внутренней, устойчивости ламинарного движения в трубе и в пограничном слое имеет одинаковую природу.

Имеются, однако, и существенные различия между этими явлениями.

В трубе величина Re_кр практически не зависит от начальных возмущений, вносимых в поток на входном участке трубы; эти возмущения затухают в ламинарном течении, и только потеря внутренней устойчивости при Re > Re_кр приводит к появлению пульсационных движений. В пограничном слое, наоборот, положение точки перехода существенно зависит от интенсивности турбулентных движений в набегающем потоке. Это связано с тем, что через внешнюю границу пограничного слоя в него непрерывно поступают возмущения из внешнего потока. При повышении степени возмущенности этого потока величина критического числа Рейнольдса уменьшается, точка перехода смещается навстречу течению. Таким образом, увеличение интенсивности пульсаций во внешнем потоке способствует ранней турбулизации пограничного слоя.

В трубе величина Re_кр не зависит от степени шероховатости стенок: при ламинарном течении скорость вблизи стенки равна нулю, и выступы шероховатости лежат в застойной области. В случае пограничного слоя у входной кромки пограничный слой только начинает развиваться ( ), и бугорки шероховатости высовываются из пограничного слоя, внося в него возмущения. Поэтому повышение степени шероховатости способствует ранней турбулизации пограничного слоя и увеличению сопротивления трения. Это явление особенно сильно сказывается при больших, скоростях обтекания, поэтому увеличение скоростей (в авиации, турбиностроении и т. д.) предъявляет повышенные требования к чистоте обработки обтекаемой поверхности, особенно вблизи входной кромки.

Величина критического числа Рейнольдса и связанная с ней координата точки перехода x_кр зависит также от того, является ли течение конфузорным. Повышение скорости вниз по течению в конфузорном канале угнетает развитие пограничного слоя и способствует его ламинизации, .величина критического числа Рейнольдса возрастает. Наоборот, переход к диффузорному течению способствует ранней турбулизации пограничного слоя. Например, на спинке крыла самолета или лопатки турбомашины имеется входной конфузорный участок, где скорость возрастает с координатой x; здесь пограничный слой, как правило, ламинарный. В задней части крыла поток диффузорный и пограничный слой турбулентен. Точка перехода обычно очень близка к сечению, в котором . Величина продольного градиента скорости оказывает также существенное влияние на явление отрыва пограничного слоя, рассмотренное ниже.