8.1. Общие понятия и дифференциальные уравнения пограничного слоя

Понятие пограничного слоя. Как уже отмечалось выше, при движении с большой скоростью в маловязких жидкостях или газах удобообтекаемых тел действие вязкости сосредоточено в тонком пристенном слое – пограничном слое. Поэтому при интегрировании уравнений движения вязкой жидкости нет необходимости распространять их на все пространство, занятое потоком, достаточно применить их лишь к области быстрого изменения скорости.

Опыт показывает, что толщина пограничного слоя весьма мала по сравнению с размерами обтекаемого тела. Так, например, при продольном обтекании пластинки потоком воздуха со скоростью 100 м/сек на расстоянии 1 м от входной кромки скорость на поверхности пластинки равна нулю, а на расстоянии 15 мм от поверхности она практически равна 100 м/сек и не изменяется при дальнейшем удалении. Из-за малых градиентов скорости во внешнем потоке силы вязкости там пренебрежимо малы; движение в этой области подчиняется законам динамики идеальной жидкости.

Исходя из этих соображений, при обтекании тел маловязкой жидкостью и при большой скорости потока ω_∞ пространство, занятое потоком, можно условно разбить на три области, которые мы рассмотрим применительно к обтеканию крыла (рис. 74).

Первую область занимает пограничный слой, в котором скорость течения меняется от нуля на поверхности тела до скорости невозмущенного потока на границе слоя. Для наглядности на рис. 74 масштаб для поперечных размеров выбран более крупным, чем для продольных; в действительности пограничный слой имеет меньшую толщину. Вторая область – аэродинамический след, или спутная струя, – содержит частицы пограничного слоя, унесенные потоком. Третья область – это остальное пространство, занятое потоком, в котором жидкость можно считать идеальной, а движение – происходящим без вращения частиц, т. е. потенциальным.

Уравнения Прандтля. При выводе дифференциальных уравнений пограничного слоя выберем систему координат, как показано на рис. 74: ось x направлена вдоль обтекаемой поверхности, ось y всюду к ней перпендикулярна. Начало координат – в передней критической точке, где раздваивается набегающий поток. В силу малой толщины пограничного слоя δ, по сравнению с размерами обтекаемого тела, можно пренебречь кривизной поверхности и рассматривать выбранную систему координат как обычную декартову.

Рис. 74

Будем считать жидкость несжимаемой, а движение – установившимся. Для плоского (двухмерного) потока система уравнений Навье–Стокса (7.1) имеет вид:

;

.

В силу сделанных предположений внутри пограничного слоя значительны градиенты только продольной составляющей скорости ω_x; поэтому второе из записанных уравнений принимает вид:

.

Из него следует, что давление внешнего потока передается через пограничный слой без изменений. Легко показать также, что в первом уравнении член пренебрежимо мал по сравнению с членом . В итоге первое уравнение и записанное совместно с ним уравнение неразрывности (2.7) образуют систему:

; (8.1)

.

Отметим, что полная производная скорости ω_х (х, у, t) по времени, стоящая в левой части первого уравнения системы (8.1), по правилу дифференцирования функции нескольких переменных равна

(так как ) Поэтому при установившемся движении ( ) система (8.1) может быть представлена в виде системы уравнений Прандтля (1904):

(8.1a)

Уравнения Прандтля значительно проще, чем исходные уравнения Навье–Стокса (7.1). Вместе с тем, они достаточно хорошо соответствуют действительности, и результаты их интегрирования весьма точно совпадают с данными эксперимента.

Продольное изменение давления (член ) в уравнениях

Прандтля может быть выражено через распределение скоростей во внешнем неискаженном потоке. Действительно, если скорость внешнего потока у данной точки обтекаемого тела равна U, то согласно уравнению Бернулли для идеальной несжимаемой жидкости

.

Дифференцируя последнее равенство по x, получаем

или

,

и система (8.1а) приобретает вид:

Распределение скоростей во внешнем потоке, входящее в первое уравнение системы (8. 16), может быть получено в результате решения задачи об обтекании тела потоком идеальной жидкости, например методом ЭГДА. Таким образом осуществляется «стыковка» двух основных теоретических разделов гидроаэромеханики – динамики идеальной и вязкой жидкости.

Граничные условия. Одно из граничных условий решения системы (8.1) требует равенства нулю вектора скорости на поверхности обтекаемого тела:

. (8.2)

Второе условие предусматривает отсутствие торможения на внеш­ней границе пограничного слоя. Оно может задаваться двояким образом. Строго говоря, влияние пристенного торможения должно сказываться на любом расстоянии от стенки, поэтому при строгой постановке задачи второе условие задается в виде:

. (8.3)

Решение этой задачи позволяет определить параметры «асимптотического» пограничного слоя, в котором распределение скоростей в пограничном слое асимптотически переходит в распределение скоростей во внешнем потоке. Более часто второе граничное условие задается для пограничного слоя конечной толщины, под которым понимают слой, где полное изменение скорости происходит на расстоянии конечной толщины пограничного слоя δ, от нуля на стенке до ω_x = U на внешней границе, т. е. второе граничное условие имеет вид:

(8.3a)

В качестве δ можно, например, принимать расстояние от стенки, на котором скорость отличается на 1% от скорости невозмущенного потока. Хотя такое задание граничного условия является менее строгим, тем не менее математически решение оказывается более простым, а результаты почти совпадают с решением более строгой задачи.

Турбулизация пограничного слоя. Опыт показывает, что слоистое, ламинарное течение жидкости в пограничном слое наблюдается лишь на начальном участке обтекаемой поверхности. При достаточно больших размерах обтекаемого тела на некотором расстоянии от передней критической точки наблюдается перестроение ламинарного течения в турбулентное, в котором движение носит неустановившийся пульсационный характер. Критическая точка на поверхности тела, где начинается переход ламинарного течения внутри пограничного слоя в турбулентное, называется точкой перехода. Схема обтекания крыла с двумя видами пограничного слоя на нем представлена на рис. 75. Область 1 соответствует ламинарному пограничному слою, область 2 – турбулентному; точки Т_в и Т_н соответствуют началу перехода ламинарного пограничного слоя в турбулентный на верхней и нижней поверхностях крыла, в точке S происходит отрыв пограничного слоя. Область 3 – аэродинамический след за телом, область 4 – внешний невозмущенный поток.

Обычно предполагают, что в непосредственной близости от обтекаемой поверхности пульсации скорости сдерживаются этой поверхностью и движение здесь ламинарное. Это – так называемый ламинарный подслой, аналогичный подслою при движении жидкости в трубах в области гидравлически гладкого сопротивления (см. § 3.1). Но толщина этого подслоя настолько мала, что на рис. 75 он не показан. В случае достаточно крупных выступов шероховатости на обтекаемой поверхности ламинарный подслой вообще разрушается.

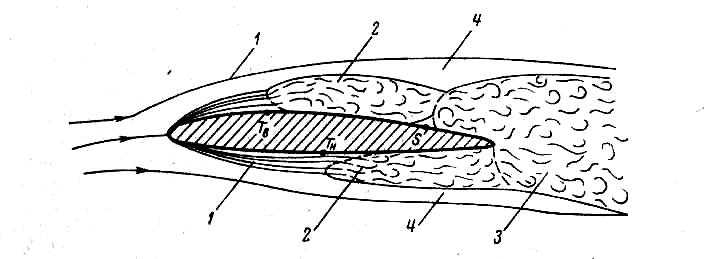
Рис. 75

Перестроение режима течения в пограничном слое зависит от величины местного числа Рейнольдса

,

где х – расстояние от передней критической точки. В частности, согласно экспериментальным данным при продольном обтекании пластинки точка перехода лежит при значениях x_кр, соответствующих в среднем критическому числу Рейнольдса

. (8.4)

Уравнения Прандтля (8.1) выведены в предположении, что трение в пограничном слое происходит только за счет вязкости. Это предположение справедливо для ламинарного пограничного слоя. При турбулентном течении обмен количеством движения между слоями происходит за счет взаимного проникновения вихревых частиц, размеры которых намного превышают размеры молекул. Поэтому обмен количеством движения резко возрастает и соответственно увеличивается сила трения. Механизм трения в турбулентном пограничном слое, как и в случае гидравлического сопротивления труб, зависит от величины числа Рейнольдса и шероховатости поверхности (см. рис. 16, § 3.1).

Дифференциальные уравнения Прандтля для решения задач турбулентного пограничного слоя применять невозможно. Для этого используется метод интегральных соотношений, предложенный Карманом; он более прост, чем интегрирование дифференциальных уравнений Прандтля, и поэтому применяется также и в задачах ламинарного пограничного слоя. Способ Кармана не позволяет определить поле скоростей в пограничном слое, однако он дает возможность вычислить толщину пограничного слоя и распределение сил трения по поверхности обтекаемого тела с достаточной для практики точностью, и гораздо проще, чем пои интегрировании дифференциальных уравнений.