5.5. Условия равновесия частично закрепленного тела

В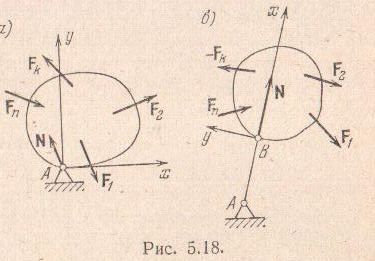 некоторых случаях приходится рассматривать равновесие частично закрепленных тел, т.е. тел, на которые наложены связи, допускающие некоторое перемещение тела. Очевидно, что при произвольной системе активных сил , приложенных к телу, равновесия не будет. Однако возможны и такие случаи, когда равновесие имеет место. Выясним условия, которым должны удовлетворять активные силы, чтобы тело находилось в равновесии. Прежде всего остановимся на случае твердого тела, имеющего неподвижную ось вращения; к телу приложена система активных сил, , расположенная в плоскости, перпендикулярной оси вращения. Ось вращения служит связью для рассматриваемого тела; согласно принципу освобождаемости действие связей заменяем реакцией , приложенной к точке А (предполагаем, что трение отсутствует).

Направление реакции зависит от характера приложенных к телу сил . Напишем уравнения равновесия в форме (5.18):

,

,

.

Из первых двух уравнений можно найти обе составляющие реакции . В последнее уравнение не входит. Это уравнение устанавливает зависимость межу активными силами, необходимую для равновесия тела.

Таким образом, для рассматриваемого случая активные силы должны удовлетворять одному уравнению

. (5.21)

Обратимся теперь ко второму примеру, где связью служит стержень. Направление реакции совпадает с осью стержня. Выбирая систему координат Вху, как указано на рис., имеем следующие уравнения равновесия:

,

,

.

Первое уравнение служит для определения реакции . Два других уравнения накладывают определенные требования на систему активных сил. Таким образом, для равновесия тела необходимо, чтобы активные силы в данном случае удовлетворяли двум условиям:

, . (5.22)

Последнее уравнение записано для точки тела В понятно, что его можно видоизменить, записав его для любой точки оси х.

5.6. Определение натяжения тяжелой подвешенной нити

З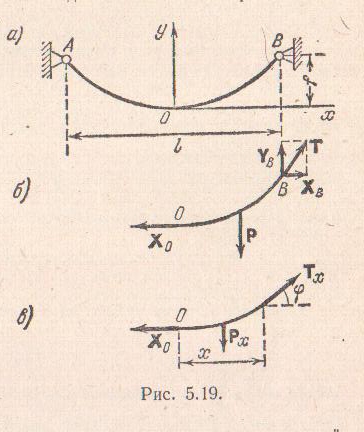 адача об определении натяжения в подвешенной тяжелой нити связана с проблемой прочности тросов или проводов линий электропередачи. Будем считать, что нить идеально гибкая и нерастяжимая и что провисание нити происходит только из-за различия между ее длиной L и расстоянием между опорами l.

Обозначим через q линейный удельный вес нити. Для пологой кривой можно принять, что вес равномерно распределен не по кривой АОВ, а по ее проекции АВ. Таким образом, общий вес нити будем считать равным ql.

В соответствии с аксиомой 5 можно рассматривать условия равновесия любой части нити. Рассмотрим, например, правую половину нити; действующие на нее силы изображены на рис. Заметим, что натяжение в любом сечении нити направлено по касательной к кривой в соответствующем месте (как это следует из предположения об идеальной гибкости нити). Поэтому в нижней точке нити О, принятой за начало координатной системы, натяжение горизонтально. Обозначив через f стрелу провеса (т.е. расстояние по вертикали между нижней точкой и опорами), запишем уравнение моментов относительно точки В

.

Здесь представляет собой вес половины нити. Из этого уравнения находим

; (5.23)

отсюда, между прочим, ясно, что чем меньше стрела провеса нити f, тем больше натяжение .

Из двух уравнений для проекций сил на оси можно найти составляющие натяжения нити в точке В

, ,

а затем и полное натяжение в точке В

.

Второе слагаемое в сумме под знаком корня значительно меньше единицы, и мы можем воспользоваться приближенной формулой

,

достаточной для таких малых значений . Тогда будет

. (5.24)

Этот результат определяет наибольшее натяжение нити, которое, впрочем, мало отличается от наименьшего натяжения .

Для вычисления и Т по найденным формулам необходимо знать стрелу провеса f, а для этого требуется располагать уравнением кривой, по которой провиснет нить. С этой целью рассмотрим часть нити, расположенную между началом координат и произвольным сечением с абсциссой х. Для этой части можно написать следующие уравнения равновесия (для проекций сил на оси х и у):

Здесь – вес рассматриваемой части нити, – натяжение на правом конце этой части.

Из первого уравнения можно заключить, что с удалением от нижней точки, т.е. с увеличением угла , натяжение нити возрастает и достигает максимума в точках подвеса.

Исключив из этих уравнений , получим с учетом формулы (5.23)

,

но , и мы приходим к дифференциальному уравнению, определяющему форму нити в положении равновесия:

. (5.25) Интегрируя его, получаем

.

Постоянную интегрирования С найдем из условия, что при ; отсюда следует

.

Таким образом, приближенно установлено, что тяжелая нить в положении равновесия принимает форму параболы^*. Теперь можно выразить стрелу провеса f через L и l. Для этого запишем известное из курса математического анализа выражение длины дуги

и заметим, что для пологой нити. Поэтому . Тогда будем иметь

. Подставляя сюда выражение (5.25), находим

;

отсюда получаем

. (5.26)

Задача 5.8. Определить наибольшее и наименьшее натяжение нити, если вес единицы длины составляет 10 кН, длина пролета м, а полная длина нити м.

Решение. Прежде всего по формуле (5.26) находим

м.

Наименьшее натяжение нити (в нижней части) определяется по формуле (5.23):

кН.

Наибольшее натяжение (в точках подвеса) находим по формуле (5.24):

кН.