4.3. Аналитическое определение главного вектора

и главного момента пространственной системы сил

Определим модули и направление векторов F_О и М_О. Пусть декартова система координат Охуz имеет начало в центре приведения О. Тогда проекции силы F_О на координатные оси найдутся из соотношений:

F_Ох= ∑ F_kх= F_1х+ F_2х+ … + F_пх,

F_Оу= ∑ F_kу= F_1у+ F_2у+ … + F_пу,

F_Оz= ∑ F_kz= F_1z + F_2z+ … + F_пz. (4.4)

Модуль силы F_О равен

, (4.5)

а направление определяется направляющими косинусами

, , . (4.6)

Для проекций вектора М_О имеем (см. (3.10))

,

,

. (4.7)

Следовательно, модуль и направление вектора М_О определяются формулами

, (4.8)

, , . (4.9)

При приведении пространственной системы сил к одной силе и одной паре сил угол между направлением главного вектора и направлением главного момента может получиться любым в зависимости от действующих сил. Для определения этого угла воспользуемся формулой, выражающей скалярное произведение векторов F_О и М_О:

F_О∙М_О= F_О М_О соs(F_О, М_О).

Отсюда

, (4.10) или, в соответствии с формулами (4.6) и (4.9),

(4.11)

В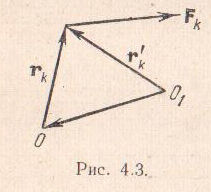 ыясним, как будет меняться сила и пара сил, к которым приводится рассматриваемая система сил, при перемене центра приведения. Так как сила F_О равна главному вектору, т.е. сумме всех сил системы, то для любого центра приведения она будет одной и той же. Если в качестве нового центра приведения взята точка О₁, то

(4.12)

Для центра приведения О₁ момент пары равен главному моменту относительно этого центра приведения

, (4.13)

где r'_k – радиус-вектор точки приложения силы F_k, проведенный из нового центра приведения О₁. Из рассмотрения рисунка видно, что

.

Подставив значение r'_k в формулу (4.13), получим

,

откуда на основании формул (4.2) и (4.3)

, (4.14)

т.е. момент пары, а следовательно, и главный момент при перемене центра приведения изменяются на момент силы, равной главному вектору, приложенному в старом центре приведения, относительно нового центра приведения.

Из формулы (4.14) следует, что если в каком-либо центре приведения, например, в точке О, F_О =0 и М_О =0, то и для любого центра приведения О₁ будет

F_О1=0, М_О1=0.

П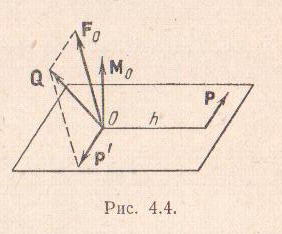 риведение произвольной системы сил к силе и паре сил не является единственным способом приведения к простейшему виду (хотя и применяется наиболее часто). Возможен и другой вариант приведения, согласно этому варианту система сил, как угодно расположенных в пространстве, может быть приведена к двум силам, в общем случае не лежащим в одной плоскости.

В самом деле, пусть произвольная система сил приведена в данном центре О к силе F_О и паре сил с моментом М_О. Выберем силы, составляющие пару равными Р и Р' (Р= – Р'); приложим одну из них (например, Р') в центре приведения и сложим ее с силой F_О. В результате получим силу Q = F_О+ Р', уже не лежащую в плоскости действия пары (Р, Р').

Таким образом, пространственная система сил приведена к двум силам Q и Р, которые в общем случае не лежат в одной плоскости.