3.6. Форсирующее звено (пропорционально - дифференцирующее)

Форсирующим называется звено, дифференциальное уравнение которого имеет вид

y = k1 u + k2 .

(3.32)

Как видим, его можно представить как сумму пропорционального и дифференцирующего звеньев.

Передаточная функция форсирующего звена,

,

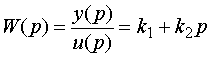записывается в стандартной форме

W(p) = k (1+Tp),

(3.33)

где k=k₁ - коэффициент передачи, T=k₂/k₁ - постоянная времени звена.

Определим теперь его переходную характеристику

h(t- )= 1(t- )+ (t- )

(3.34)

и импульсную функцию

g(t)= (t) = (t) + (t).

(3.35)

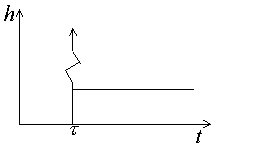
Рис.3.18. Переходная характеристика форсирующего звена

Запишем выражения для частотных характеристик.

АФХ: W(j )=k(1+jT );

(3.36)

ВЧХ: R( )=k

МЧХ: I( )=k ;

АЧХ: A( )= k ;

ФЧХ: ; ;

(3.37)

ЛАЧХ: L( )= 20 lg k + 10 lg(1+T) .

(3.38)

Рис.3.19. ЛАЧХ форсирующего звена

Асимптотическую ЛАЧХ форсирующего звена можно получить, рассматривая отдельно области низких и высоких частот, как в случае апериодического звена, или суммируя ЛАЧХ пропорционального и дифференцирующего звеньев.

Рис.3.20 АФХ форсирующего звена

Здесь - собственная частота звена. АФХ форсирующего звена строится по выражению (3.36) и имеет вид, представленный на рис. 3.20.

3.7. Звено второго порядка

Дифференциальное уравнение звена второго порядка

,

(3.39)

где a₂, a₀, b 0, принято записывать в стандартном виде:

,

(3.40)

где , d - коэффициент демпфирования, который определяет склонность звена к колебаниям, , - коэффициент передачи.

Передаточную функцию получим на основе символической записи дифференциального уравнения,

y + 2d py + y = ku,

в виде:

.

(3.41)

Определим модальные характеристики по характеристическому уравнению

.

(3.42)

Оно имеет два корня, которые в зависимости от коэффициента демпфирования могут быть вещественными и комплексно - сопряженными, что приводит к различным переходным процессам в звене.

Рис.3.21. Переходная характеристика звена 2-го порядка при

1). Если , то корни уравнения (3.42) вещественные. Обозначим их через и получим переходную функцию в виде: . (3.43)

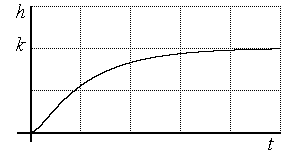
Рис.3.22. Переходная характеристика звена при , Т > 0

2). Если , то корни уравнения (3.42) будут комплексно - сопряженными, то есть (а при d = 0 получаем ).

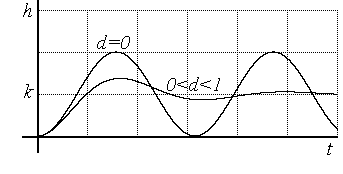
Если , то звено второго порядка называют колебательным. Его переходная функция следующая:

.

(3.44)

Колебательность переходного процесса зависит от коэффициента демпфирования d: она будет тем больше, чем меньше d. При d = 0 имеют место незатухающие колебания.

Определим частотные характеристики звена, заменив p на j в передаточной функции (3.41).

.

(3.45)

Отсюда получим выражения для ВЧХ и МЧХ в виде:

,

(3.46)

.

(3.47)

При построении АФХ на комплексной плоскости необходимо рассматривать характерные точки:

Рис.3.23. АФХ звена второго порядка

Вид АФХ существенно зависит от k и d. При d=0 АФХ совпадает с вещественной осью.

На основе выражения

.

(3.48)

строится ЛАЧХ.

Асимптотическую ЛАЧХ колебательного звена (при ) также можно построить, если рассматривать отдельно области высоких и низких частот и для каждой определить свою асимптоту:

ОНЧ: , L( )= L1( )=20 lg k.

(3.49)

ОВЧ: , L ( )=L2( ) = 20 lgk -40lg( ).

(3.50)

Частота называется собственной частотой колебательного звена. Причем на этой частоте для асимптотической ЛАЧХ справедливо соотношение: .

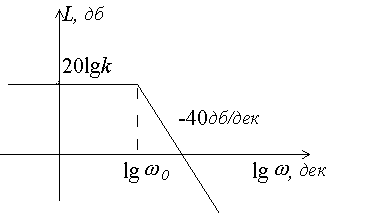
Рис.3.24. Асимптотическая ЛАЧХ колебательного звена

Наибольшее отличие асимптотической ЛАЧХ от действительной наблюдается на собственной частоте и зависит от коэффициента демпфирования.

При с достаточной точностью можно применять асимптотическую ЛАЧХ звена.

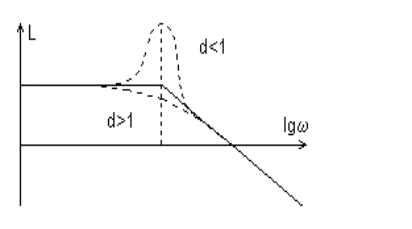
Рис.3.25. Влияние d на ЛАЧХ звена

Если d < 0,5, то следует строить точную ЛАЧХ. При d > 1 корни характеристического уравнения (3.42) будут вещественными, и передаточную функцию звена второго порядка (3.41) можно представить в виде

произведения двух передаточных функций апериодических звеньев:

,

(3.51)

где - постоянные времени апериодических звеньев. В этом случае асимптотическая ЛАЧХ звена второго порядка имеет два излома на частотах . Она может быть получена суммированием асимптотических ЛАЧХ двух апериодических звеньев.
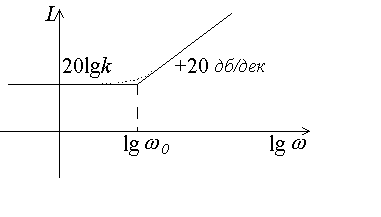
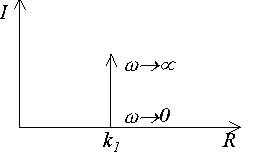
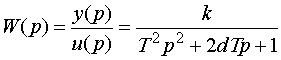
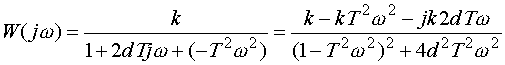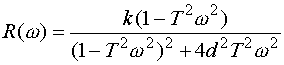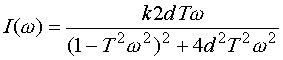
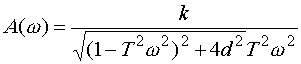
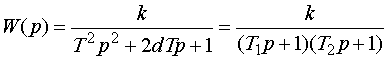