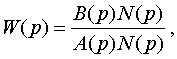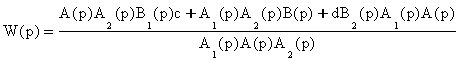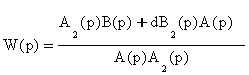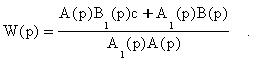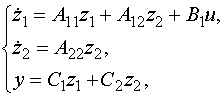6.3.2. Устойчивость “обратного” объекта

Это условие также связано со свойствами объекта. Для его получения представим структурно выражение для управляющего воздействия (6.9), позволяющее точно обеспечить в замкнутой системе желаемую передаточную функцию. Как видим (рис.6.4), управление является выходом обратной модели объекта.

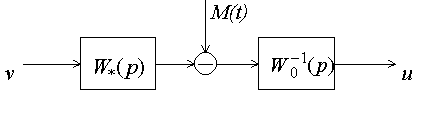
Рис.6.4. Cтруктурная интерпретация управления

Отсюда следует второе условие разрешимости: обратная модель объекта (p ) должна быть устойчивой, то есть необходимо, чтобы корни полинома B(p) располагались в левой полуплоскости плоскости корней:

Re {B( p) = 0} < 0 .

(6.11)

Пример 6.1.

Покажем проявление этого условия для следующей системы:

Рис.6.5. Структурная схема системы

Здесь k - коэффициент усиления регулятора; - передаточная функция объекта управления.

Характеристическое уравнение системы имеет вид

A(p)+ k B(p) = 0 .

Для уменьшения статической ошибки увеличивают общий коэффициент усиления. В пределе при характеристическое уравнение вырождается в следующее:

Таким образом, условие (6.11) - это реальное условие устойчивости замкнутой системы.

6.3.3. Вырожденность передаточной функции

При получении передаточных функций реальных систем в числителе и знаменателе могут появиться одинаковые или близкие сомножители, например,

(6.12)

после сокращения которых получают вырожденную передаточную функцию

Система будет работоспособной только в том случае, когда выполняется условие разрешимости: общие сомножители числителя и знаменателя имеют корни с отрицательной вещественной частью,

Re {N(p) = 0} < 0.

(6.13)

Пример 6.2.

Покажем, к чему приведет несоблюдение этого условия для объекта, который состоит из трех параллельных каналов.

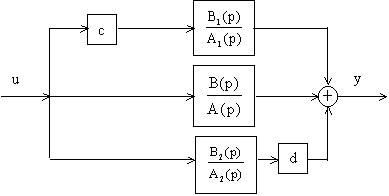
Рис.6.6. Структурная интерпретация условия разрешимости

Определим для него передаточную функцию,

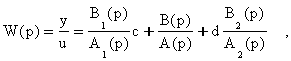< span>

которую представим в виде

(6.14)

Если здесь теперь полагать c = 0, то получим передаточную функцию,

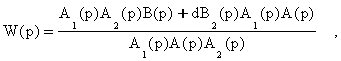
которая при выполнении условия типа (6.13): Re { (p) = 0} < 0,принимает вид:

(6.15)

Наличие сокращаемого множителя в числителе и знаменателе функции (6.14) структурно означает появление неуправляемой части: при c = 0 происходит разрыв связи, и управление не действует на звено с передаточной функцией 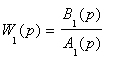, процессы в котором развиваются в силу собственных свойств.

При d = 0 вместо (6.14) имеем

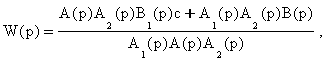
или при выполнении условия: Re { (p) = 0} < 0,

(6.16)

Это соответствует наличию ненаблюдаемой части системы с передаточной функцией 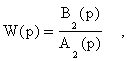которая не оказывает влияния на выход системы.

При неустойчивой неуправляемой или ненаблюдаемой части объекта замкнутая система окажется неработоспособной.

6.3.4. Управляемость

Понятия управляемости и наблюдаемости имеют большое значения для линейных многоканальных систем.

Рассмотрим условие управляемости для объектов вида

(6.17)

Объект (6.17) называется управляемым, если существует ограниченное управляющее воздействие u(t), которое переводит его из начального состояния x (0) в заданное конечное x(T) за конечное время T.

Проверяется это условие с помощью критерия управляемости. Объект (6.17) управляем тогда и только тогда, когда матрица управляемости

(6.18)

имеет полный ранг.

Так как матрица U имеет n строк и ( ) столбцов, то критерий управляемости записывается в виде

r { U } = n .

(6.19)

Определить, имеет ли матрица полный ранг, можно по соотношению:

det { U } 0 .

(6.20)

Для одноканального объекта, когда m= 1, критерий управляемости (6.19) принимает форму

det { U } 0 .

(6.21)

В случае неуправляемого объекта с помощью невырожденного преобразования переменных,

z = M x , det M 0 ,

переходят к канонической форме управляемости (рис.6.7).

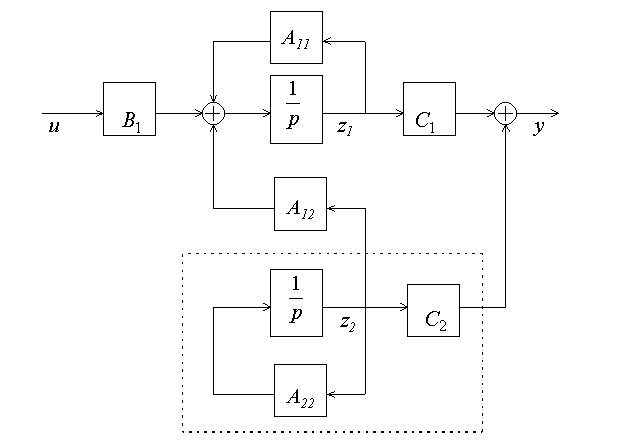
Рис.6.7. Cтруктурная схема неуправляемого объекта

Уравнения объекта, записанные в канонической форме, имеют вид:

(6.22)

где переменные характеризуют автономную часть объекта, называемую неуправляемой. Однако эта часть влияет на выходные переменные, что хорошо иллюстрирует схема, приведенная на рис.6.7.

Поскольку процессы в неуправляемой части развиваются в силу собственных свойств и изменить их невозможно, то в случае ее неустойчивости весь объект будет не только неустойчивым но и нестабилизируемым.