6.5.2. Постановка задачи синтеза для одноканального объекта
Рассматривается объект управления, передаточная функция которого имеет вид:
|
(6.47) |
где m
n.
Влияние окружающей среды отражает
возмущение M(t).
Модальный метод синтеза предполагает формирование заданной реакции системы на отработку начальных условий, которая определяется корнями характеристического уравнения. Если они выбраны на основе требований, предъявляемых к динамике в виде условий (6.4) и (6.5), то соответствующее характеристическое уравнение называют желаемым.
Таким образом, задача синтеза заключается в обеспечении в замкнутой системе желаемого характеристического уравнения.
Для ее решения
предлагается использовать в качестве
регулятора последовательное звено
и
звено с передаточной функцией
в
обратной
связи,
то есть структура системы задана и имеет
вид, приведенный на рис.6.14.
Звено прямого канала с передаточной функцией будем называть корректором статики, а звено с передаточной функцией - корректором динамики. При синтезе структура их известна, требуется определить параметры.
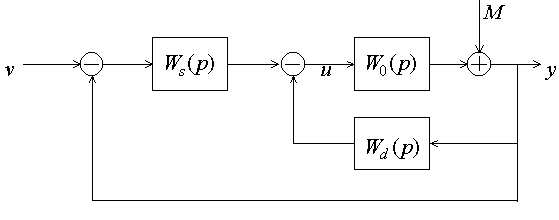
Рис.6.14. Расчетная структурная схема замкнутой системы
Рассмотрим последовательно этапы модального метода синтеза.
6.5.3. Обеспечение заданной статики
С целью выполнения
условия статики (6.4),
,
при произвольном возмущении
M
предлагается в качестве звена с
передаточной функцией
использовать
интегратор,
|
(6.48) |
,
то есть сделать
систему астатической.
Здесь
-
неизвестный пока коэффициент передачи
регулятора.
Полагая, что объект и корректор динамики не содержат интегрирующих звеньев, запишем операторное выражение для выходной величины
|
(6.49) |
.Отсюда в статике, при p =0,когда передаточные функции вырождаются в коэффициенты усиления, получим y (p)= v.
Как видим, с помощью
выбранного корректора статики
можно
обеспечить выполнение условия (6.4)
с ошибкой
.
6.5.4. Расчет корректора динамики
Рассмотрим теперь характеристическое уравнение системы, приведенной на рис.6.14:
|
(6.50) |
.В качестве корректора динамики предлагается выбирать следующую передаточную функцию:
|
(6.51) |
,
где B(p)
- полином числителя
,
а D(p)
- введенный расчетный полином с
неизвестными коэффициентами d
i
,
.
С учетом (6.51) характеристическое уравнение (6.50) замкнутой системы принимает вид:
pA(p) + pD(p) + B(p) = 0, |
(6.52) |
причем его порядок равен (n+1).
Подставляя вместо A(p), D(p) и B(p) их значения, получим
.
На основе требований
к качеству переходных процессов
(заданного перерегулирования
и
быстродействия
)
сформируем желаемое характеристическое
уравнение того же порядка, что и (6.52):
|
(6.53) |
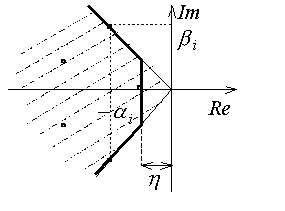
.Для конструирования C(p) используем корневые оценки переходных процессов, с помощью которых получим эталонное распределение корней на комплексной плоскости.
Риc.6.15. Желаемое расположение корней |
Так расстояние, ближе которого не могут располагаться корни уравнения (6.53), зависит от и приближенно может быть найдено по соотношению:
Сектор, внутри которого находятся корни, определяется на основе зависящего от значения колебательности *. |
Вычисляется значение мнимой части корней с “максимальным” размахом:
|
(6.55) |
.
Эталонные корни
выбираются
внутри ограниченной области (рис.6.15),затем
следующим образом формируется желаемое
уравнение (6.53):
|
(6.56) |
.Приравнивая коэффициенты при соответствующих степенях желаемого (6.53) и действительного (6.52) характеристических уравнений, получим (n+1) расчетное соотношение для определения неизвестных коэффициентов регулятора,
|
(6.57) |
.Они легко вычисляются из (6.57) и имеют вид:
|
(6.58) |
Таким образом, мы определили параметры передаточных функций регулятора, обеспечивающего в системе требуемые свойства. Рассмотрим теперь возможности его реализации.
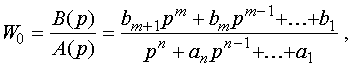
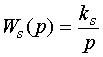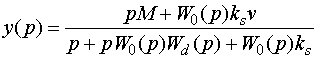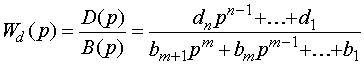
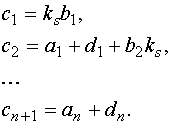