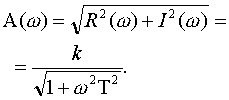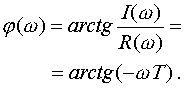3.3. Дифференцирующее звено
Дифференцирующим называется звено, которое описывается дифференциальным уравнением:
y = k
|
(3.6) |
.Его передаточная функция имеет вид:
W(p) = y(p)/u(p) = kp. |
(3.7) |
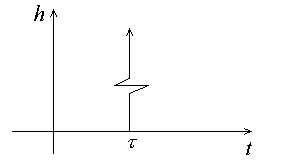
Рис.3.5. Переходная характеристика звена |
Переходная характеристика дифференцирующего звена: h(t)
= k |
(t-
).
Рис.3.6. Импульсная характеристика |
Импульсная функция имеет вид
|
(t-
).Получим теперь частотные характеристики звена.
АФХ
: W(j
)
= j k
,
совпадает с положительной мнимой
полуосью на комплексной плоскости;
ВЧХ : R( ) = 0 ,
МЧХ : I( ) = k ,
АЧХ
:
,
ФЧХ
:
,то
есть для всех частот звено вносит
постоянный фазовый сдвиг;
Рис.3.7. ЛАЧХ дифференцирующего звена |
ЛАЧХ :
Как видно из графика рис.3.7, дифференцирующее звено усиливает высокочастотные сигналы. |
)=20lg(k
)=
20lg(k)+20lg(
).
3.4. Интегрирующее звено
Это звено, уравнение которого имеет вид:
|
(3.10) |
.От интегрального перейдем к дифференциальному уравнению звена
|
(3.11) |
,а затем к его передаточной функции
|
(3.12) |
.Переходная характеристика звена имеет вид:
|
(3.13) |
,а импульсная функция -
|
(3.14) |
.Определим частотные характеристики интегрирующего звена.
|
АФХ:
ВЧХ:
МЧХ:
ФЧХ
:
|
;
;
;
;
.
Звено имеет постоянный фазовый сдвиг, который не зависит от частоты.
АФХ интегрирующего звена изображается на комплексной плоскости и имеет вид, представленный на рис.3.8.
Рис.3.9. ЛАЧХ интегрирующего звена |
Получим логарифмическую амплитудно-частотную характеристику:
она имеет вид прямой на плоскости (рис.3.9). |
Характеристическое уравнение
A(p) = p = 0
имеет единственный
корень,
,
который представляет собой модальную
характеристику интегрирующего звена.
3.5. Апериодическое звено
Апериодическим называется звено, дифференциальное уравнение которого имеет вид
|
(3.17) |
.Перейдем к его стандартному описанию, для чего разделим обе части (3.17) на коэффициент a0 ,
|
(3.18) |
,
где
,
-
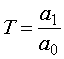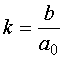коэффициент передачи звена.
Заменив в (3.18) d/dt на p, перейдем к символической записи дифференциального уравнения,
(Tp+1)y = ku, |
(3.19) |
и определим передаточную функцию апериодического звена:
|
(3.20) |
.
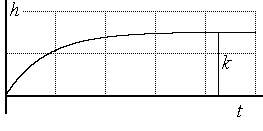
Рис.3.10. Переходная характеристика |
Его переходную характеристику можно найти как решение уравнения (3.18) при u=1(t) и y(0)=0,
|
)·1(t).
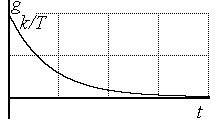
Рис.3.11. Импульсная функция |
Импульсную функцию вычислим по соотношению:
|
(t)=
·1(t).Для определения модальных характеристик запишем характеристическое уравнение звена
A(p) = Тр + 1 = 0 |
(3.23) |
и вычислим его корень р = -1/Т .
Выражение, соответствующее АФХ апериодического звена имеет вид:
|
(3.24) |
.
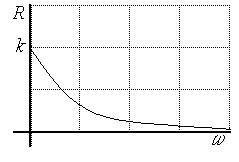
Рис.3.12. ВЧХ звена |
Построим отдельно вещественную частотную характеристику по выражению
|
.
Рис.3.13. МЧХ звена |
Мнимую частотную характеристику апериодического звена строим по соотношению
|
.
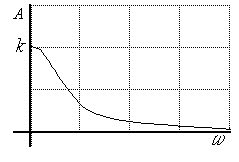
Рис.3.14. АЧХ апериодического звена |
Построим амплитудную частотную характеристику по выражению:
|
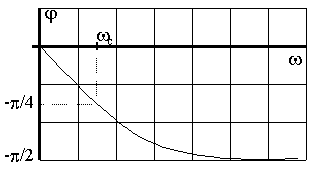
Рис.3.15. ФЧХ апериодического звена |
ФЧХ звена определяется соотношением
|
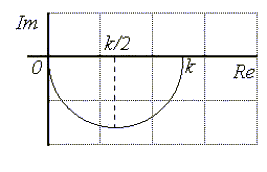
Рис.3.16 АФХ апериодического звена. |
На комплексной плоскости строим АФХ апериодического звена по выражению (3.24), которая имеет вид полуокружности и приведена на рис.3.16. Определим теперь логарифмическую амплитудную частотную характеристику в виде: |
|
(3.29) |
.Наиболее просто можно построить асимптотическую ЛАЧХ. В этом случае рассматривают отдельно области высоких (ОВЧ) и низких частот (ОНЧ) и для каждой определяют свою асимптоту:
1) ОНЧ: <<1/T, L( )=20lg(k). |
(3.30) |
2) ОВЧ: >>1/T, L( )=20lg(k)-20lg(T ). |
(3.31) |
Частота
1/T
называется
собственной
частотой апериодического звена.
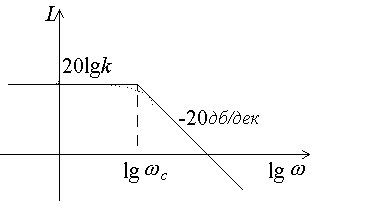
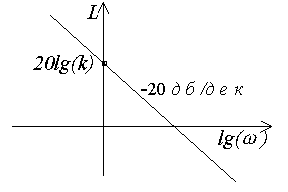
Рис.3.17. ЛАЧХ апериодического звена |
На рис.3.17 действительная ЛАЧХ показана пунктирной линией и несколько отличается от асимптотической, причем наибольшая погрешность будет на собственной частоте звена. |
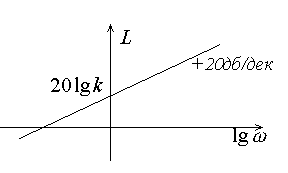
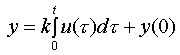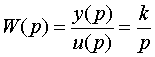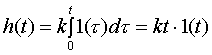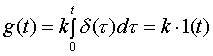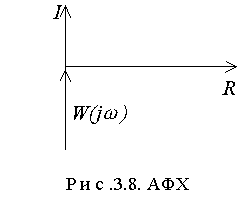
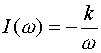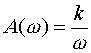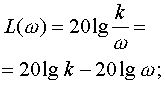
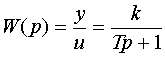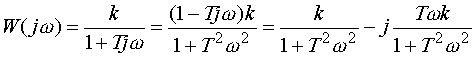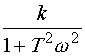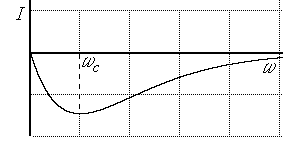
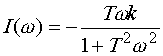