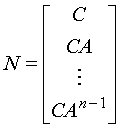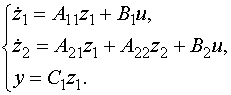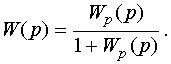6.3.5. Наблюдаемость
Это понятие отражает возможность оценки переменных состояния объекта (6.17) по результатам измерения физических переменных.
Объект называется наблюдаемым, если в любой момент времени можно оценить его состояние x по данным измерения выходных переменных y(t) и управляющих воздействий u(t).
Условие проверяется с помощью критерия наблюдаемости. Объект (6.17) наблюдаем тогда и только тогда, когда матрица наблюдаемости
|
(6.23) |
имеет полный ранг, то есть
rank(N)=n |
(6.24) |
Это условие можно проверить по соотношению:
det {
N
}
0
.
В случае одноканального объекта критерий наблюдаемости (6.24) принимает вид
det { N } 0 . |
(6.25) |
Для ненаблюдаемого объекта существует невырожденная матрица преобразования M,
z = M x ,det M 0,
которая позволяет уравнения (6.17) записать в канонической форме наблюдаемости
|
(6.26) |
Здесь переменные характеризуют ненаблюдаемую часть объекта, структурная схема которого приведена на рис.6.8.
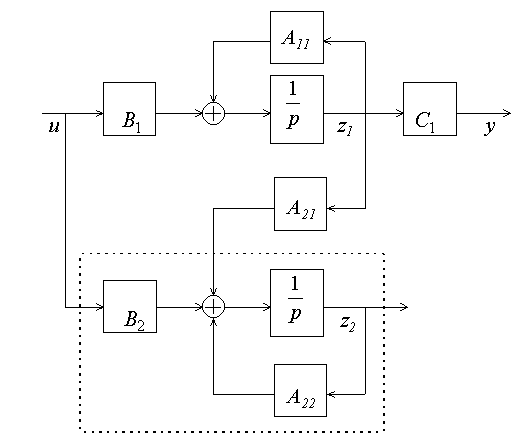
Рис.6.8. Структурная схема ненаблюдаемого объекта
Если ненаблюдаемая часть неустойчива, то с объектом работать нельзя.
Таким образом, условие разрешимости задачи синтеза - устойчивость ненаблюдаемой части объекта.
6.4.1. Постановка задачи
Рассматривается объект управления, поведение которого описывается передаточной функцией ( p), а выходная переменная измеряется с помехой h(t). Влияние окружающей среды отражает возмущение M(t).
Требования к поведению системы задаются
в виде оценок переходного процесса, в
качестве которых используются статическая
ошибка (
),
перерегулирование
и быстродействие
(
%
и
).
Необходимо определить передаточную
функцию корректирующего звена (регулятора)
(
p),
включение которой в систему обеспечит
заданное качество работы.
Метод предназначен для синтеза одноканальных систем, работающих в режиме слежения или отработки входа (стабилизации), и предполагает использование асимптотических ЛАЧХ. При этом расчетная структурная схема имеет вид:
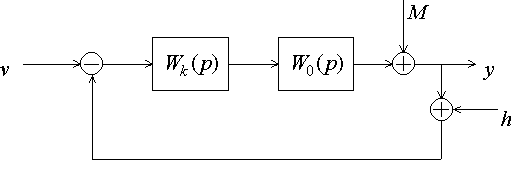
Рис.6.9. Структурная схема замкнутой системы
Первоначально будем рассматривать реакцию только на входное воздействие, полагая возмущение и помеху равными нулю (M =0,h=0). Их влияние на свойства системы учтем в дальнейшем.
Вычислим передаточную функцию разомкнутой системы,
|
(6.27) |
,а затем замкнутой:
|
(6.28) |
Как видим, ее однозначно определяет
(p).
Следовательно, если удастся сформировать заданную передаточную функцию или частотную характеристику разомкнутой системы, то тем самым можно обеспечить требуемые свойства для замкнутой системы.
6.4.2. Влияние частотной характеристики разомкнутой системы на свойства замкнутой
От передаточной
функции
разомкнутой системы
(6.27)
перейдем к ее частотной
характеристике
заменой
,
|
(6.29) |
которую рассмотрим подробнее в различных областях частот, введя предварительно несколько определений.
Зоной низких
частот
будем называть область изменения
.
В ней по условию статики выполняется
соотношение:
где
-
коэффициент усиления объекта. Для
разомкнутой системы в соответствии с
(6.29) получим
|
(6.30) |
Областью высоких частот будем называть совокупность частот . Здесь справедливы соотношения:
|
(6.31) |
Зона средних частот - это область изменения , где выполняются соотношения:
|
(6.32) |
Поскольку частотные характеристики разомкнутой и замкнутой системы связаны соотношением, аналогичным (6.28), то с учетом (6.30) в области низких частот (НЧ) получим
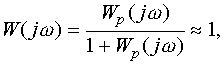
то есть вид частотной характеристики разомкнутой системы мало влияет на систему в целом.
В области высоких частот (ВЧ) с учетом (6.31) имеем
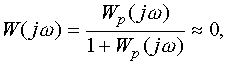
а значит вид частотной характеристики разомкнутой системы не влияет на свойства замкнутой.
Таким образом,
наибольшее влияние
оказывает
на свойства замкнутой системы в области
средних частот (СЧ),
где наиболее тщательно следует выбирать
желаемую характеристику.