
- •1. Введение Основные понятия и определения
- •2. Динамические характеристики линейных систем
- •2.1. Дифференциальные уравнения
- •2.2. Составление математической модели
- •2.3. Структурные схемы
- •2.4. Переходная функция (переходная характеристика)
- •2.6. Переходная матрица
- •2.7. Передаточная функция
- •2.8. Модальные характеристики
- •2.9. Частотные характеристики
- •3. Структурный метод
- •3.1. Введение
- •3.1. Введение
- •3.2. Пропорциональное звено (усилительное, безынерционное)
- •3.3. Дифференцирующее звено
- •3.4. Интегрирующее звено
- •3.5. Апериодическое звено
- •3.6. Форсирующее звено (пропорционально - дифференцирующее)
- •3.7. Звено второго порядка
- •3.8.1. Последовательное соединение звеньев
- •3.8.2. Параллельное соединение звеньев
- •3.8.3. Обратная связь
- •3.8.4. Правило переноса
- •3.9. Переход от передаточных функций к уравнениям состояния с использованием структурных схем
- •3.10. Область применимости структурного метода
- •4. Устойчивость линейных непрерывных систем
- •4.1. Основные понятия и определения
- •4.2. Условие устойчивости линейных систем
- •4.3. Критерии устойчивости
- •4.3.1. Критерий устойчивости Гурвица
- •4.3.2. Критерий устойчивости Михайлова
- •Доказательство
- •4.3.3. Критерий устойчивости Найквиста
- •4.3.4. Логарифмическая форма критерия Найквиста
- •4.4.1.Основные понятия и определения
- •4.4.2. Частотные оценки запаса
- •4.4.3. Корневые оценки
- •4.4.4. Метод d-разбиения
- •5. Анализ переходных процессов
- •5.2. Показатели качества переходного процесса
- •5.2.1. Ошибка регулирования
- •5.2.2. Быстродействие
- •5.2.3. Перерегулирование
- •5.2.4. Интегральные оценки
- •5.3. Анализ статических режимов
- •5.3.1. Статические системы
- •5.3.2. Астатические системы
- •5.3.3. Следящие (позиционные) системы
- •5.4.1. Введение
- •5.4.2. Взаимосвязь между частотной характеристикой и импульсной функцией
- •5.4.3. Взаимосвязь между частотной и переходной характеристиками
- •5.4.4. Оценки качества переходного процесса по вещественной частотной характеристике
- •5.4.5. О начальном участке переходной характеристики
- •5.5.1. Введение
- •5.5.2. Корневые оценки переходного процесса
- •5.6.1. Система 1-го порядка
- •5.6.2. Система 2-го порядка
- •5.6.3. Система 3-го порядка
- •6. Синтез линейных систем
- •6.1. Основные понятия
- •6.2. Постановка задачи синтеза одноканальных систем
- •6.3. Условия разрешимости задачи синтеза
- •6.3.1. Ресурсное ограничение
- •6.3.2. Устойчивость “обратного” объекта
- •6.3.3. Вырожденность передаточной функции
- •6.3.4. Управляемость
- •6.3.5. Наблюдаемость
- •6.4.1. Постановка задачи
- •6.4.2. Влияние частотной характеристики разомкнутой системы на свойства замкнутой
- •6.4.3. Основные соотношения и методика расчета
- •6.4.4. Построение лачх объекта
- •6.4.5. Построение желаемой лачх
- •6.4.6. Расчет корректирующего звена
- •6.4.7. Влияние возмущения и помехи измерения на свойства замкнутой системы
- •6.5.1. Основные понятия
- •6.5.2. Постановка задачи синтеза для одноканального объекта
- •6.5.3. Обеспечение заданной статики
- •6.5.4. Расчет корректора динамики
- •6.5.5. Схема реализации регулятора
5.2.1. Ошибка регулирования
Для оценки точности используется величина ошибки
|
(5.4) |
которая с течением времени стремится к некоторому постоянному значению, называемому статической ошибкой:
|
(5.5) |
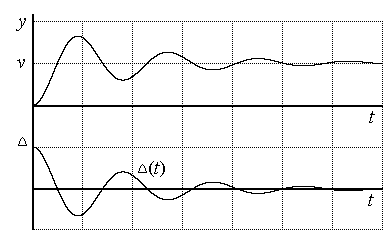
Рис.5.2. Изменение ошибки во времени |
При известной структурной схеме системы ошибку можно определить в операторной форме с помощью структурных преобразований,
|
В этом случае статический режим характеризуется тем, что p=0, а статическая ошибка находится по выражению
|
(5.7) |
Динамической ошибкой будем называть величину
|
(5.8) |
причем
![]()
Ошибка (статическая ошибка) является одной из основных количественных характеристик динамики системы.
5.2.2. Быстродействие
Быстродействие – это оценка скорости реагирования системы регулирования на появление задающих и возмущающих воздействий.
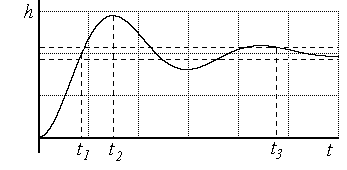
В качестве оценок быстродействия можно использовать различные величины, причем все они определяют время от начала процесса до какого-либо характерного значения. С этой целью рассмотрим переходную характеристику системы h(t).
Рис.5.3. Иллюстрация оценок быстродействия |
Оценками быстродействия могут служить:
|
![]() -
время достижения первого максимума
(также возможно только для колебательных
процессов);
-
время достижения первого максимума
(также возможно только для колебательных
процессов);
![]() -
время от начала процесса до момента
достижения установившегося значения
не
более заданной.
-
время от начала процесса до момента
достижения установившегося значения
не
более заданной.
На практике в
качестве оценки быстродействия чаще
всего используют величину
,
которую обычно обозначают как
![]() и
называют временем
переходного процесса.
и
называют временем
переходного процесса.
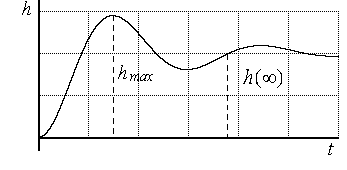
5.2.3. Перерегулирование
Эта количественная
оценка характеризует колебательные
свойства системы,
обозначается буквой
![]() и
определяется в процентах относительно
установившегося значения по выражению
и
определяется в процентах относительно
установившегося значения по выражению
|
(5.9) |
Риc.5.4. Иллюстрация оценки перерегулирования |
Чем больше
перерегулирование
|
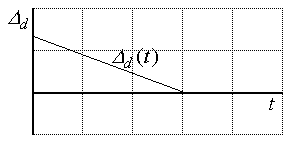
5.2.4. Интегральные оценки
Интегральные оценки представляют собой обобщенные показатели качества переходного процесса. Обычно для их определения используют динамическую ошибку.
Риc.5.5. Динамическая ошибка системы |
В качестве интегральной оценки можно использовать следующие величины:
которая дает надежные результаты только в случае монотонного переходного процесса. |
2) |
|
(5.11) |
характеризует
площадь под кривой
![]() на
рис.5.5.
на
рис.5.5.
3) |
|
(5.12) |
Наиболее удобной
из приведенных является интегральная
оценка
![]() ,
которая сравнительно просто вычисляется
и применяется как для монотонного, так
и для колебательного процесса. Она
характеризует также затраты энергии
на совершение переходного процесса.
,
которая сравнительно просто вычисляется
и применяется как для монотонного, так
и для колебательного процесса. Она
характеризует также затраты энергии
на совершение переходного процесса.
Риc.5.6. Идеальный переходный процесс |
Идеальный переходный процесс (без лишних потерь энергии) представлен на рис.5.6. В общем виде интегральная оценка качества переходного процесса записывается следующим образом: |
|
(5.13) |
Применение конкретной интегральной оценки зависит от вида переходного процесса и требований, предъявляемых к системе.

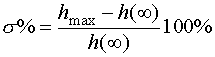 .
.
 <
p>
<
p>
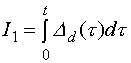 ,
,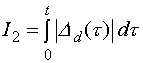
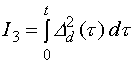 .
.
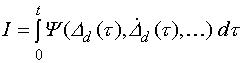 .
.