4.3.2. Закон Біо–Савара–Лапласа

Напруженість магнітного поля Н, створеного постійним струмом, можна обчислити, використовуючи закон, відкри­тий експериментально французькими фізиками Ж.Б. Біо і Ф. Саваром у 1820 р. і сформульований в загальному вигляді П.С. Лапласом.

В

Мал. 4.17.

иділимо в провіднику зі струмом достатньо малу ділян­ку dl, яку можна розглядати як вектор, направлений в той же бік, що й струм I. Добуток Idl називають елементом струму. Проведемо з елемента струму Idl радіус-вектор r в досліджувану точку A (мал. 4.17). Тоді величина напруженості магнітного поля в точці A, створеного даним елементом струму, дорівнює:

dH = , (4.45)

де  – кут між векторами dl і r, коефіцієнт k залежить від вибору системи одиниць. В системі СІ: k = 1/4. Напрямок dН визначається правилом свердлика: якщо поступальний рух свердлика збігається з напрямком dl, то напрямок dH збігається з напрямком обертання рукоятки. Повна напруженість H магнітного поля, створеного в точці A провідни­ком зі струмом, дорівнює векторній сумі полів, створе­них всіма елементами струму Idl, що складають даний провід­ник. Якщо всі dH мають однаковий напрямок, то сумарна напруженість маг­нітно­го поля знаходиться як інтеграл:

H = . (4.46)

З

Мал. 4.18.

найдемо напруженість магнітного поля у вакуумі для деяких простих контурів зі струмом.

Напруженість магнітного поля в центрі колового струму. Коловим називають струм, що протікає по про­від­нику у формі кола (мал. 4.18). У цьому випадку всі елементи dl про­від­ника перпендикулярні до радіус-вектора: sin = 1. Відстань від усіх елементів провідника до центра кола однакова і дорівнює радіусу кола R, . Тому інтегру­ван­­ня в (4.46) дає:

H = = = . (4.47)

Напрямок вектора Н можна знайти за правилом свердлика і він буде таким, як показано на мал. 4.18 (вектор Н перпен­ди­кулярний до площини провідника).

Магнітне поле прямолінійного провідника зі струмом (мал. 4.19) обчислюється за формулою:

H = ,

д

Мал. 4.19.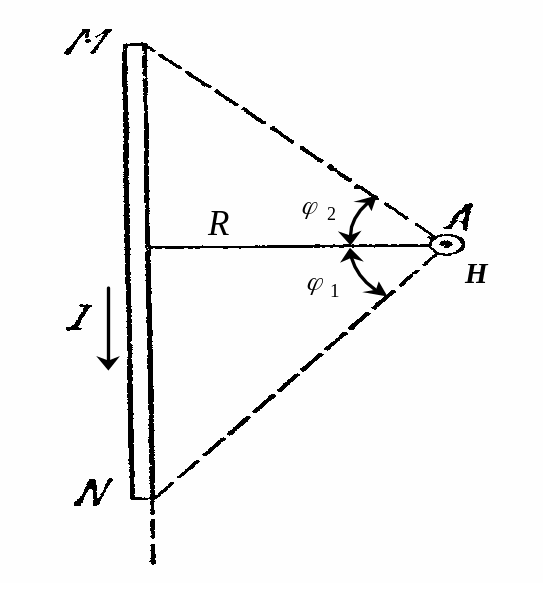

е R – відстань від провідника зі стру­мом до даної точки, I – сила струму в про­віднику.

Якщо провідник нескінченно дов­гий, то ₁  –/2, а ₂  /2, і

H = . (4.48)

Магнітне поле на осі соленоїда визначається за формулою:

H = nI, (4.49)

де n – число витків, які припадають на одини­цю довжини cоленоїда. Величи­на поля на осі не залежить від радіуса соленоїда R, якщо його довжина L >> R.

4.3.3. Дія магнітного поля на рухомий електричний заряд. Сила Ампера і сила Лоренца

Силова дія магнітного поля на провідник зі струмом визначається відповідно до емпіричного закону Ампера (1820 р.):

F_А = IBdlsin, (4.50)

де  – кут, утворений векторами dl і B. Сила Ампера F_A діє на провідник зі струмом в магнітному полі. Вона є результатом дії магнітного поля на рухомі електричні заряди, котрі створюють даний електричний струм I. Сила f_л, яка діє на окремий рухомий заряд, називається силою Лоренца і може бути визначена із співвідно­шення:

,

де N = nV = ndlS – загальна кількість вільних носіїв заряду в провіднику. Враховуючи, що I = jS, а j = q₀nυ, отримаємо вираз для сили Лоренца, що діє з боку магнітного поля на окремий електричний заряд q₀, який рухається зі швид­кіс­­тю υ:

f_л = q₀υBsin, (4.51)

де  – кут між векторами υ і B. Напрям сили Лоренца визначається, як і напрям сили Ампера, за правилом свердлика i залежить від знаку заряда (мал. 4.20). Оскільки сила Лоренца перпендикулярна до площини, в якій лежать вектори υ і B, то ця сила надає частинці доцентрового прискорення. Припустимо, що заряджена частинка q₀ влітає з швидкістю υ в однорідне магнітне поле B перпендикулярно до силових ліній, тоді відповідно до другого закону Нью­тона

mυ²/R = q₀υB. (4.52)

Звідси – радіус кола, по якому рухається частинка.

Період обертання

T = = . (4.53)

Мал. 4.20.

Період обертання не залежить від швидкості (справедливe для швидкостей υ < c), але залежить від величини магнітної індукції В та питомого заряду частинки q₀/m. Ця особливість має широке практичне використання. У багатьох системах (осцилограф, телевізор, електронний мікро­скоп, прискорювач) управління електронами чи іншими зарядженими частинками здійснюють, діючи на них електричними і магнітними полями. Результуюча сила в цьому випадку дорівнює

F = F_e + F_м = qE + q[υB], (4.54)

де [υB] – так званий векторний добуток υ та B. Це вектор, модуль якого дорів­нює υBsin, де  – кут між цими векто­ра­ми, а напрям визначаєть­ся за правилом свердлика.

Cила Лоренца є причиною виникнення ефекту Холла. Ефектом Холла називають появу поперечної різниці потенціалів, що виникає у провіднику зі струмом, внесеному у магнітне поле, вектор індукції якого перпендикулярний до напрямку струму. Розглянемо деякі застосування описаних вище явищ.

Мас-спектрографія. Для визначення питомого заряду і маси іонів використовують сумісну дію електричного і маг­ніт­ного полів. Прилади, призначені для точних вимірю­вань питомих зарядів (а значить, і мас) ізотопів хімічних елементів, а також їхнього вмісту в складних речовинах, називають мас-спектрографами і мас-спектро­метрами. Атоми чи молекули досліджуваної речовини попередньо іонізуються, а потім за допомогою електричного та магнітного полів сор­тують­ся та реєструються окремо залежно від їхнього питомого заряду q/m. Це є дуже важливим, зокрема, для визначення молекулярних механізмів хімічних і біологічних реакцій.

Електромагнітні вимірювачі швидкості крові. Для ви­мі­рю­­ван­ня швидкості крові в судинах системи кровообігу розроблено чимало методів. Один із них базується на дії магнітного поля на рухомі заряди. Кров містить значну кількість електричних зарядів: концентрація іонів Na⁺  145 ммоль/л, Сl^–  125 ммоль/л.

Якщо артерію діаметром d помістити між полюсами маг­ніту, то на одновалентні іони діятиме сила Лоренца f_л = = eB. Під її впливом іони різних знаків рухатимуться до протилежних стінок артерії і ство­рять вздовж вертикалі різницю потенціалів U, тобто електричне поле з напруженістю Е = U/d (ефект Холла). Концентрація зарядів на протилежних стінках артерії зростатиме, поки сила F_ел = eE, ство­рюваного ними поля, не компенсує силу Лоренца. З рівності F_л = F_ел можна знайти швидкість руху іонів, а значить і крові:

. (4.55)

Отже, швидкість руху крові пропорційна напрузі (різ­ниці потенціалів при ефекті Холла), яка виникає впоперек артерії, якщо внести її в магнітне поле.