4.4.3. Повний опір кола змінного струму (імпеданс). Закон Ома для кола змінного струму

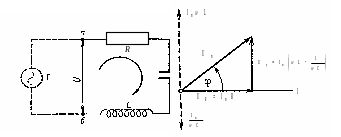
Отримані результати дозволяють знайти співвідно­шен­ня між коливаннями сили струму та напруги в будь-якому колі. Розглянемо спочатку коло, в яке послідовно ввімкнені активний опір R, ємність С та індуктивність L (мал. 4.35). Сила струму в загальному випадку відрізняється за фазою від напруги U і є однаковою для кожного елемента кола: I = I_msin t.

Оскільки при послідовному з’єднанні додаються напру­ги, то шу­кану напругу можна подати як суму спадів напруг на окремих ділян­ках: U = U_R + U_L + U_C. Для додавання цих трьох гармонічних коливань скористаємося векторною ді­агра­мою. Врахуємо, що напру­га на омічному опорі синфазна з силою струму, напруга на індук­тив­нос­­ті випереджає силу струму на /2, а на ємності ж відстає на /2 (мал. 4.36). Додаючи два останні коливання U_L і U_C, ми отримаємо од­не гармо­нічне коливання, яке зображується вектором U_p, перпенди­­ку­лярним до осі струмів; довжина цього вектора U_p = = І_m(L – 1/C). Цей спад напруги називається реактивною складовою спаду напруги, а відповідний опір (L – 1/C) – реактивним опором. Таким чином, повний спад напруги U_m можна розглядати як суму двох гармонічних коливань: активної складової І_mR та реактивної U_р, які відрізняються за фазою на /2. Величину U_m можна знайти за теоремою Піфагора (мал. 4.36):

U_m² = (I_mR)² + (I_mL – I_m /C)². (4.76)

Мал. 4.35.

Мал. 4.36.

Для макимального значення повного спаду напруги в контурі закон Ома має вигляд

U_m = I_mZ,

де Z – повний опір кола змінного струму, або імпеданс. Порівнюючи два останніх рівняння, отримуємо вираз для імпедансу Z. При послідовному увімкненні в коло змінного струму активного опору, індуктивності і ємності повний опір кола (імпеданс) дорівнює:

. (4.77)

Зсув фаз  між силою струму і напругою визначається із трикутника напруг (мал. 4.36):

. (4.78)

Із (4.77) бачимо, що при X_С = X_L реактивний опір  L – – 1/С дорівнює нулю, а імпенданс Z дорівнює активному опору R. У цьому випадку tg = 0 і  = 0. Це означає, що сила струму I і напруга U змінюються в однакових фазах. Цей випадок має назву резонансу напруг. При резонансі напруг частота генератора збігається з власною частотою, тобто задовольняє формулу Томсона.

При паралельному з’єднанні ємності C, індуктивності L та активного опору R імпеданс Z можна знайти із співвідно­шен­ня

. (4.79)

У випадку рівності ємнісного та індуктивного опорів при паралельному сполученні спостерігається резонанс стру­мів. Опір кола при цьому буде максимальним, а сила струму мінімальною, хоча струми через конденсатор та котушку можуть бути достатньо великими, однак вони вза­ємо­врівноважуються.

4.4.4. Імпеданс біологічних тканин

Як показує експеримент, для біологічних тканин характерні ве­ликі значення кута зсуву фаз між силою струму і напругою, причо­му сила струму випереджає за фазою напругу. Це свідчить, що частка ємнісного опору в біологічних об’єк­тах значна. Наведемо деякі значення кута зсуву фаз  при частоті 1 кГц для різних біооб’єктів:

нерв жаби –64

м’яз кролика –65

шкіра жаби –55

шкіра людини –55

ламінарія –78

Як правило, індуктивністю біологічних об’єктів нехтують (при частотах  < 10¹⁰ Гц) і вважають, що їхній імпе­данс дорівнює геометричній сумі активного R і ємніс­ного X_С опорів. Для характеристики пропускання струму жи­вими клітинами використовують екві­валентні схеми, тобто такі комбінації С і R, які можуть моделювати електричні параметри біологічних тканин. Розглянемо найпростіші з них.

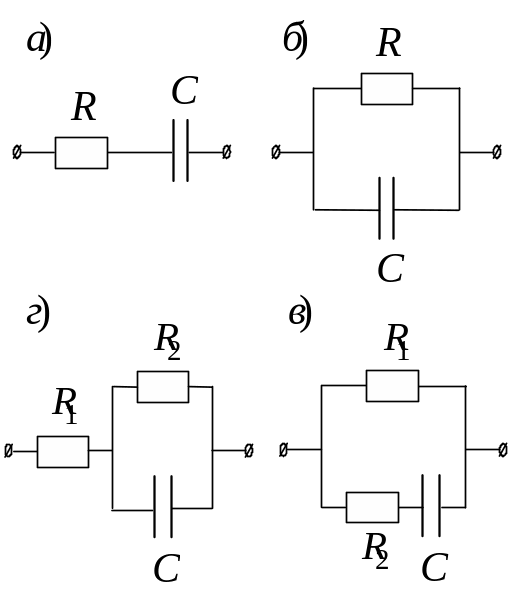
Мал. 4.37.

При послідовному сполученні R і C (мал. 4.37а) схема має суттєві розбіжності з дослідом при пропусканні постій­но­го струму. Якщо   0, то вона чинить нескінченно великий опір постійному струмові (Z₀  ), що не відповідає дійсності. Якщо ж С і R з’єднати паралельно (мал. 4.37б), то при високих частотах (  ) Z_  0, що теж не відпо­відає дійсності. Для біологічних тканин характерне більш складне поєднання ємності й активного опору. Най­більш вда­лими є схеми, що приведені на мал. 4.37в,г. При пропусканні через такі схеми високочастотного струму при   , X_C  0 їх імпеданс асимптотично наближається до деякої константи Z_ (у випадку в: Z_ = R₁R₂/(R₁ + R₂), а у випадку г: Z_ = R₁ + R₂). Ці схеми з певним наближенням можуть бути еквівалентними електричними схемами біологічних тканин, але ні одна з них не може повністю відтворювати закономірності про­пускання електричного струму через біоло­гіч­ні системи.

На мал. 4.38 приведені графіки дисперсії (частотної залеж­ності) імпедансу рослинної тка­нини: 1 – крива для нормальної здорової тканини; 2 – для на­грі­тої до t = 50C протягом 2 хв; 3 – те ж саме протягом 4 хв; 4 – після кип’ятіння в воді протягом 20 хв.

З

Мал. 4.38.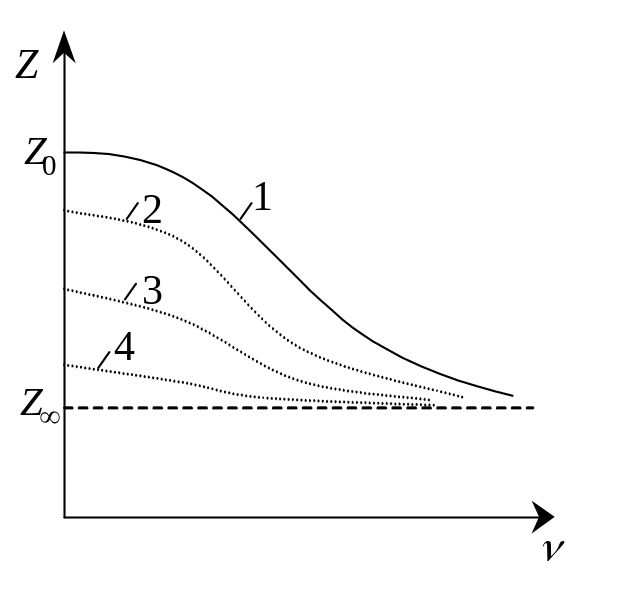

малюнка видно, що крутизна кривої в міру відмирання тка­нини зменшується, тоб­то спос­те­рігається змен­шення низькочастотного опору, то­ді як при високих частотах імпеданс практично залишається постійним. Причиною є те, що при відмиранні руй­нуються мембрани – “жи­ві конденсатори”, і нежива біологічна тканина во­лодіє суто омічним опором. Вказані особливості використовуються для оцінки фізіологічного стану об’єктів. Як правило, розраховується коефіцієнт дисперсії К, який дорівнює відно­шенню імпе­дансу при низьких частотах (10²–10⁴ Гц) до імпедансу при високих (10⁶–10⁸ Гц) частотах:

. (4.80)

У нормальних тканинах К залежить від положення організму в еволюційному ряді. Наприклад, коефіцієнт дисперсії печінки ссавців дорівнює приблизно 9–10, печінки жаби – 3–4. При відмиранні тканин вказаний коефіцієнт наближається до одиниці. Критерієм життєздатності є також частотна залежність тангенса кута зсуву фаз між силою струму і напругою. Вона дає уявлення про співвідношення між величинами активного і реактивного опорів:

tg = (X_С – X_L )/R  X_C /R.

Імпеданс тканин залежить також від їх функціонального стану, і це використовується в діагностиці. Імпеданс кровоносних судин залежить від їх кровонаповнення, а значить і від серцево-судинної діяльності. На цьому базується діаг­нос­тичний метод, який називають реографією. Реографія вивчає залежність активної складової імпедансу біологічної тканини від її деформації в процесі серцевої діяльності. Отримують реограми серця, головного мозку, магістральних судин, легень тощо. Відповідно до методики Кедрова вважається, що відносна зміна об’єму ділянки кровоносної судини (чи іншої біологічної тканини) V/V прямо пропор­ційна зміні опору R/R:

V/V  R/R.

Співвідношення між активною та реактивною складовими опору може змінюватись при зміні фізіологічного стану та деяких патологіях. Наприклад, при запаленні на перших стадіях спостерігається збільшення активного опору тканин. Цей ефект обумовлений тим, що струм низької частоти йде переважно через міжклітинну рідину, яка володіє суто омічним опором. При запаленні клітини набухають і переріз міжклітинних ділянок зменшується, що й призводить до підвищення омічного опору. Ємнісний опір при цьому практично не змінюється, оскільки не змінюється структура клітин. Очевидним є той факт, що за незмінного ємнісного опору збільшення омічного опору свідчить про набухання клітин, а зменшення омічного опору, навпаки, свідчить про зменшення об’єму клітин. Зворотний ефект спостерігається на ранніх стадіях онкологічних захворювань. Перетворення нормальних клітин у ракові супроводжується появою молодих клітин і підвищенням ємнісного опору.