95. Принципы моделирования реологических свойств. Модель упругого тела Максвелла, Вывод уравнения, являющегося его математической моделью.

При последовательном соединении элементов, напряжения (Р=Р₁+Р₂=…=Р_n) будут равны, деформации и скорости деформации будут суммироваться. (γ= γ₁+γ₂+…+ γ_n ; γ= γ·₁+ γ·₂+…+ γ·_n)

При параллельном соединении элементов – напряжения будут суммироваться (Р=Р₁+Р₂+…+Р_n), деформации и скорости деформации будут равны (γ= γ₁=γ₂=…= γ_n ; γ= γ·₁= γ·₂=…= γ·_n)

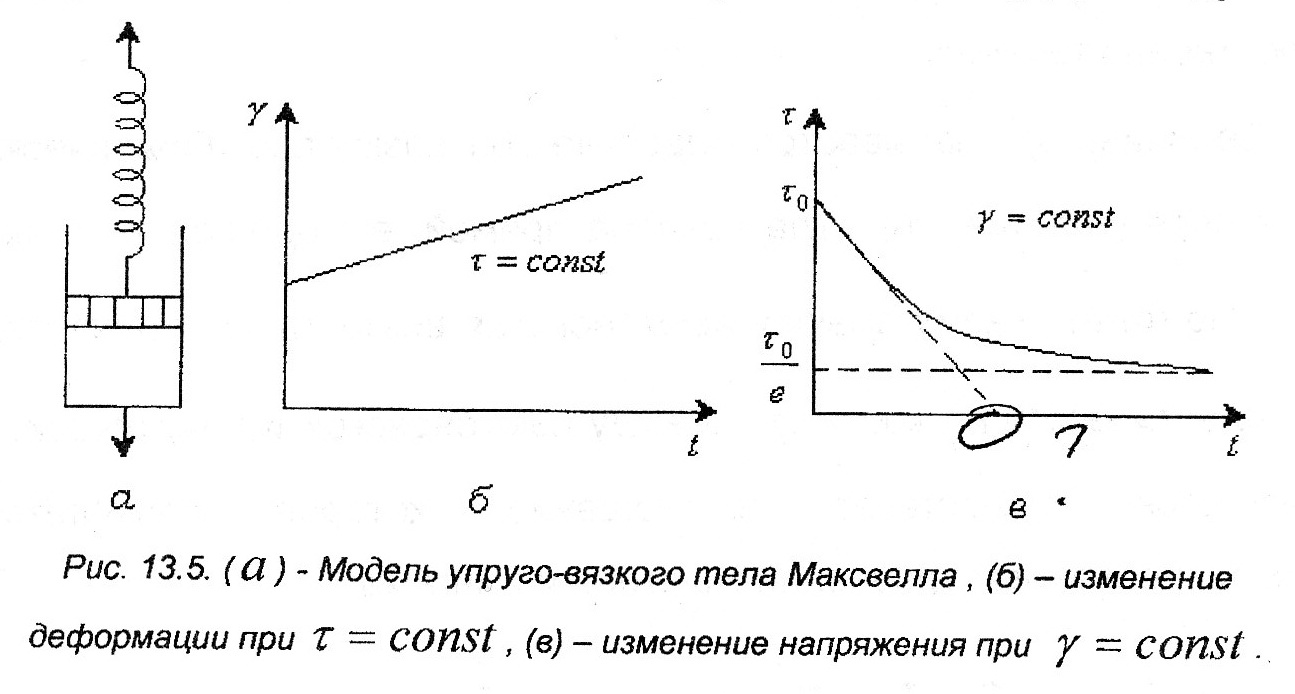Модель упруго-вязкого тела Максвелла:

Жидкие и твердые тела – одинаковая сила сцепления.

Максвеллом было дано представление, что

механические свойства тел являются

промежуточными между идеально жидкими и

идеально твердыми телами. Последовательное

соединение элементов Гука и Ньютона.

Р=Рг=Рн γ= γг+ γн

d γ/dτ = d γг/dτ = d γн/dτ

γ = Р/Е + Рτ/η – деформация. Скорость деформации: d γ/dτ = 1/Е ·d l/dτ + Р/η

1/Е · dP/ dτ + Р/η = 0 dP/P=E/η · dτ; Интегрируем получаем: ln (P/P₀)= – E/η · τ

P=P₀ · e^-τ/λ – математическая модель Максвелла.,λ – время за которое напряжение в образце уменьшается в е раз. Характерна необратимая деформация тела.λ>>τ – релаксирует очень медленно (твердое тело), жидкое тело может вести себя как твердое.λ<<τ – тело ведет себя как жидкое, твердое тело может вести себя как жидкое.

96. Модель вязкопластического тела Бингама. Пластическая вязкость.

Комбинация всех трех моделей реологии:

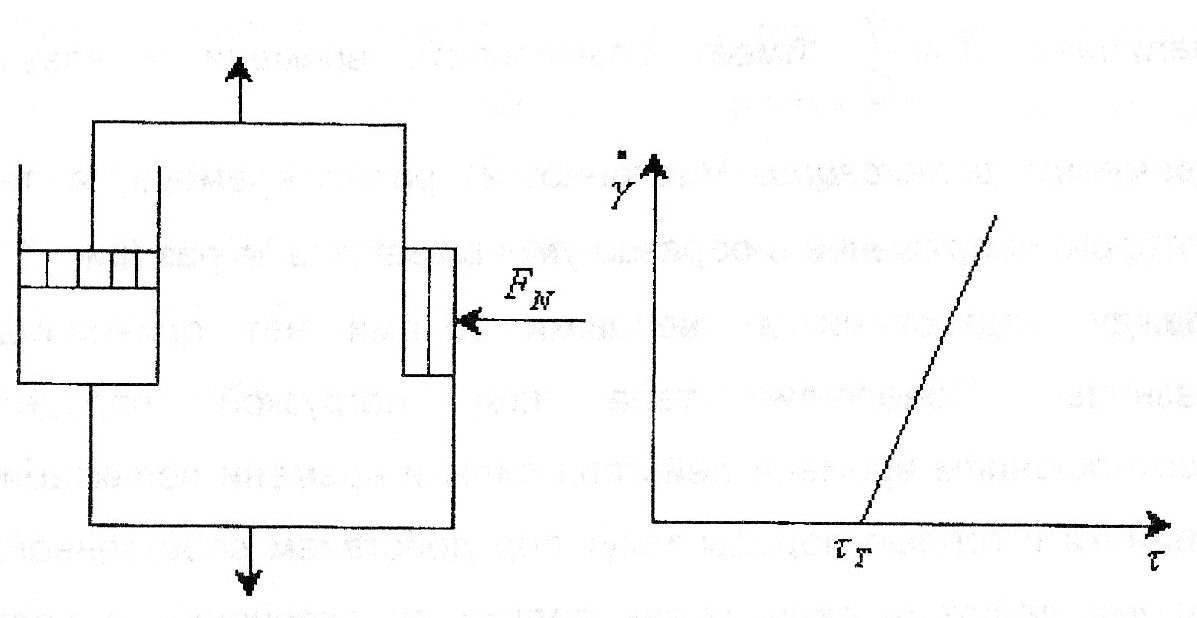(напряжение) Р<Р_Т (предела текучести) – деформация не

происходит в системе (теле) P>P_T – течение в системе

Р=Р_Т + η* · γ· – уравнение Бингама

P<P_T (деформация)γ<0 η* - пластическая вязкость

P>P_T γ↑ (скорость деформации) γ·↑

Р = η · γ· → η = Р/ γ·= (Р_Т + η* · γ·)/ γ· = η* + Р_Т/ γ·

η – сопротивление течению всей системы; η*– течение и разрушение структуры

97. Причина неподчинения дисперсных систем закону Ньютона. Кривые течения реальных дисперсных систем. Уравнение Оствальда – Вейля.

На основе реологических свойств, тела можно разделить на жидкообразные и твердообразные.

Жидкообразные тела (Р_Т=0) можно разделить на:

Ньютоновские – системы, вязкость которых не зависит от напряжения сдвига, являющегося константой. К Ньютоновским жидкостям относятся разбавленные системы с равноосными (симметричными) частицами.

Неньютоновские – системы не подчиняющиеся закону Ньютона, вязкость зависит от напряжения сдвига; псевдопластические, дилантантные жидкости. Псевдопластические жидкости – суспензии, содержащие ассиметричные частицы, растворы полимеров. При увеличении напряжения сдвига, течение будет убыстряться. Дилантантные жидкости – дисперсные системы с большим содержанием твердой дисперсной фазы. При увеличении напряжения сдвига растет вязкость.

Неньютоновские жидкости описываются уравнением Оствальда – Вейда: Р = k · γ·

1 – Ньютоновские жидкости 1 – бингамовское тело

2- псевдопластическое твердообразное тело 2 – Псевдопластические

3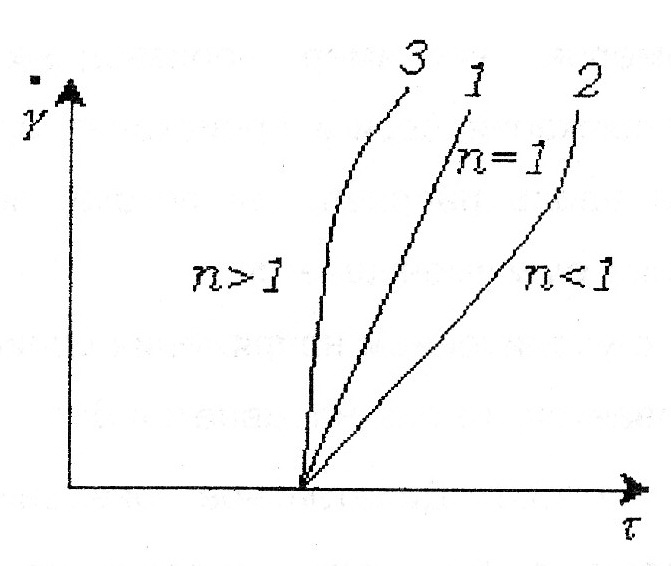 – пластическое дилантантное тело 3 – Дилантантные жидкости