1. Постановка транспортного завдання лінійного програмування.

Розглянемо наступну ситуацію:

якийсь однорідний продукт (наприклад, цукровий пісок) повинен бути доставлений від декількох постачальників до декількох споживачів; точніше: є m постачальників, що містять, відповідно, a₁,...,a_m кг якогось однорідного продукту, і n споживачів, що вимагають, відповідно, b₁,...,b_n кг цього ж продукту (замість кг можуть бути будь-які інші кількісні одиниці). Організація доставки продукту являє собою призначення чисел x_ij, i=1,...,m, j=1,...,n таких, що x_ij - кількість продукту, яку треба доставити від постачальника № i споживачеві № j ; відома ціна c_ij перевезення одиниці продукту від постачальника № i споживачеві № j; таким чином, сумарна вартість перевезень в описаній ситуації є число

;

потрібно знайти такі числа x_ij, щоб зазначена вище сумарна вартість виявилася мінімальною.

У цьому й складається транспортне завдання лінійного програмування. Помітимо, що це - дійсно завдання лінійного програмування. Адже в ній потрібно знайти мінімум нелінійної функції при наступних обмеженнях, очевидних з погляду здорового глузду:

(12.1.1)

Можна перетворити ця умова в таке, при якому стає застосовним симплекс - метод і відповідь виникне автоматично. Однак, у даній конкретній ситуації існує принципово інший алгоритм рішення, набагато більше «короткий» за часом і обсягом обчислень.

12.2. Термінологія транспортного завдання лінійного програмування

Нам буде потрібно кілька термінів для опису згаданого вище алгоритму.

Насамперед, запишемо вихідну інформацію для транспортного завдання у вигляді наступної таблиці:

c11 x11	...	c1j x1j	...	c1n x1n	a1
...	...	...	...	....	...
ci1 xi1	...	cij xij	...	cin xin	ai
...	...	...	...	...	...
cm1 xm1	...	cmj xmj	...	cmn xmn	am
b1	...	bj	...	bn

Зміст елементів таблиці очевидний. Набір чисел x_ij називається планом перевезень. Якщо ці числа задовольняють всім обмеженням транспортного завдання (тобто умовам (12.1.1)), то план називається припустимим. Якщо деякий припустимий план дає мінімум ціни, то він називається оптимальним.

Прийнято умови (12.1.1) переписувати в трохи іншому виді. А саме, розглянемо числа a₁,...,a_m, b₁,...,b_n; будемо вважати, що

(12.2.1) ;

якщо це не так і, скажемо, , то введемо мнимого споживача із запитом b_n+1= ; якщо ж , те введемо мнимого постачальника із запасом a_m+1= . Для мнимих постачальника й споживача вартість перевезень покладається рівної нулю. Таким чином, у кожному разі можна вважати, що таблиця з початку цього пункту задовольняє умові (12.2.1). Крім того, без втрати спільності можна вважати, що умови (12.1.1) є наступними:

(12.2.2)

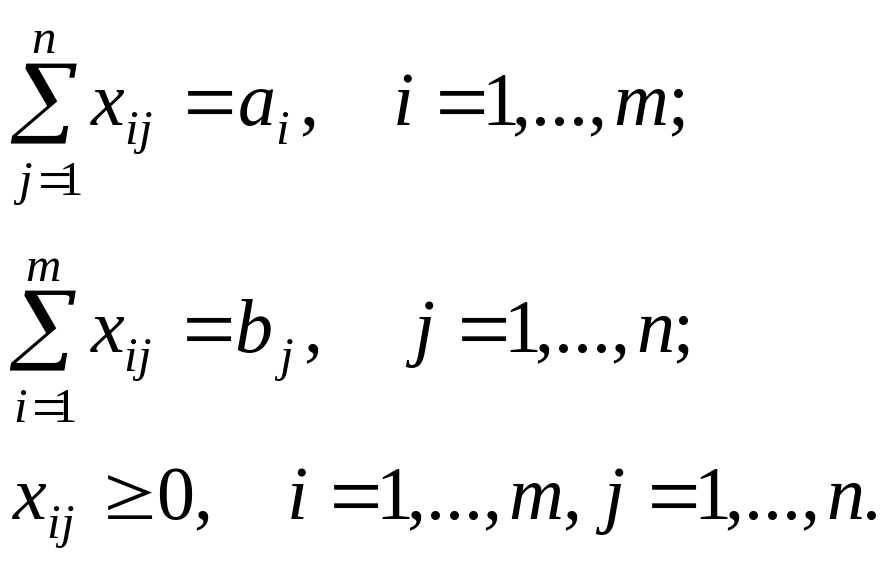
Дійсно, якщо вдасться відшукати оптимальний план при умовах (12.2.2), те завдання буде вирішена.

Отже, транспортним завданням лінійного програмування називається завдання пошуку мінімуму функції

;

при обмеженнях (12.2.2) у припущенні, що справедливо умову (12.2.1).