1. Задача апроксимації функції.

Нехай на відрізку [a,b] деяка функція f(x) задана лише в деяких точках , тобто відомі її значення , які, як правило, збирають у таблицю:

x	x0	x1	...	xn
f(x)	y0	y1	...	yn

Крім того, нехай задана деяка точка . Задача апроксимації функції полягає в тому, щоб по наявній таблиці знайти число з відомим ступенем точності. Слово «апроксимація» означає «наближення».

Легко зрозуміти, що якщо на функцію не накладаються ніякі додаткові умови, то постановка задачі безперспективна. Ми будемо далі припускати, що функція має всі похідні. Виявляється, що в цьому випадку по наявним n+1 значенням можна знайти ще одне й оцінити, наскільки воно точно.

2. Інтерполяційний багаточлен Лагранжа й різні форми його запису.

Будемо виходити з таблиці в попередньому пункті. Побудуємо по ній наступний багаточлен:

.

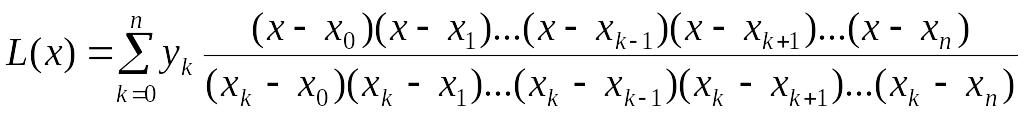Для ясності треба помітити, що в цій сумі - ( ) доданків, що в що складається № k у чисельнику рівно множників і що кожний з них є багаточленом ступеня n. Цей багаточлен називається багаточленом Лагранжа таблиці значень функції.

От його основні властивості:

1. це - багаточлен ступеня ;

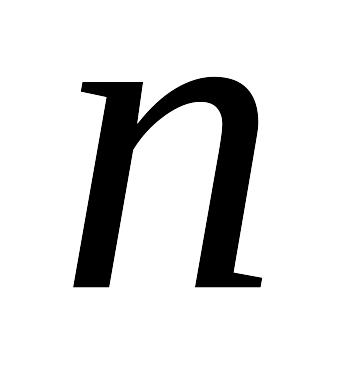2) , тобто багаточлен Лагранжа має в точках ті ж значення, що

і функція ;

3) якщо фіксувати будь-яке число те виявиться виконаним нерівність

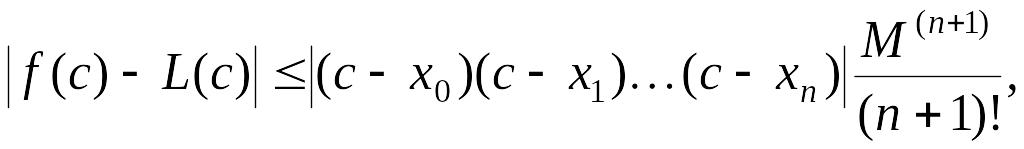
де на ділянці , тобто число обмежує похідну го порядку функції .

Сказане означає, що якщо функція задана своєю таблицею й потрібно знайти значення десь у проміжній точці c, те можна по таблиці побудувати багаточлен Лагранжа і його значення в цій точці прийняти за значення функції; помилка, що при цьому виникне, може бути оцінена за допомогою формули, написаної вище в п.3).

Відшукання проміжного значення функції називається інтерполяцією; коли це робиться за допомогою багаточлена Лагранжа, то говорять про інтерполяційний багаточлен Лагранжа або про інтерполяцію по Лагранжу.

Зауваження. Можна довести, що існує один і тільки один багаточлен ступеня n, що у заданих n+1 точках приймає задані значення. Тому багаточлен Лагранжа - це всього лише одна з форм запису того самого єдиного багаточлена ступеня n, що визначається таблицею з п.1.

3. Задача рівномірного наближення функції.

Як і раніше будемо виходити з таблиці значень функції з п.1. Вище ми розглянули задачу інтерполяції функції, що складалася в заміні даної функції іншої, значення якої в крапці інтерполяції й приймається за наближене значення самої функції. Метод Лагранжа полягає в тому, щоб підміну одного числа іншим виявилося можливим оцінити.

Існує інший підхід, іменований рівномірним наближенням. При цьому підході теж відбувається заміна значення на значення деякої функції , причому виявляється можливим оцінити помилку цієї підміни. Будується функція в такий спосіб.

Для здійснення рівномірного наближення повинна бути задана не тільки таблиця з п.1, але й деякий клас функцій G усередині якого й буде виділена функція . Уведемо величину

,

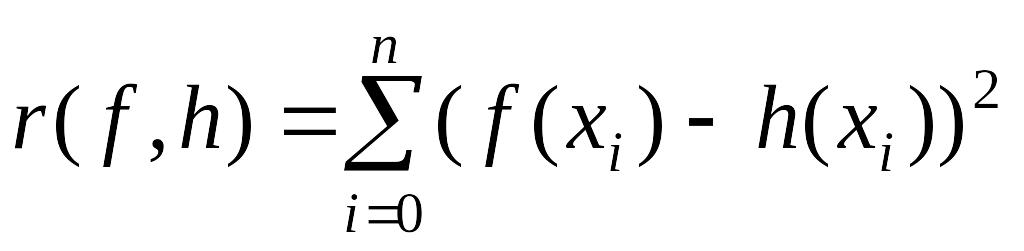у якій числа беруться з таблиці в п.1, а числа для кожної функції із класу G передбачаються обчислюваними. Функція вибирається як доставляє мінімум величині . Цю функцію називають найкращим рівномірним наближенням функції із класу G. Звичайно, як оцінити різниця в такій ситуації, - це окрема тема, тісно зв'язана як із природою класу G, так і з таблицею з п.1.