Лекция 16 моделювання стохастичних систем приклад реалізації методу найшвидшого спуска рішення основного завдання опуклого програмування.

Потрібно знайти мінімум функції

при обмеженнях

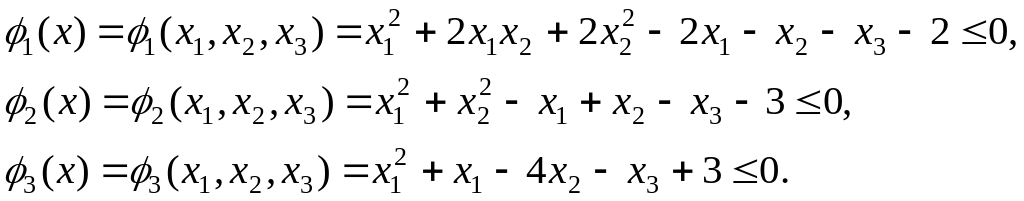
Зміст того, що буде зроблено нижче - доставити матеріал для контрольного приклада до програми, що реалізує метод найшвидшого спуска.

Для початку потрібно знайти нульове наближення й фіксувати початкову точність Будемо вважати, що точку знайшли «на око» - це точка =(1,-1,9). У цьому випадку

.

Покладемо =0.5. Тоді

.

Визначаємо напрямок спуска . Для цього вирішуємо завдання лінійного програмування:

при обмеженнях:

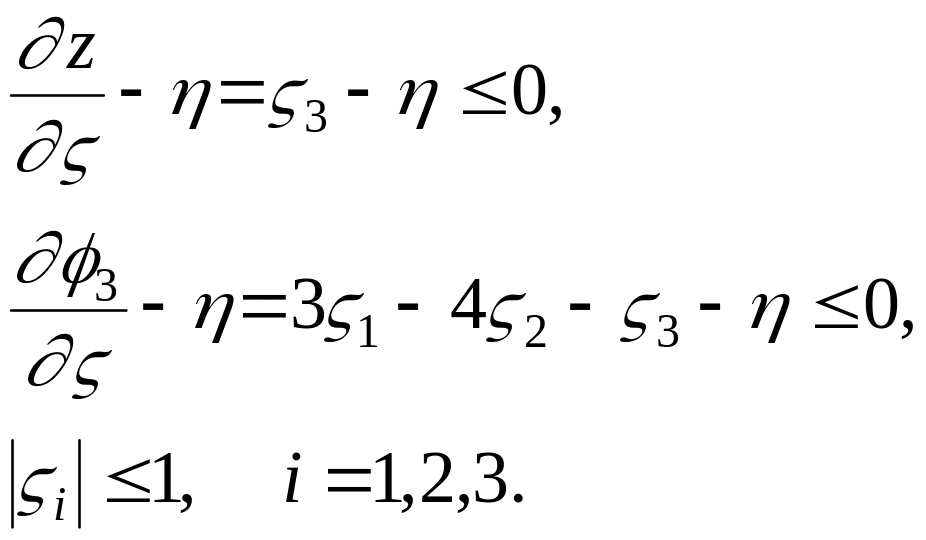
Нагадаємо, що похідні по напрямку вважаються в точці , а також те, що нерівність являє собою пару нерівностей: або, що те ж саме, . Крім того, помітимо, що змінні в обговорюваній ситуації - це координати вектора; тому важливо лише, щоб вони були хоч якось обмежені по модулі (не обов'язково саме числом 1); важливий лише сам факт їхньої обмеженості по модулі в обговорюваному завданні. Тому обсяг обчислень у даному конкретному прикладі скоротиться, якщо помітити, що з умов і інших обмежень треба, що й змінна обмежено. Отже, можна зменшити обсяг вихідної інформації (саме в цьому випадку) і сформулювати завдання так:

при обмеженнях:

Вирішивши це завдання, одержимо:

Обчислимо тепер Маємо: . Отже, .

Далі варто визначити крок . Для цього фіксують пряму

.

Далі відшукується найменший з позитивних корінь рівнянь

.

Ним виявляється .

Нарешті, визначимо нове наближення по формулі

.

Тепер треба повторити всі спочатку, замінивши на й на . Одержимо (у відповідному завданні лінійного програмування знову можна буде видалити обмеження ):

Тому . Рухаючись по тій же схемі (у даному прикладі вдається щораз не включати умову , що полегшує процес рішення), ми будемо одержувати:

Упевнимося тепер, що точка є рішенням завдання. Для цього, прийнявши її за чергове наближення, спробуємо знайти наближення наступне. Маємо:

Знайдемо тепер похідні по напрямку

у точці . Одержимо:

Тепер формулюємо завдання лінійного програмування:

при обмеженнях:

(Тут теж немає умови тільки через особливості даного приклада.) Одержимо: А це й означає, що точка (0;1;-1) - рішення.

Лекція 17

МОДЕЛЮВАННЯ ТА ОПТИМІЗАЦІЯ ТИПОВИХ

ПРОЦЕСІВ ТЕПЛО- ТА МАСООБМІНУ.

ОСНОВНЕ ЗАВДАННЯ КВАДРАТИЧНОГО ПРОГРАМУВАННЯ Й АДАПТАЦІЯ МЕТОДУ НАЙШВИДШОГО СПУСКА ДО ЇЇ РІШЕННЯ.

1. Квадратичні форми і їхні різновиди.

Квадратичною формою називається вираження

,

у якому - змінні, а матриця складається із чисел, які називаються коефіцієнтами квадратичної форми. Прийнято вважати, що матриця симетрична, тобто Коли квадратична форма звертається в нуль тільки на нульових значеннях змінних, неї називають певною; у противному випадку квадратична форма називається невизначеної. Якщо квадратична форма, будучи певної, приймає тільки ненегативні значення, то неї називають позитивно певної, а якщо всього її значення менше або дорівнюють нулю, то вона називається негативно певної.

Коли у вираженні

для всіх виконуються рівності , говорять, що вид квадратичної форми - діагональний. Очевидно, що при діагональному виді квадратичної форми безпосередньо із цього виду можна усвідомити, чи є форма певної й, якщо так, те якого знака. У загальному ж випадку для відповіді на таке питання прийнято спочатку привести квадратичну форму до діагонального виду. Нагадаємо, що мається на увазі під цією дією.

Виділимо у квадратичній формі всі доданки, що містять змінну :

.

Припустимо спочатку, що . Тоді виділену групу доданків можна перетворити так:

.

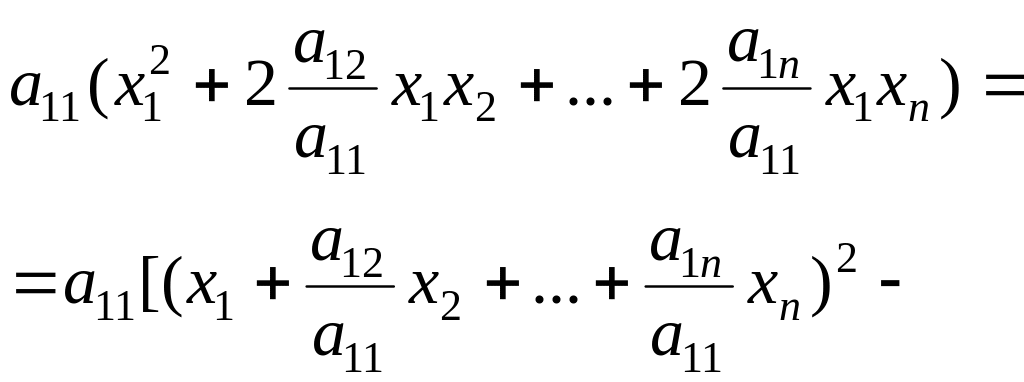
Якщо тепер позначити , то вихідну квадратичну форму можна переписати у вигляді:

,

після чого описану процедуру треба застосувати до тої частини квадратичної форми, що описана під знаком останньої суми. І так далі, поки не вийде діагональний вид.

У тім же випадку, коли у вираженні коефіцієнт , вибирають будь-який , не дорівнює нулю й думають:

Після такої заміни вже виникає доданок з і стає застосовна описана раніше схема.