
- •Конспект лекцій Частина іі з дисципліни “Числові методи і моделювання на еом”
- •Симплекс-Метод для відшукання опорного рішення
- •Приклад відшукання опорного рішення.
- •Симплекс-Метод для відшукання оптимального рішення.
- •Приклад відшукання оптимального рішення
- •Задача апроксимації функції.
- •Інтерполяційний багаточлен Лагранжа й різні форми його запису.
- •Задача рівномірного наближення функції.
- •11.4. Метод найменших квадратів.
- •Багаточлени Бернштейна.
- •Постановка транспортного завдання лінійного програмування.
- •12.2. Термінологія транспортного завдання лінійного програмування
- •Опис методу потенціалів рішення транспортного завдання лінійного програмування
- •Лекция 13
- •Аналіз періодичності послідовностей. Приклад рішення транспортної задачі методом потенціалів
- •Лекция 14 методи розв’язку оптимізаційних задач. Основне завдання опуклого програмування: термінологія й формулювання.
- •Опуклі множини й опуклі функції
- •Формулювання основного завдання опуклого програмування
- •Канонічна форма основного завдання опуклого програмування
- •Пошук вихідного наближення.
- •Лекція 15 моделювання лінійних систем. Метод найшвидшого спуска вирішення основної задачі опуклого програмування
- •Лекция 16 моделювання стохастичних систем приклад реалізації методу найшвидшого спуска рішення основного завдання опуклого програмування.
- •Квадратичні форми і їхні різновиди.
- •Формулювання основного завдання квадратичного програмування.
- •17.3. Рішення основного завдання квадратичного програмування.
- •Приклад рішення основного завдання квадратичного програмування.
- •Лекція 18 програмні засоби моделювання на еом
- •18.1. Програмне забезпечення задач про наближення функцій.
- •18.2. Основні методи пошуку найкращого рівняння
- •Список рекомендованої літератури
Пошук вихідного наближення.
Як відзначалося в п.2, пошук рішення основного завдання опуклого програмування являє собою побудова послідовності точок в n-мірному просторі, що сходиться до точки екстремальної (шуканої). Пояснимо це. Якщо - шукана екстремальна точка й
![]() ,
,
де послідовність прагне до точки »
означають, що числова послідовність
![]()
прагне до нуля.
Початок
згаданої послідовності точок - точка
![]() - називається початковим
наближенням.
Ми опишемо зараз спосіб знайти
.
- називається початковим
наближенням.
Ми опишемо зараз спосіб знайти
.
Нехай
спочатку m=1.
Щоб знайти точку a
таку, що
![]() ,
можна діяти, наприклад, так: шукати
мінімум функції багатьох змінних. Або
інший спосіб: покласти всі координати,
крім однієї, рівними конкретним числам,
а що залишилася підібрати, відповідно
до вимоги.
,
можна діяти, наприклад, так: шукати
мінімум функції багатьох змінних. Або
інший спосіб: покласти всі координати,
крім однієї, рівними конкретним числам,
а що залишилася підібрати, відповідно
до вимоги.
Припустимо,
що для m=k
відшукання крапки a
такий, що
![]() вже відбулося. Тоді пошук точки a,
для якої буде виконана ще одна умова -
вже відбулося. Тоді пошук точки a,
для якої буде виконана ще одна умова -
![]() - можна розглядати як пошук точки мінімуму
опуклої функції
- можна розглядати як пошук точки мінімуму
опуклої функції
![]() при обмеженнях
при обмеженнях
![]() .
Знайдена екстремальна точка буде,
звичайно, задовольняти всім необхідним
нерівностям (нагадаємо, що споконвічно
передбачається випадок наявності
внутрішньої точки!)
.
Знайдена екстремальна точка буде,
звичайно, задовольняти всім необхідним
нерівностям (нагадаємо, що споконвічно
передбачається випадок наявності
внутрішньої точки!)
Процедура пошуку мінімуму в завданні опуклого програмування буде описана в наступній лекції. Як уже згадувалося, вона виходить тільки з початкового наближення . Тому описаний тут спосіб побудови цього початкового наближення фактично звівся до двох процедур:
Процедура
1.
Знайти точку, що задовольняє єдиній
нерівності
![]() .
Нехай це буде крапка
.
Нехай це буде крапка
![]() .
.
Процедура 2. Знайти екстремальну точку в кожному з наступних завдань опуклого програмування:
Завдання
1.
Цільова функція
![]() ,
умови:
.
Початкове наближення - точка
.
Нехай результатом буде точка
,
умови:
.
Початкове наближення - точка
.
Нехай результатом буде точка
![]() .
.
Завдання
2.
Цільова функція
![]() ,
умови
,
умови
![]() .
Початкове наближення - точка
.
Нехай результатом буде точка
.
Початкове наближення - точка
.
Нехай результатом буде точка
![]() .
.
Завдання
3.
Цільова функція
![]() ,
умови
,
умови
![]() ..
Початкове наближення - точка
.
Нехай результатом буде точка
..
Початкове наближення - точка
.
Нехай результатом буде точка
![]() .
.
І так далі, аж до відшукання початкового наближення .
Принципове зауваження. Якщо на одному з описаних етапів мінімум цільової функції виявиться позитивним, те, як легко помітити, процедура переривається, тому що позитивність мінімуму означає відсутність шуканої точки.
Лекція 15 моделювання лінійних систем. Метод найшвидшого спуска вирішення основної задачі опуклого програмування
Збережемо
термінологію й позначення попередньої
лекції. Таким чином, ми будемо будувати
послідовність точок
в
![]() -мірному
просторі, що сходиться до вирішення
основного завдання опуклого програмування:
-мірному
просторі, що сходиться до вирішення
основного завдання опуклого програмування:
![]() .
.
Описуваний нижче метод називається методом найшвидшого спуска.
Крок
1.
Фіксуємо довільне число
![]() .
Будемо надалі називати його точністю
наближення.
Воно буде використовуватися тільки на
наступному кроці.
.
Будемо надалі називати його точністю
наближення.
Воно буде використовуватися тільки на
наступному кроці.
Фіксуємо, далі, початкове наближення . Якщо серед нерівностей
![]()
є
хоч одна реальна рівність, то переходимо
до наступного кроку. Якщо ж рівностей
ні, то покладемо
![]() й розглянемо точки
й розглянемо точки
![]() при довільно мінливому параметрі
при довільно мінливому параметрі
![]() .
Серед корінь рівнянь відносно
.
Серед корінь рівнянь відносно
![]()
![]()
виберемо
мінімальний позитивний
![]() і фіксуємо точку
і фіксуємо точку
![]() .
.
Можна довести, що ця точка теж задовольняє всім нерівностям
![]() ,
,
але
при цьому хоч одне із цих нерівностей
є точною рівністю. Тому далі ми припускаємо,
що початкове наближення
,
замінене, при необхідності, на
![]() ,
перетворює в рівність хоча б одне з
даних обмежень.
,
перетворює в рівність хоча б одне з
даних обмежень.
Крок
2.
Відберемо ті функції
![]() ,
для яких
,
для яких
![]() .
Саме завдяки вибору
.
Саме завдяки вибору
![]() такі функції - хоча б одна! - є. Нехай це
будуть функції
такі функції - хоча б одна! - є. Нехай це
будуть функції
![]() .
.
Крок
3.
Цей крок називається визначенням
напрямку спуска.
Його вихідним продуктом буде набір
чисел
![]() .
.
Побудуємо наступне завдання лінійного програмування:
нехай
символи
![]() позначають n+1
незалежних змінних; потрібно знайти
мінімум функції
позначають n+1
незалежних змінних; потрібно знайти
мінімум функції
![]()
при обмеженнях:

Можна
довести, що це завдання обов'язково має
рішення. Нехай
![]() і
і
![]() - екстремальна точка цього завдання й
- екстремальна точка цього завдання й
![]() саме й дорівнює
саме й дорівнює
![]() .
.
Крок
3.
Цей крок називається обчисленням
нового значення точності
![]() .
Нам має бути визначити для подальшого
нове число - число
.
Нам має бути визначити для подальшого
нове число - число
![]() .
Можливі два випадки:
.
Можливі два випадки:
![]() і
і
![]() .
.
У
першому випадку покладемо
![]() й переходимо до наступного кроку.
й переходимо до наступного кроку.
Розглянемо
другий випадок:
![]() .
Якщо -
.
Якщо -![]() , то думаємо
, то думаємо
![]() й переходимо до наступного кроку. Якщо
ж
й переходимо до наступного кроку. Якщо
ж
![]() (а це єдина можливість, що залишилася!),
то виділимо серед обмежень
(а це єдина можливість, що залишилася!),
то виділимо серед обмежень
![]()
всі
такі
![]() ,
для яких
,
для яких
![]() .
Потім сформулюємо завдання лінійного
програмування:
.
Потім сформулюємо завдання лінійного
програмування:
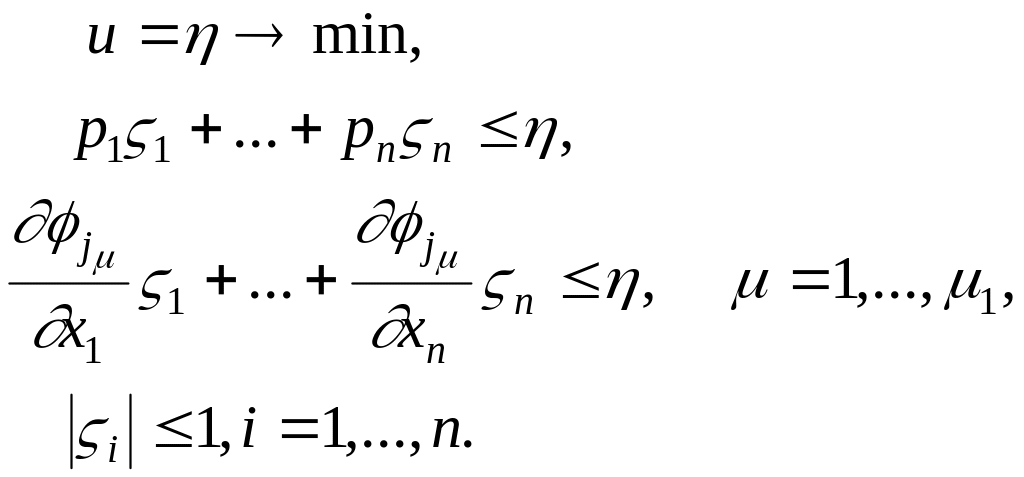
Вирішимо
це завдання й нехай мінімум цільової
функції дорівнює
![]() . Якщо виявилося, що
. Якщо виявилося, що
![]() =0,
те
-
рішення й процедура кінчена (це, зрозуміло,
доказуваний факт). Якщо ж
<0
(а це єдина можливість, що залишилася!),
то думаємо
=0,
те
-
рішення й процедура кінчена (це, зрозуміло,
доказуваний факт). Якщо ж
<0
(а це єдина можливість, що залишилася!),
то думаємо
![]() і
переходимо до наступного кроку.
і
переходимо до наступного кроку.
Крок
4.
Цей крок називається обчисленням
кроку
![]() .
Розглянемо змінну точку
.
Розглянемо змінну точку
![]() ,
у якій
-
мінлива змінна. Вирішимо відносно
кожне з рівнянь
,
у якій
-
мінлива змінна. Вирішимо відносно
кожне з рівнянь
![]() .
.
Виберемо
серед сукупності всіх корінь всіх цих
рівнянь мінімальний позитивний корінь.
Нехай це буде число
![]() .
Це число є шуканим на обговорюваному
кроці й називається кроком
наближення.
.
Це число є шуканим на обговорюваному
кроці й називається кроком
наближення.
Крок 5. Визначення нового наближення. Покладемо
![]() .
.
Ця точка є шуканою на даному кроці.
Помітимо
тепер, що на початку побудови в нас були
крапка
й число
![]() ,
а наприкінці проведених кроків виникли
точка
,
а наприкінці проведених кроків виникли
точка
![]() й число
й число
![]() .
Тепер повторимо всі проведені кроки,
замінивши пари
,
.
Тепер повторимо всі проведені кроки,
замінивши пари
,![]() на парі
на парі
![]() ,
,
![]() .
У результаті виникне пари
.
У результаті виникне пари
![]() й т.д. Таким чином, виявиться побудованої
послідовність наближень
й т.д. Таким чином, виявиться побудованої
послідовність наближень
![]() ,
про яку говорилося спочатку.
,
про яку говорилося спочатку.
Переривання обчислень. На практиці, зрозуміло, послідовність
будується
не нескінченної, а кінцевої. Якщо на
якімсь етапі виникає ситуація
![]() ,
те це означає, що
,
те це означає, що
![]() - точне рішення (тобто
- шукана екстремальна точка).
- точне рішення (тобто
- шукана екстремальна точка).
Крім того, має місце наступний математичний факт:
нехай
![]() -
чергове
наближення, отримане відповідно до
описаного вище методикою; фіксуємо
наступне завдання лінійного програмування:
-
чергове
наближення, отримане відповідно до
описаного вище методикою; фіксуємо
наступне завдання лінійного програмування:
![]()
при обмеженнях:

тут
частки похідні обчислені в крапці
![]() ;
тоді
мінімум, шуканий у цьому завданні, більше
або дорівнює числу
;
тоді
мінімум, шуканий у цьому завданні, більше
або дорівнює числу
![]() .
.
Звідси виникає можливість відслідковувати точність чергового наближення; як тільки чергове наближення виявиться досить близьким до дійсного мінімуму, обчислення припиняють.
