Закінчення табл.3.1
-
1
2
3
4
1976
5,03
6,04
5,78
1977
6,78
6,14
6,36
1978
6,90
5,99
6,83
1979
5,94
6,02
6,04
1980
5,30
5,99
5,23
1981
5,18
5,99
5,49
1982
6,61
6,18
6.32
1983
6,94
6,37
7,01
1984
6,87
6,67
6,72
1985
6,25
6,86
6,43
1986
6,66
6,70
5,30
1987
7,58
6,73
6,92
1988
6,13
6,83
6,83
1989
7,01
-
6,80
1990
6,79
-
6,78
3.3. Метод найменших квадратів
Серед багатьох методів прикладної статистики для визначення параметрів тренду динамічного ряду найчастіше використовують метод найменших квадратів, розроблений Гауссом і Лежандром на початку минулого століття.
Припустимо, що в результаті попереднього аналізу певного соціально-економічного явища його основна тенденція динаміки описується многочленом р-го порядку виду
(3.13)
Суть методу найменших квадратів полягає в мінімізації суми квадратів відхилень фактичних рівнів ряду від вирівняних
(3.14)
де п - число рівнів ряду динаміки; - фактичні значення рівнів ряду; - теоретичні (розрахункові чи вирівняні) значення рівнів, здобуті за формулою (3.13).
Надалі індекс підсумовування для спрощення запису будемо опускати.
Щоб знайти значення невідомих параметрів a0, a1, a2, …ap, необхідно прирівняти частинні похідні суми (3.14) за заданими параметрами до нуля. Після нескладних перетворень дістаємо систему (р + 1) нормальних рівнянь з (р + 1) невідомими:
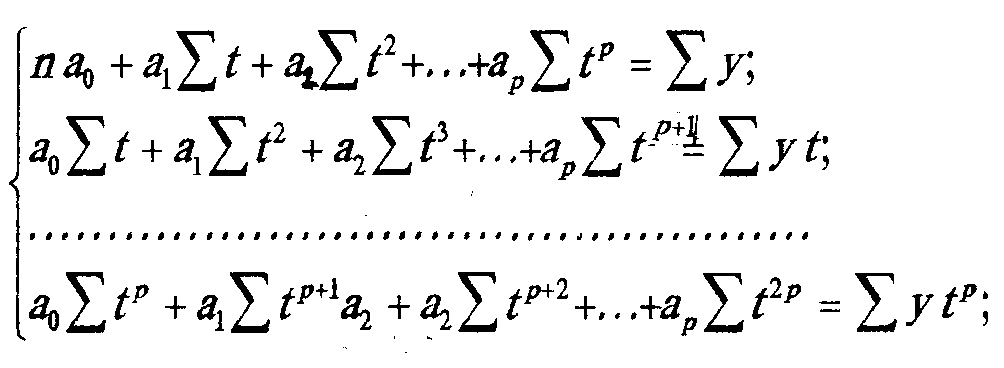(3.15)
Вибираючи
відлік часу так, щоб
=
0, систему нормальних рівнянь (3.15)
можна значно спростити. Наприклад,
для парних значень степенів р
вона матиме вигляд
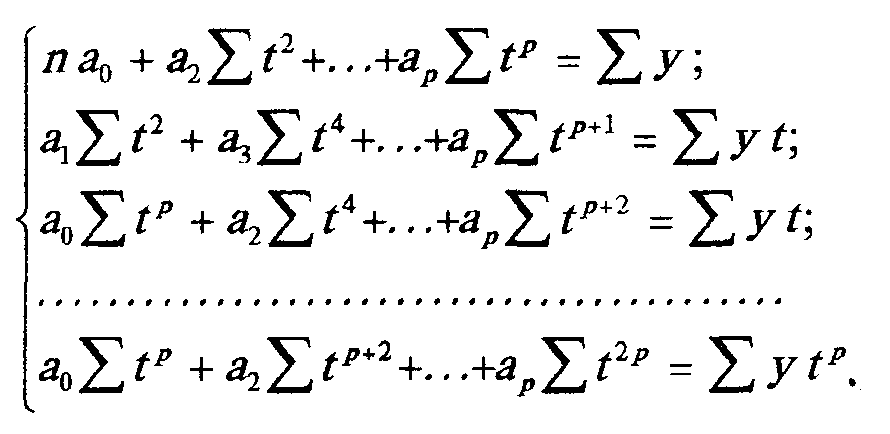(3.16)
Проте,
розв'язуючи рівняння регресії, можна і
не прирівнювати
до
нуля, а вести відлік часу t
від нуля до n.
У загальному випадку розв'язування
системи рівнянь (3.15) також можна спростити,
оскільки величини
не пов'язані з рівнями ряду динаміки.
Якщо рівні часових рядів рівновіддалені
один від одного, то величини
і
наступні є функціями числа рівнів n.
Використовуючи дане твердження,
дістаємо такі співвідношення:
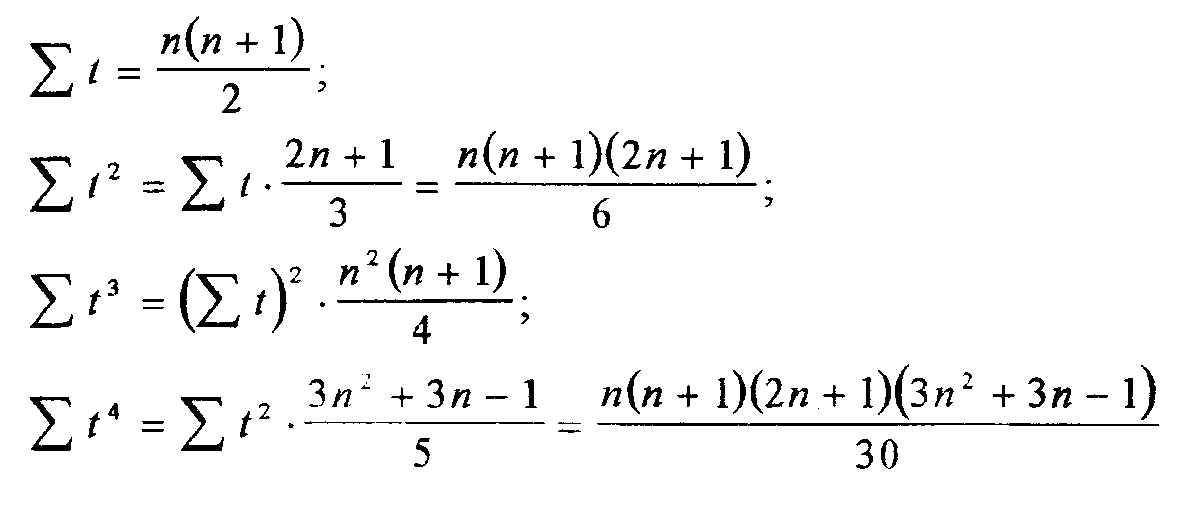
тощо.
У прикладній статистиці відомі загальні принципи вибору вихідного рівняння для згладжування рядів динаміки. Якщо прирости рівнів ряду коливаються навколо сталої величини (збільшуються в арифметичній прогресії), такий ряд вирівнюється за допомогою многочлена першого порядку (рівняння прямої). Якщо прирости приростів рівнів часового ряду коливаються навколо сталої величини, згладжування проводиться з використанням многочлена другого порядку (параболи). У випадку, коли прирости приростів рівнів часового ряду коливаються навколо відносної сталої величини (збільшуються в геометричній прогресії), часовий ряд вирівнюється з використанням показникової функції.
Розглянемо ще два способи вибору вигляду функції для опису основної тенденції ряду динаміки.
Перший спосіб полягає в тому , що на основі логічного аналізу і власного досвіду дослідник вибирає кілька різних функцій і оцінює їх параметри, після цього визначає середньоквадратичну похибку для кожної з даних функцій за формулою
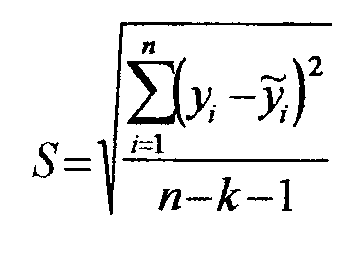(3.17)
де
уi
- фактичні
значення рівнів ряду динаміки;
- вирівняні
значення рівнів часового ряду; п
- число
параметрів функції (без вільного члена).
Функцію, для якої середньоквадратична похибка є найменшою, вважають найкращою для подання тренду.
Зауважимо, що даний метод дає порівняно добрі результати тільки тоді, коли однакова кількість параметрів рівнянь.
Другий спосіб вибору функції полягає в порівнянні дисперсій. Загальну варіацію досліджуваного ряду динаміки можна поділити на дві частини: варіацію внаслідок тенденції й випадкову варіацію, або V= V1+ V2 .
Загальну варіацію визначають за формулою
(3.18)
де у - середній рівень ряду динаміки, випадкову варіацію (варіацію навколо тенденції) - за формулою
(3.19)
де
- розрахункові значення рівнів часового
ряду.