2.4. Перевірка гіпотези про існування основної тенденції динаміки

Перш ніж визначити тренд, перевіряють гіпотезу про ге, чи існує він взагалі.

У соціально-економічних рядах динаміки можна спо­стерігати тенденцію трьох видів: середнього рівня, дисперсії й автокореляції.

Тендетуя середнього рівня легко визначається за графіками. Її можна також описати за допомогою певної функції, навколо якої змінюються фактичні рівні досліджу­ваного явища. У даному випадку значення тренду в окремі моменти часу є математичними сподіваннями часового ряду.

Тенденція дисперсії характеризує зміну відхилень між емпіричними рівнями й детерміністичною компонентою ряду. її можна подати графічно.

Тенденція автпокореляцїі виражає тенденцію зміни зв'язку між окремими рівнями ряду динаміки.

Виявити в часовому ряді наявність основної тенденції можна шляхом перевірки різниці середніх рівній і методом Форстера - Стюарта. Розглянемо кожний з цих підходів ок­ремо.

А) Перевірка різниці середніх рівнів

Найчастіше розбивають рівні часового ряду на кілька груп і перевіряють нульову гіпотезу відносно їх середніх. При відхиленні нульової гіпотези вважають, що тренд існує.

У найпростішому випадку часовий ряд поділяють на дві частини. Рівні кожної з них розглядаються як окремі вибірки відповідно із середнім значенням і .

Необхідно перевірити гіпотезу про значущість різниці. Дана гіпотеза перевіряється на основі t-статистики Стьюдента.

При рівності дисперсій досліджуваних сукупностей ( ) або незначній різниці між ними t-статистику об­числюють за формулою

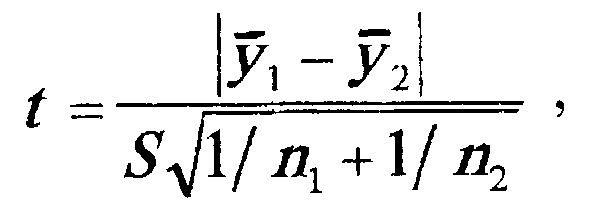(2.18)

- середні значення відповідно для першої й другої частини часового ряду; п₁, п₂ - кількість спостережень у даних частинах ряду; S - середньоквадратичне відхилення різниці середніх.

Якщо , гіпотеза про відсутність тренду (нульова гіпотеза) відхиляється, а при гіпотеза приймається (тут t - розрахункове значення статистики; t_α - табличне значен­ня статистики при рівні значущості α).

Значення t_α вбереться з числом ступенів свободи, що дорівнює ( -1). Середньоквадратичне відхилення мож­на визначити на основі середньої зваженої величини дис­персій окремих сукупностей ряду за формулою

(2.19)

Оцінюючи дисперсії і для першої та другої су­купностей, числа ступенів свободи беруть такими, що дорів­нюють відповідно (n₁ - 1) і (n₂ - 1).

Гіпотеза про рівність дисперсій перевіряється з допо­могою F-критерію Рішера, згідно з яким розрахункове зна­чення статистики

(2.20)

або

(2.21)

порівнюється з табличними F_т. Якщо розрахункове значен­ня F_ф, менше за табличне F_т(F_ф – F_т), то при заданому рівні значущості а гіпотеза про рівність двох дисперсій приймаєть­ся. У противному разі, коли розрахункове значення F_ф. більше за табличне F_т(F_ф – F_т), гіпотеза стосовно рівності дисперсій відхиляється. Тоді формула (2.18) для перевірки рівності се­редніх непридатна.

Наприклад, користуючись даними про виробництво цукру-піску сільськогосподарськими підприємствами Украї­ни*, визначимо наявність основної тенденції в середньому (табл.2.1)*

Таблиця 2.1