3.7. Метод експоненціального згладжування (метод Брауна)

Суть методу експоненціального згладжування, роз­робленого Р.Г.Брауном, полягає в тому, що часовий ряд ви­рівнюється з допомогою зваженої ковзної середньої, ваги якої підпорядковані експоненціальному закону. Зважена ковзна середня з експоненціальне розподіленими вагами характеризує значення процесу в кінці досліджуваного про­міжку, тобто є певною середньою характеристикою рівнів ряду. Саме ця властивість і використовується для прогнозу­вання динаміки. Виходячи з властивості існування інерції при моделюванні соціально-економічних процесів, внаслі­док якої вони відбуватимуться в період, що прогнозується гак само, як і в досліджуваному, зважену ковзну середню правомірно використовувати для прогнозування.

Нехай заданий часовий ряд опи­сується многочленом р-го порядку

де - коефіцієнти ряду; - випадкова вели­чина.

Необхідно при відомих рівнях ряду знайти його значення (п + l; l == 1, 2, ..., L) в момент часу t шляхом зваження спостережень так, щоб наступним спостережен­ням відповідали більші ваги, ніж попереднім.

Прогноз рівнів ряду , у момент часу (t + l; tt =n) будують, розкладаючи його в ряд Тейлора:

де - İ-та похідна в момент часу t.

Згідно з теоремою Брауна - Маєра довільна і-та по­хідна (İ= 0, 1, 2, ..., р) з рівняння (3.46) може бути виражена через лінійні комбінації експоненціальних середніх до (р + і)-го порядку. Отже, основною метою експоненціального зглад­жування є знаходження рекурентних уточнень оцінок ко­ефіцієнтів ряду (3.45).

Перш ніж виводити формули експоненціального зглад­жування, наведемо означення.

Експоненціальною середньою першого порядку для ряду у, називається вираз

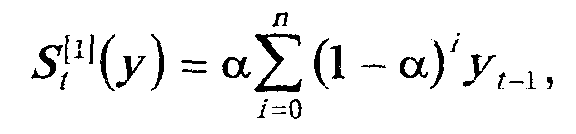
де а - параметр згладжування (0 < а < 1).

Експоненціальна середня к-го порядку для ряду має вигляд

Для обчислення експоненціальної середньої Браун отримав рекурентну формулу

Функція (3.49) є лінійною комбінацією всіх попередніх спостережень. Ваги, які відповідають минулим рівням, змен­шуються за геометричною прогресією.

Використовуючи рекуретну формулу (3.49), запише­мо рівняння для знаходження експоненціальних середніх:

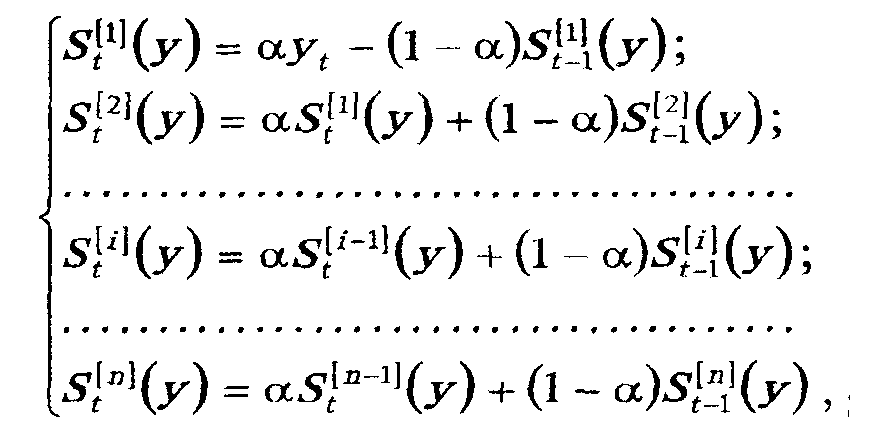
де (y) – експоненціальна İ -го порядку.

Покажемо тепер, як на основі системи (3.50) знахо­дяться коефіцієнти відповідних моделей. Нехай задана лінійна модель

Згідно з теоремою Брауна - Маєра дістаємо систему рівнянь для знаходження невідомих параметрів a_·0 і а₁ через експоненціальні середні і :

Звідси

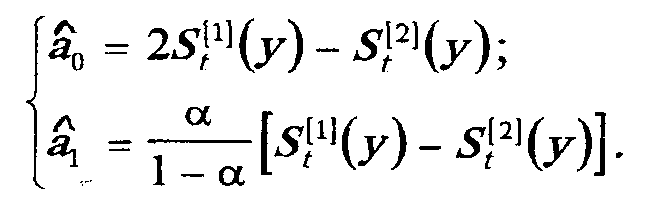
Запишемо вирази для знаходження експоненціальних середніх

і початкових умов

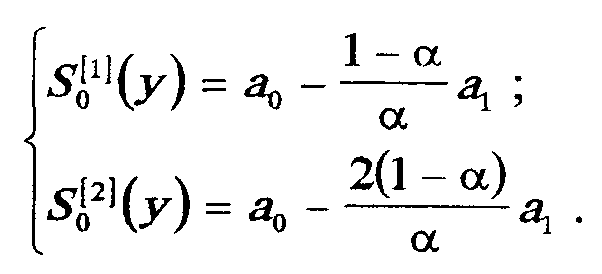
Прогноз для рівняння (3.51) знаходимо за формулою

де l - період прогнозу.

Похибка при лінійному прогнозуванні визначається за формулою

де - середньоквадратична похибка, обчислена для відхи­лень від лінійного тренду,

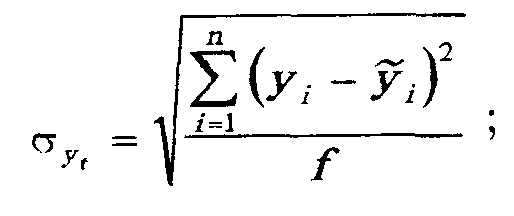
і - відповідно фактичні й теоре­тичні (знайдені на основі прогнозу) значення членів ряду; f-число ступенів свободи.

Якщо ряд динаміки описується параболою другого порядку

то основні показники експоненціального згладжування роз­раховуються за такими формулами:

1) початкові умови:

2) експоненціальні середні:

3) оцінки коефіцієнтів тренду

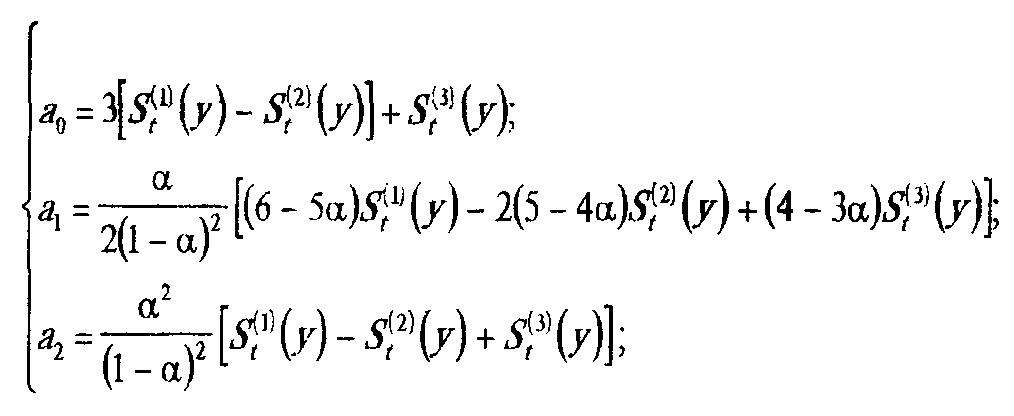
4) модель, за якою робиться прогноз,

5) похибка прогнозу

Оцінку параметрів а₀, а₁, а₂ найкраще знаходити мето­дом найменших квадратів.

У методі експоненціального згладжування важливим є вибір параметра згладжування а, оскільки при різних його значеннях прогнозні значення рівнів також різні. Якщо α наближається до одиниці, це свідчить про великий вплив на прогноз лише останніх спостережень; якщо а наближаєть­ся до нуля, то ваги рівнів зменшуються повільно, тобто при прогнозуванні враховуються всі (або майже всі) попередні спостереження.

Коли є впевненість, що початкові умови досить пра­вильні, параметр α беруть таким, що наближається до нуля;

у противному разі слід брати великі значення α. На прак­тиці для знаходження значень параметра згладжування ко­ристуються формулою

яка відображає залежність лише від загальної кількості рівнів ряду динаміки п.

Нарешті, слід звернути увагу на те, що метод експонен­ціального згладжування в основному забезпечує хороші ре­зультати при прогнозуванні часових рядів з великою кіль­кістю спостережень. Для коротких рядів динаміки він часто "не спрацьовує". Останнє пояснюється тим, що економічні часові ряди, як правило, досить короткі (15-20 спостере­жень), тому для невеликих значень темпів зростання і при­росту даний метод "не встигає" відобразити всі зміни. Крім того, точність прогнозу значною мірою залежить від почат­кових умов і параметра а.

Приклад 1. Використовуючи дані про урожайність со­няшника в Україні за 1966-1984 pp. (табл. 3.13), визначити методом експоненціального згладжування прогноз урожай­ності соняшника на 1985-1990 pp.

Тренд ряду динаміки врожайності соняшника, знай­дений за методом найменших квадратів, має вигляд

Параметр згладжування а при я = 19 набуває значення

Таблиця 3.13

Фактичні й теоретичні (розрахункові) значення врожайності соняшника в Україні

Рік	Значення рівня
	фактичне у	теоретичне
1	2	3	4	5
1966	15,8	16,79	-0,99	0,9801
1967	16,6	16,62	-0,02	0,0004
1968	15,8	16,45	-0,65	0,4225
1969	18,2	16,28	1,92	3,6864
1970	15,4	16,11	-0,71	0,5041
1971	15,8	15,94	-0,14	0,0196
1972	13,6	15,77	-2,17	4,7089
1973	18,1	15,60	2,50	6,2500
1974	17,3	15,43	1,87	3,4969
1975	14,1	15,26	- 1,16	1,3456
1976	12,3	15,09	-2,79	7,7841
1977	15,7	14,92	0,78	0,6084
1978	14,3	14,75	-0,45	0,2025
1979	16,0	14,58	1,42	2,0164
1980	13,4	14,41	- 1,01	1,0201
1981	14,2	14,24	- 0,04	0,0016
1982	15,6	14,07	1,53	2,3409
1983	13,7	13,90	-0,20	0,0400
1984	14,0	13,73	0,27	0,0729
Разом	289,9	289,94	0	35,5014

Початкові умови визначаємо за формулою (3.55):

Далі обчислюємо експоненціальні середні першого і другого порядків за формулою (3.54):

Звідси оцінки параметрів лінійного тренду

Отже, прогноз урожайності соняшника в Україні ро­биться згідно з моделлю

Похибки прогнозованих значень знайдемо за форму­лою (3.57). Після відповідних обчислень наведемо оцінки прогнозів урожайності соняшника на 1985-1990 pp. (табл. 3.14).

Таблиця 3.14