§ 48. Основные геодезические задачи

При производстве геодезических работ обычно приходится ре­шать прямую и обратную геодезические задачи.

Прямая геодезическая задача. Пусть на местности имеется пункт А (х_А, у_А) с известными координатами (рис. 64). Зная дирекционный угол α линии между пунктами А и В и горизонтальную проекцию длины этой линии d, можно вычислить координаты пункта В. Эта за­дача называется прямой геодезической задачей. Рассмотрим ее решение на плоскости. Спроецировав точки А и В на оси ко­ординат, из рис. 64 видим, что координаты х, у точки В равны координатам точки А плюс соответственно величины Δx и Δy, т. е.

x_B = x_A + Δx;

y_B = x_A + Δy. (48.1)

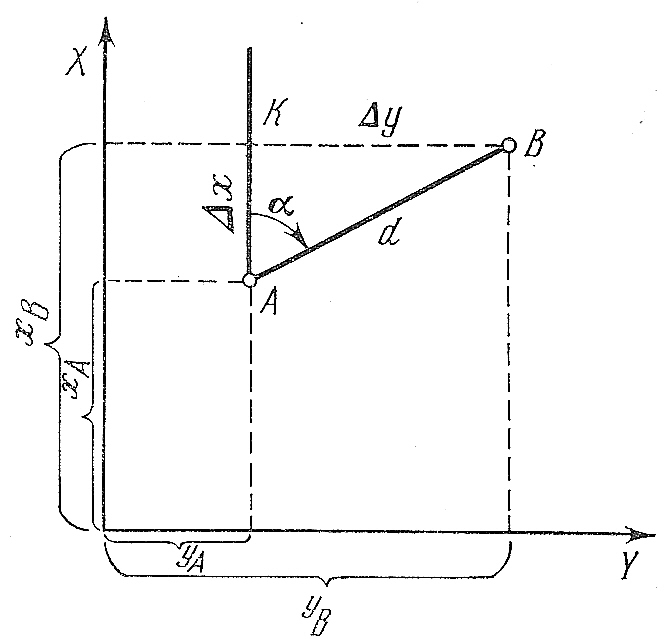
Рис. 64. Основные геодезические задачи

Отрезки Δх и Δу представляют собой проекции отрезка АВ на соответствующие оси координат и называются прираще­ниями координат. Приращения координат Δх и Δу опреде­ляем из прямоугольного треугольника АКВ по известным вели­чинам дирекционного угла α и длины d:

Δx = d cosα;

Δy = d sinα. (48.2)

Подставив значения приращений координат (48.2) в выражение (48.1), получим решение прямой геодезической задачи

x_B = x_A + d cosα;

y_B = y_A + d sinα. (48.3)

Решение прямых геодезических задач целесообразно выполнять с помощью микрокалькуляторов.

Применение микрокальку­ляторов не требует перехода от дирекционных углов к рум­бам, автоматизирует вычисли­тельный процесс, сокращает затраты времени и повышает надежность вычислений.

Обратная геодезическая задача Если на местности известны координаты двух точек А (х_А. у_А) и В (х_В, у_В), то можно определить горизонтальную проек­цию расстояния между этими пунктами d и дирекционный угол этого направления α (см. рис. 64). Эта задача носит название обратной геодезической задачи.

В обратной геодезической задаче, как видно из рис. 64, приращения координат могут быть вычислены по исходным дан­ным:

Δx = x_B – x_A;

Δy = y_B – y_A. (48.4)

Из прямоугольного треугольника АКВ можно определить угол α и горизонтальную проекцию расстояния

tg α = ; α = arctg ; d = . (48.5)

С помощью формул (48.5) решают обратную геодезическую задачу, при этом горизонтальную проекцию расстояния d для контроля вычисляют дважды. Если возникает необходимость определения только горизонтальной проекции расстояния между точками с известными координатами без определения направления, то пользуются формулой:

d = . (48.6)

Для решения обратной геодезической задачи, так же как и прямой, используются микрокалькуляторы. Назад