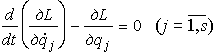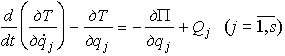- •Предмет и содержание динамики, основные понятия и определения. Законы Галилея-Ньютона.
- •Дифференциальные уравнения движения свободной и несвободной материальной точки в трех формах.
- •Две основные задачи динамики. Решение первой основной задачи динамики точки.
- •Основное уравнение относительного движения. Переносная и кориолисова силы инерции.
- •Принцип относительности классической механики. Инерциальные системы отсчета. Случай относительного покоя.
- •Свободные колебания материальной точки. Дифференциальное уравнение движения, его решение, частота и период свободных колебаний.
- •Влияние сил сопротивления, пропорциональных скорости точки, на свободные колебания (затухающие колебания). Декремент и логарифмический декремент колебаний.
- •Где − период свободных колебаний без сопротивления. Если , то сопротивление практически не влияет на период колебаний .
- •Вынужденные колебания при гармонической возмущающей силе без учета сил сопротивления. Амплитуда вынужденных колебаний. Коэффициент динамичности. Явление резонанса. Явление биений.
- •Механическая система, масса, центр масс и его координаты.
- •Осевые моменты инерции точки и системы. Радиус инерции. Моменты инерции простейших тел.
- •Теорема о моментах инерции относительно параллельных осей (теорема Гюйгенса - Штейнера).
- •Внешние и внутренние силы. Свойства внутренних сил.
- •Дифференциальные уравнения движения механической системы.
- •Теорема о движении центра масс. Следствия.
- •Количество движения материальной точки и механической системы. Элементарный и полный импульс силы.
- •Теорема об изменении количества движения точки и системы в дифференциальной и интегральной формах. Следствия.
- •Момент количества движения точки и системы относительно центра и оси. Кинетический момент вращающегося твердого тела.
- •Теорема об изменении кинетического момента точки и системы относительно центра и оси. Законы сохранения.
- •1. Если главный вектор всех внешних сил системы равен нулю ( ), то количество движения системы постоянно по величине и направлению.
- •2. Если проекция главного вектора всех внешних сил системы на какую-либо ось равна нулю ( ), то проекция количества движения системы на эту ось является постоянной величиной.
- •Элементарная и полная работа силы. Мощность силы.
- •Работа и мощность силы, приложенной к твердому телу, вращающемуся вокруг неподвижной оси.
- •Работа силы тяжести, силы упругости. Работа внутренних сил неизменяемой системы.
- •Кинетическая энергия точки и системы. Кинетическая энергия тела при поступательном, вращательном и плоскопараллельном движениях.
- •Теорема об изменении кинетической энергии точки и системы в трех формах.
- •Дифференциальные уравнения поступательного, вращательного и плоско - параллельного движений твердого тела.
- •Силовое поле. Потенциал силового поля. Силовая функция и потенциальная энергия. Эквипотенциальные поверхности. Закон сохранения механической энергии.
- •Связи, их уравнения и классификация.
- •Действительное и возможное перемещение. Возможная работа. Идеальные связи.
- •Принцип возможных перемещений.
- •Применение принципа возможных перемещений к определению реакций связей составных конструкций.
- •Сила инерции материальной точки. Главный вектор и главный момент сил инерции при различных случаях движения твердого тела.
- •5.2.1. Сила инерции материальной точки
- •5.2.2. Силы инерции в поступательном движении твердого тела
- •5.2.3. Силы инерции во вращательном движении твердого тела, имеющего плоскость материальной симметрии
- •Принцип Даламбера для точки системы. Метод кинетостатики.
- •Общее уравнение динамики.
- •Обобщенные координаты. Обобщенные силы и их вычисление. Случай потенциальных сил.
- •Уравнения равновесия и движения в обобщенных координатах.
- •Виды равновесия. Понятие об устойчивости равновесия.
- •Теорема Лагранжа-Дирихле.
- •Дифференциальные уравнения движения механической системы в обобщенных координатах или уравнения Лагранжа второго рода (без вывода).
- •Уравнения Лагранжа 2 рода для консервативных систем. Кинетический потенциал.
- •Этот результат получается проектированием предыдущего равенства на ось .
- •Удар точки о неподвижную поверхность. Коэффициент восстановления.
- •Для определения ударного импульса запишем теорему об изменении количества движения за время удара для одного из тел в проекции на направление движения . Откуда
- •При абсолютно упругом ударе ударный импульс в два раза больше, чем при абсолютно неупругом.
- •Прямой центральный удар двух тел. Теорема Карно.
Уравнения Лагранжа 2 рода для консервативных систем. Кинетический потенциал.
Если все силы системы потенциальны, то обобщенные силы системы выражаются через потенциальную энергию системы как Qj = -дП / дqj, а уравнения Лагранжа второго рода запишутся в виде
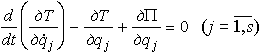
Так как потенциальная энергия не зависит от обобщенных скоростей, то . Введем в рассмотрение функцию
L = T - П |
(4) |
которую называют функцией Лагранжа или кинетическим потенциалом. Тогда уравнения Лагранжа в случае потенциальных сил запишутся так:
|
(5) |
Если среди сил системы вместе с потенциальными присутствуют непотенциальные силы, например силы трения, то обобщенные силы системы складываются из обобщенных потенциальных сил Qjn = -дП / дqj и обобщенных непотенциальных сил Qj, а уравнения (3) принимают вид
|
(6) |
Явление удара. Ударная сила и ударный импульс. Основная теорема удара. Свойства удара.
Ударом будем называть кратковременное действие на тело некоторой силы . Силы, возникающей, например, при встрече двух массивных тел.
Опыт показывает, что взаимодействие их очень кратковременно (время контакта исчисляется тысячными долями секунды), а сила удара довольно велика (в сотни раз превышает вес этих тел). Да и сама сила – не постоянна по величине. Поэтому явление удара - сложный процесс, сопровождающийся к тому же деформацией тел. Точное исследование его требует знания физики твердого тела, законов тепловых процессов, теории упругости и др.
Мы же воспользуемся довольно простыми методами исследования, но которые, как подтверждает практика, достаточно правильно объясняют явление удара.
Поскольку
сила удара
очень
велика, а продолжительность его, время
,
мало, при описании процесса удара будем
пользоваться не дифференциальными
уравнениями движения, а теоремой об
изменении количества движения. Потому
что измеряемой конечной величиной
является не сила удара, а импульс ее
![]()
Чтобы сформулировать первые особенности явления удара, рассмотрим сначала действие такой силы на материальную точку.
Пусть
к материальной точке М,
движущейся под действием обычных сил
![]() по некоторой траектории (рис.111), в
какой-то момент была приложена мгновенная,
большая сила
.
С помощью теоремы об изменении количества
движения за время удара
составляем уравнение
по некоторой траектории (рис.111), в
какой-то момент была приложена мгновенная,
большая сила
.
С помощью теоремы об изменении количества
движения за время удара
составляем уравнение
![]() где
где
![]() и
и
![]() - скорости точки в конце и в начале удара;
- скорости точки в конце и в начале удара;
![]() - импульс мгновенной силы
.
Импульсами обычных сил, под действием
которых точка двигалась, можно пренебречь
– за время τ
они будут очень малы.
- импульс мгновенной силы
.
Импульсами обычных сил, под действием
которых точка двигалась, можно пренебречь
– за время τ
они будут очень малы.
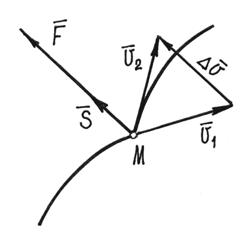
Рис.111
Из уравнения находим изменение скорости за время удара (рис.111):
![]() .
.
Это изменение скорости оказывается конечной величиной.
Дальнейшее движение точки начнется со скоростью и продолжится под действием прежних сил, но по траектории, получившей излом.
Теперь можно сделать несколько выводов.
1. При исследовании явления удара обычные силы можно не учитывать.
2. Так как время τ мало, перемещением точки за время удара можно пренебречь.
3. Единственный результат действия удара – только изменение вектора скорости.
Теорема об изменении количества движения механической системы при ударе.
Изменение количества движения механической системы за время удара равно сумме внешних ударных импульсов, действующих на точки системы.
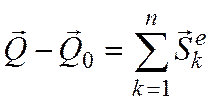
Доказательство. Разделим ударные силы, действующие на каждую точку механической системы, на внешние и внутренние. Запишем основное уравнение удара для каждой точки системы
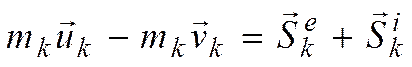 ,
,
![]() ,
,
где
![]() ,
,
![]()
равнодействующие внешних и внутренних
ударных импульсов. Суммируя полученные
равенства, с учетом свойства внутренних
сил находим:
равнодействующие внешних и внутренних
ударных импульсов. Суммируя полученные
равенства, с учетом свойства внутренних
сил находим:
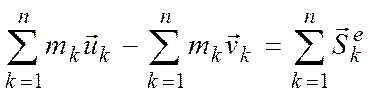 .
.
Следствие. При действии на механическую систему лишь внутренних ударных импульсов количество движения системы не изменяется.
Теорема об изменении кинетического момента механической системы при ударе. Изменение кинетического момента механической системы относительно любого неподвижного центра за время удара равно сумме моментов всех внешних ударных импульсов, приложенных к точкам системы, относительно этого же центра.
 .
.
Основное
уравнение удара для каждой точки системы
![]() ,
,
![]() .
Так как положение точек системы за
время удара не изменяется, то умножая
на радиус-вектор
.
Так как положение точек системы за
время удара не изменяется, то умножая
на радиус-вектор
![]() -ой
точки
-ой
точки
![]() (рис. 18.1), можно записать
(рис. 18.1), можно записать
![]() ,
,
![]() .
.
Суммируя полученные равенства,
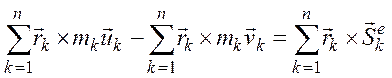
![]()
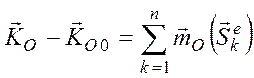 .
.


Следствие. Внутренние ударные импульсы не влияют на изменение кинетического момента системы.
Теорема об изменении кинетического момента в скалярной форме. Изменение кинетического момента механической системы относительно неподвижной оси за время удара равно сумме моментов всех внешних ударных импульсов, приложенных к точкам системы, относительно той же оси.
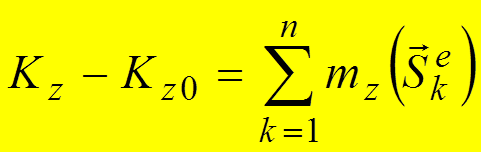 .
.