1 Проецирование центральное

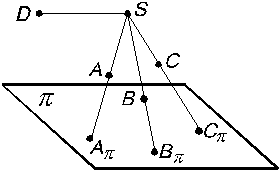
Центральным называется проецирование, при котором все проецирующие лучи выходят из одной точки S, называемой центром проецирования. На рисунке 1 дан пример центрального проецирования, где  – плоскость проекций; S – центр проецирования (точка, не лежащая в плоскости  ); А, В, С – точки пространства; А , В , С – центральные проекции точек А, В, С, на плоскость  : они получаются в пересечении проецирующих лучей SA, SB, SC c плоскостью проекций.

Если для некоторой точки D проецирующий луч окажется параллельным плоскости проекций, то принято считать, что они пересекаются, но в бесконечно удаленной точке. Проекцией точки D будет бесконечно удаленная точка D .

Проекции точек (А и В), лежащих на одном проецирующем луче, совпадают (А В ) (рис. 2).

Рисунок 1	Рисунок 2

Построение центральных проекций прямой линии АВ и кривой MN показано на (рис. 3 и 4).

Рисунок 3	Рисунок 4

 

2 Проецирование параллельное

Параллельным называется проецирование, при котором все проецирующие лучи между собой параллельны.

Параллельные проекции могут быть косоугольными (рис.1) и прямоугольными (рис. 2).

Рисунок 1	Рисунок 2

S – направление проецирования.

При косоугольном проецировании проецирующие лучи составляют с плоскостью проекций угол, не равный 90° .

При прямоугольном проецировании проецирующие лучи перпендикулярны плоскости проекций (прямоугольное проецирование чаще всего называют ортогональным проецированием).

Каждый из рассматриваемых способов имеет свои преимущества и недостатки. В зависимости от того, для какой цели выполняется чертеж, используется тот или иной способ.

Для выполнения чертежа, по которому изготовляется изображаемый предмет, используется ортогональное проецирование.

Косоугольное, параллельное проецирование используется в основном для получения аксонометрических изображений, центральное – для построения перспективных изображений.

В изучаемом курсе основное внимание будет уделено ортогональному проецированию.

3 Свойства ортогональных проекций

1. Проекция точки есть точка (рис. 1).

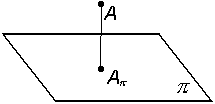
Рисунок 1

2. Проекция прямой в общем случае есть прямая (рис. 2).

Если прямая располагается перпендикулярно какой-либо плоскости проекций (такая прямая называется проецирующей), то на эту плоскость она проецируется в виде точки (рис. 2).

3. Если точка лежит на прямой, то ее проекция располагается на соответствующей проекции этой же прямой А m А_ m_ (рис. 3).

Рисунок 2	Рисунок 3

Примечание. Первые 3 свойства проекций являются общими для центрального и параллельного проецирования.

4. Если точка делит отрезок прямой в каком-либо отношении, то ее проекция делит проекцию отрезка в том же самом отношении (рис. 4).

В

Рисунок 4

5. Если прямая (плоская фигура) параллельна плоскости проекций, то на эту плоскость эта прямая проецируется без искажений (рис.5).

m II  m_ = m,              m II  [ А_ В_ ] = [ AB ].

6. Если прямые в пространстве пересекаются, то их проекции также пересекаются (рис. 6).

m n = C m_ п_ ⁼с_

Рисунок 5	Рисунок 6

7. Если прямые в пространстве параллельны, то их проекции также параллельны (рис. 7).

a II b а_ II b_

Примечание. Общими для косоугольного и прямоугольного проецирования являются свойства 4, 5, 6.

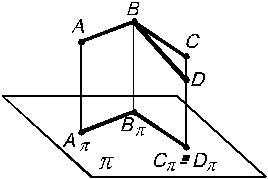
8. Если одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость прямой угол проецируется без искажений (рис. 8).

ABC = 90° ; AB||  ; BC||  ; А_ В_ С_ = 90° ;

ABD = 90° ; AB||  ; BD  ; А_ В_ D_ = 90° .

Рисунок 7	Рисунок 8

Примечание. Свойство 8-е только для ортогонального проецирования.

9. Параллельный перенос фигуры в пространстве или плоскости проекций не изменяет вида и размеров проекции фигуры.