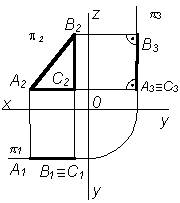- •Геометрические образы
- •Обозначение отношений между геометрическими образами
- •Обозначения теоретико-множественные
- •Метод проецирования
- •В иды проецирования
- •1 Проецирование центральное
- •2 Проецирование параллельное
- •3 Свойства ортогональных проекций
- •4 Обратимость чертежа. Метод Монжа
- •5 Система двух взаимно перпендикулярных плоскостей
- •6 Точка в системе двух плоскостей проекций 1 и 2
- •7 Образование комплексного чертежа (эпюра)
- •Пример изображения точек, принадлежащих плоскостям 1 и 2
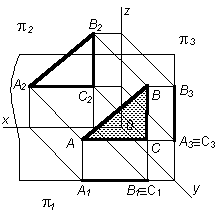
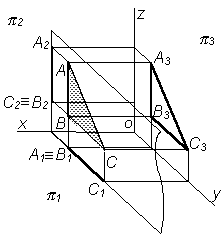
- •8 Система трех взаимно перпендикулярных плоскостей
- •9 Прямая линия. Задание прямой. Общие положения
- •9.1 Прямые частного положения
- •10 Плоскость Общие положения
- •Способы задания плоскости
- •Плоскости уровня
- •10.2 Прямые особого положения в плоскости
- •10.3 Принадлежность точки плоскости
- •11 Многогранники
- •11.1 Пересечение многогранника плоскостью
- •Пример построения сечений многогранников проецирующими плоскостями
- •11.2 Пересечение прямой с многогранной поверхностью
- •12 Преобразование комплексного чертежа
- •Вращение прямой линии
- •13 Кривые линии
- •Цилиндрическая винтовая линия
- •Коническая винтовая линия
- •14 Поверхности Образование поверхностей
- •14.1 Поверхности вращения
- •14.2 Линейчатые поверхности
- •14.3 Винтовые поверхности
- •14. 4 Циклические поверхности
- •15 Построение разверток поверхностей
- •15.1 Развертка поверхностей многогранника
- •15.2 Построение условной развертки
- •16 Касательные линии и плоскости к поверхности
- •17 Аксонометрические проекции
- •17.1 Прямоугольная изометрическая проекция
- •17.2 Прямоугольная диметрическая проекция
- •17.3 Косоугольные аксонометрические проекции
- •Фронтальная диметрическая проекция
- •Фронтальная изометрическая проекция
- •Горизонтальная изометрическая проекция
Плоскости уровня
Характеристика |
Наглядное изображение |
Эпюр |
Фронтальная плоскость – это плоскость, параллельная плоскости 2. Эта плоскость пересекает плоскость 1 параллельно оси ОХ, а плоскость 3 – по линии, параллельной оси OZ |
|
|
Горизонтальная плоскость – это плоскость, параллельная плоскости проекции 1. Эта плоскость пересекает плоскость 2 параллельно оси ОХ, а плоскость 3 – параллельно оси ОУ |
|
|
Профильная плоскость – это плоскость, параллельная плоскости 3. Эта плоскость пересекает плоскости проекций 1 и 2 по линиям, параллельным оси Z |
|
|
Таким образом, если плоскость параллельна какой-либо плоскости проекций, то на эту плоскость она проецируется в натуральную величину, а две ее другие проекции есть прямые линии параллельные осям проекций.
10.2 Прямые особого положения в плоскости
Прямыми особого положения в плоскости являются горизонталь h, фронталь f и линии наибольшего наклона к плоскостям проекций. Рассмотрим графическое изображение этих линий (табл. 4).
Таблица 4
Определение |
Комплексный чертеж |
1. Горизонталью плоскости называется прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций, обозначаемая h. Построение горизонтали начинается с фронтальной проекции h2. Все горизонтали одной плоскости между собой параллельны. Горизонталь есть геометрическое место точек плоскости, удаленных от плоскости 1 на одно и то же расстояние |
|
2. Фронталью плоскости называется прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций, обозначаемая f. Все фронтали одной плоскости параллельны между собой. Фронталь плоскости – это геометрическое место точек, удаленных от плоскости 2 на одно и то же расстояние |
|
3. Линиями наибольшего наклона данной плоскости к плоскостям проекций называются линии, лежащие в плоскости и перпендикулярные горизонтали, фронтали или ее профильной прямой. В первом случае определяется наклон данной плоскости к плоскости 1, во втором – к 2, в третьем – к 3. Линия наибольшего наклона к 1 называется линией наибольшего ската (ЛНС). Построение ЛНС начинается с ее горизонтальной проекции n1, так как согласно свойству проецирования прямого угла, угол 900 между ЛНС и h1 на 1 проецируется без искажения |
|
10.3 Принадлежность точки плоскости
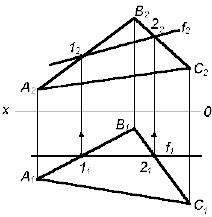
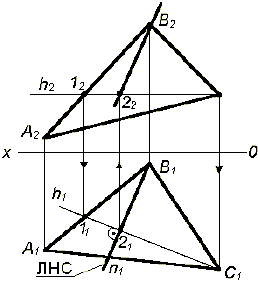
Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (рис.1).
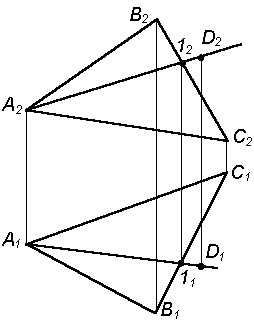
Рисунок 1
Точка D принадлежит плоскости ( АВС), так как D1 А111; D2 А212, а прямая А1 принадлежит плоскости ( АВС).
11 Многогранники
Многогранники – замкнутые пространственные фигуры, ограниченные плоскими многоугольниками. Вершины и ребра многогранников образуют пространственную сетку. Если вершины и ребра многогранника находятся по одну сторону плоскости любой из его граней, то многогранник называют выпуклым. Из всего многообразия многогранников наибольший практический интерес представляют призмы, пирамиды, правильные многогранники и их разновидности.
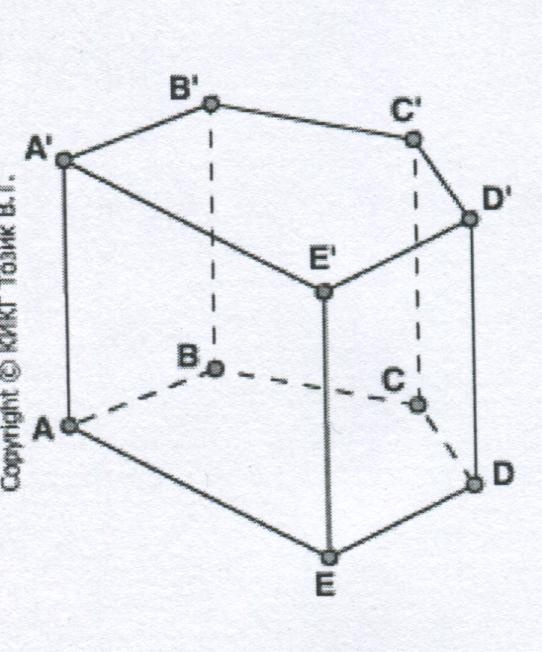
Рисунок 1
Многогранник, две грани которого n-угольники в параллельных плоскостях, а остальные n-граней - параллелограммы, называется n-угольной призмой (рис.1). Многогранники являются основаниями призмы, а параллелограммы – боковыми гранями призмы.
 Рисунок
2
Рисунок
2
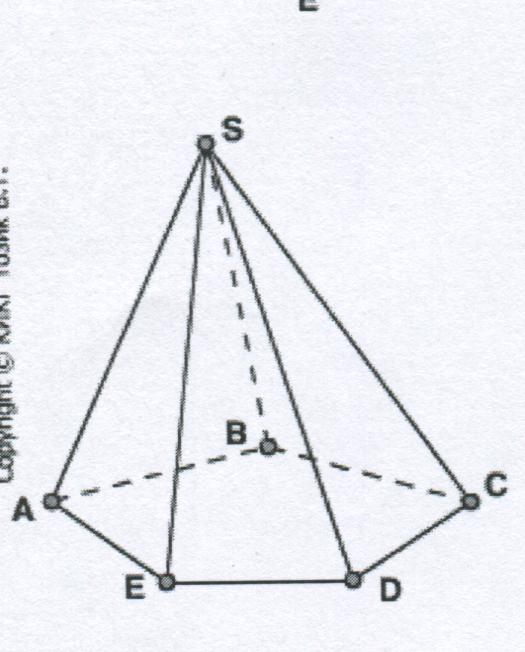
Многогранник, у которого одна из граней – произвольный многоугольник, а остальные грани – треугольники, имеющие общую (особую) вершину, называются пирамидой (рис.2). Грань–многоугольник называют основанием призмы, а треугольники – боковыми гранями пирамиды.
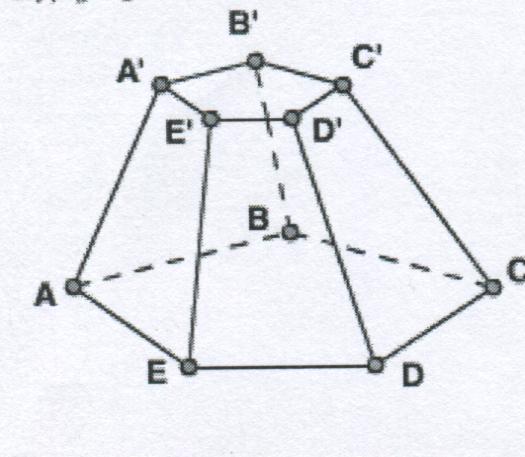
Рисунок 3
Если пирамиду отсечь плоскостью параллельной основанию, то получим усеченную пирамиду (рис.3).

Рисунок 4
Многогранник называется метрически правильным, если все его грани являются правильными многоугольниками. К ним относятся куб, тетраэдр, октаэдр, икосаэдр, додекаэдр (рис.4).
Под изображением многогранников на чертеже будем понимать изображение ограничивающей его многогранной поверхности, т.е. изображение совокупности составляющих ее многогранников. Графически простую многогранную поверхность удобно задавать проекциями ее сетки.
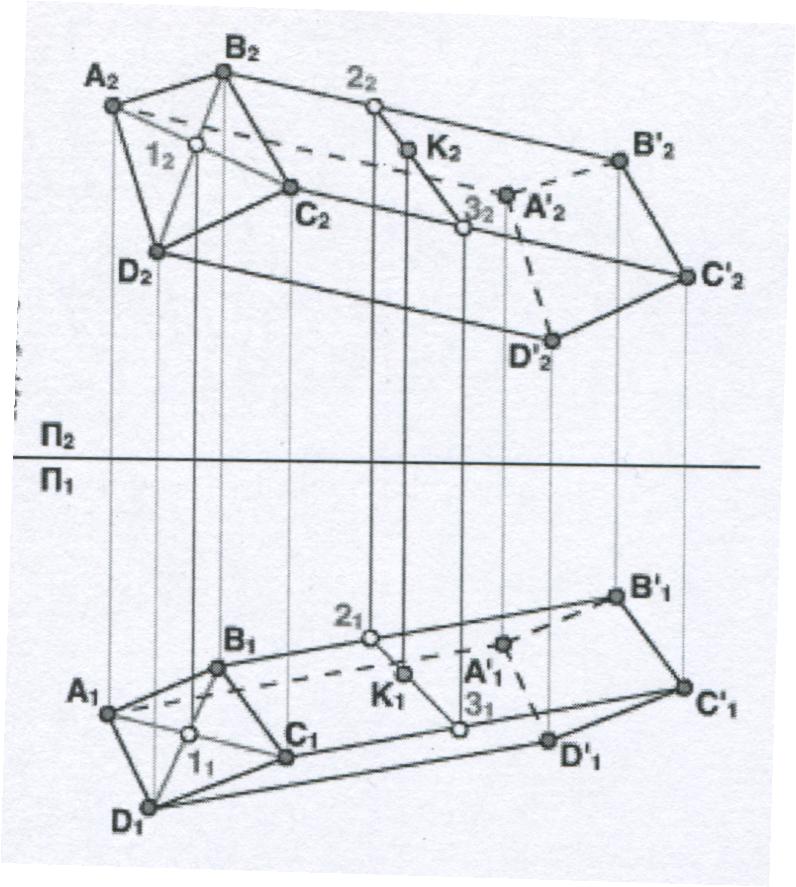
Рисунок 5
На рисунке многогранник АВСDА'В'С'D' задан проекциями его ребер и вершин (сетки), где А1А'1 | | В1В'1 | | С1С'1 | | D1D'1 и А2А'2 | | В2В'2 | | С2С'2 | | D2D'2. Значит ребра многогранника параллельны. Параллельны соответственные стороны многоугольника АВСD и А'В'С'D'. Грани АВВ'А', ВС С'B', СDD'C' и ADD'A' являются параллелограммами. Отсюда следует, что на чертеже задана призма. Четырехугольник ABCD плоский, т. к. его диагонали пересекаются в точке 1.
На этом же чертеже показано построение горизонтальной проекции K1 точки K по заданной ее фронтальной проекции K2 из условия принадлежности точки K грани BB'C'C. Горизонтальная проекция точки K построена с помощью вспомогательной прямой 23, проведенной через точку K в плоскости BB'C'C.
Такой чертеж многогранной поверхности АВСDА'В'С'D', когда можно построить проекцию любой точки, принадлежащей многогранной поверхности называется полным.