14. 4 Циклические поверхности

Циклической поверхностью называется поверхность, которая описывается какой-либо окружностью (образующей) постоянного или переменного радиуса при ее произвольном движении.

Из рассмотренных выше поверхностей к циклическим можно отнести все поверхности вращения. Кроме этого, к циклическим поверхностям можно отнести каналовые и трубчатые поверхности.

Каналовая поверхность образуется движением окружности переменного радиуса, причем центр окружности О перемещается по заданной кривой l (направляющей), а ее плоскость остается перпендикулярной к этой кривой (рис. 6).

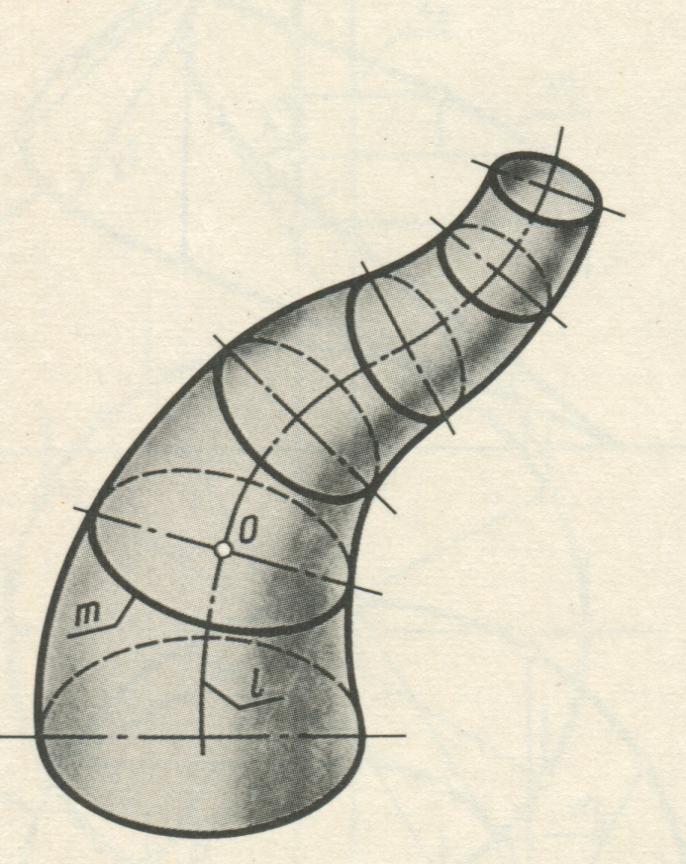
Рисунок 6

Трубчатая поверхность отличается от каналовой только тем, что ее образующая окружность m имеет постоянный радиус (рис. 7).

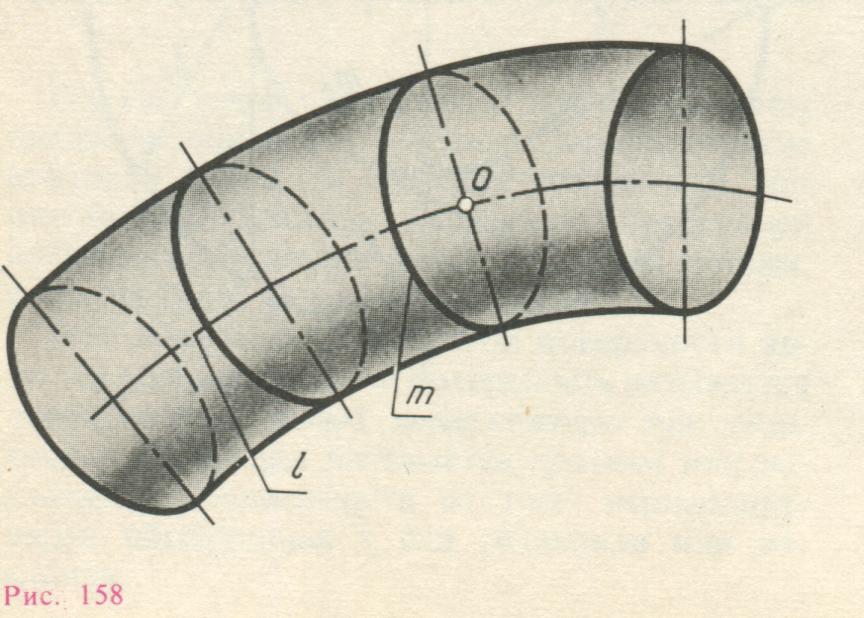
Рисунок 7

15 Построение разверток поверхностей

При построении разверток поверхностей последние рассматривают, как гибкие, нерастяжимые пленки. Развертка поверхности есть результат последовательного совмещения с плоскостью бесконечно малых элементов поверхности.

Если рассматриваемая поверхность может быть совмещена с плоскостью без складок и разрывов, то она называется развертывающейся (точной), если нет, то такая поверхность относится к неразвертываемой (приближенной).

Точные развертки имеют все многогранники (призмы, пирамиды и др.), цилиндрические и конические поверхности и некоторые другие. Приближенные развертки имеют шар, и другие поверхности вращения с криволинейной образующей.

Поверхность называется развертывающейся на плоскость , если между их точками и (рис.1) можно установить взаимно однозначное соответствие, при котором сохраняются длины линий, расположенных на поверхности, величины углов между линиями и площади фигур, ограниченных замкнутыми линиями.

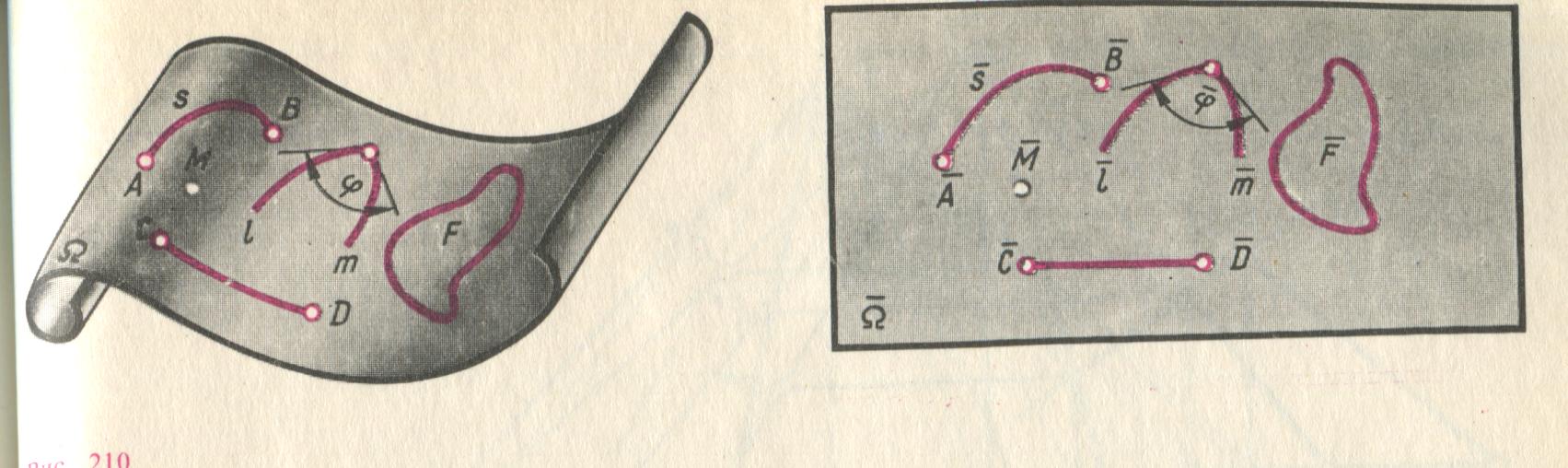
Рисунок 1

Основные свойства развертки:

1. длины двух соответствующих линий поверхности и ее развертки равны между собой;

2. угол между линиями на поверхности равен углу между соответствующими им линиями на развертке;

3. прямой на поверхности соответствует также прямая на развертке;

4. параллельным прямым на поверхности соответствуют также параллельные прямые на развертке;

5. если линии, принадлежащей поверхности и соединяющей две точки поверхности, соответствует прямая на развертке, то эта линия является геодезической.

15.1 Развертка поверхностей многогранника

Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, построение ее сводится к определению величины отдельных граней поверхности – плоских многоугольников.

Существует три метода построения развертки многогранных поверхностей:

1. Метод треугольника (триангуляции).

2. Метод нормального сечения.

3. Метод раскатки.

1. Метод треугольника

.

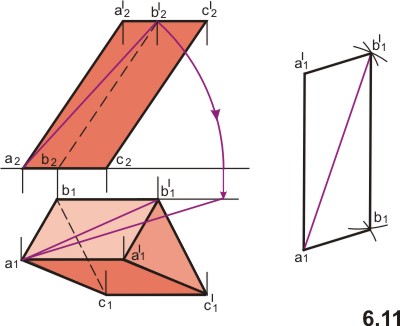
Рисунок 2

Сущность способа треугольников (рис 2) состоит в том, что каждая грань призмы разбивается диагональю на два треугольника, затем определяются истинные величины всех сторон треугольников, которые последовательно вычерчиваются в истинную величину на свободном поле чертежа. На рисунке 2 этот способ применен для построения развертки боковой поверхности трехгранной наклонной призмы. Грань a₁b₁b′₁a′₁ диагональю а₁b′₁ разделена на два треугольника. Для построения истинной величины треугольника a₁a′₁b′₁ надо определить истинную величину только одной его стороны - стороны а₁b′₁, так как в приведенном примере две другие стороны этого треугольника расположены относительно плоскостей проекций так, что одна из их проекций является истинной величиной: истинная величина стороны а′₁b′₁ - ее горизонтальная проекция a′₁b′₁, стороны а₁b′₁ - фронтальная a₂a′₂. Истинная величина стороны a₁b′₁ определена вращением ее вокруг оси перпендикулярной к плоскости проекций П₂ и проходящей через точку а₁.

2. Метод нормального сечения

На рисунке 3 развертка боковой поверхности трехгранной наклонной призмы построена способом нормального сечения. Последовательность:

1. призма рассекается перпендикулярной к ее ребрам или граням плоскостью. Фронтально проецирующая плоскость Р₂ горизонтально след которой на эпюре не показан;

2. строится проекция и определяется истинная величина фигуры нормального сечения. На риуснке 3 фронтальная проекция фигуры сечения (1-2-3) совпадает со следом секущей плоскости, а горизонтальная не показана. Истинная величина фигуры сечения (1₀-2₀-3₀) построена способом совмещения - плоскость Р вращением вокруг ее горизонтального следа совмещена с плоскостью проекции П₁;

3. истинная величина фигуры нормального сечения на свободном поле чертежа разворачиваеться в прямую линию (1₀-1₀) и от точек 1₀, 2₀, 3₀, 1₀ проводятся перпендикуляры к прямой 1₀-1₀;

4. На перпендикулярах по обе стороны от точек 1₀, 2₀, 3₀, 1₀ откладываются истинные величины соответствующих ребер призмы и полученные точки a₁, b₁, c₁, a₁ и a′₁, b′₁, c′₁, a′₁ соединяются отрезками прямых. В рассматриваемом примере ребра призмы параллельны плоскости проекции П₂, а следовательно истинными величинами их являются соответствующие фронтальные проекции.

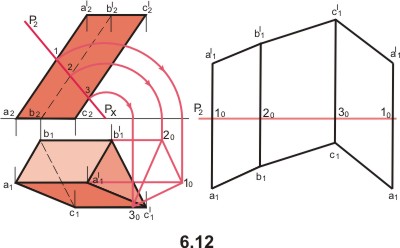
Рисунок 3

3. Метод раскатки

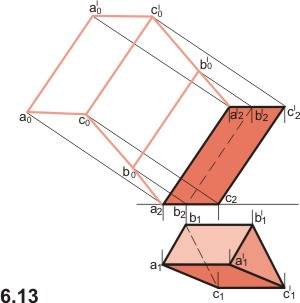
Рисунок 4

Способ раскатки применим тогда, когда ребра призмы параллельны одной из плоскостей проекции, например, плоскости проекции П₂ на рисунке 6.13. При этих условиях каждую грань призмы последовательно поворачивают вокруг одного из ребер, как вокруг фронтали, до положения, параллельного плоскости проекции П₂; все грани призмы спроецируются на плоскость проекции П₂ в натуральную величину. Построение: из фронтальных проекций точек a₂, b₂, c₂, a′₂, b′₂, c′₂ проводят перпендикуляры к ребрам призмы.

В рассматриваемом примере раскатка боковой поверхности призмы начата с грани a₂b₂b′₂a′₂. Чтобы повернуть ее вокруг ребра AA′ до положения, параллельного плоскости проекций П₂, из точек a₂ и a′₂ на перпендикулярах, выходящих из точек b₂ и b′₂, сделаны засечки раствором циркуля, равным истинной величине стороны AB (A′B′) основания призмы (истинной величиной стороны AB основания призмы является ее горизонтальная проекция a₁b₁). Параллелограмм a₂b₀b′₀a′₂ есть истинная величина грани ABB′A′. Истинная величина граней BB′C′C, CC′A′A построена аналогично. Фигура a₂b₀c₀a₀a′₀c′₀b′₀a′₂ - развертка боковой поверхности призмы.

Во всех рассмотренных примерах ребра призмы занимали частное положения относительно плоскостей проекций - они были параллельны плоскости проекций П₂, а основания призмы - плоскости проекции П₁. При построении разверток поверхности призмы, ребра которых занимают общие положения относительно плоскостей проекции, целесообразно вначале, применив способ замены плоскостей проекций, преобразовать эпюр так чтобы ребра призмы заняли частные положения, затем выполнить построение, аналогичное одному из описанных выше способов.