Глава 3. Структуры данных для задач, касающихся работы с множествами

Хороший подход к разработке эффективного алгоритма для данной задачи – изучить ее сущность. Часто задачу можно сформулировать на языке основных математических понятий, таких, как множество, и тогда алгоритм для нее можно изложить в терминах основных операций над основными объектами. Преимущество такой точки зрения в том, что можно проанализировать несколько различных структур данных и выбрать из них ту, которая лучше всего подходит для задачи в целом. Таким образом, разработка хорошей структуры данных идет рука об руку с разработкой хорошего алгоритма.

В настоящей главе изучаются семь основных операций над множествами, типичных для многих задач информационного поиска. Приводятся разнообразные структуры данных для представления множеств и рассматривается пригодность каждой из них в ситуациях, когда выполняется та или иная последовательность операций различных типов.

3.1. Основные операции над множествами

Будем рассматривать, следующие основные операции над множествами.

1. ПРИНАДЛЕЖАТЬ – Member(a, S). Устанавливает принадлежность а множеству S; если а  S, результат операции – "да"; в противном случае – "нет."

2. ВСТАВИТЬ – Insert(a, S). Заменяет S на S{a}.

3. УДАЛИТЬ – Delete(a, S). Заменяет S на S–{a}.

4. ОБЪЕДИНИТЬ – Union(S₁, S₂, S₃). Строит множество S₃=S₁S₂. Предполагается, что в тех случаях, когда применяется эта операция, множества S₁ и S₂ не пересекаются; это делается для того, чтобы избежать необходимости удалять повторяющиеся экземпляры одного и того же элемента в S₁S₂.

5. НАЙТИ – Find(а). Печатает имя того множества, которому в данный момент принадлежит а. Если а принадлежит более чем одному множеству, то операция не определена.

6. РАСЦЕПИТЬ – Split(а, S). Здесь предполагается, что множество S наделено линейным порядком . Операция разбивает S на два множества S₁={b|ba и bS} и S₂={b|b>a и bS}.

7. MIN(S). Выдает наименьший (относительно ) элемент множества S.

Многие задачи, встречающиеся на практике, можно свести к одной или нескольким подзадачам, таким, что каждую подзадачу можно абстрактно сформулировать как последовательность основных команд, которые следует выполнить на некоторой базе данных (универсальном множестве элементов). В данной главе будут изучаться последовательности  команд, каждая из которых является операцией одного из перечисленных выше семи типов.

Например, выполнение последовательностей, состоящих из операций ПРИНАДЛЕ­ЖАТЬ, ВСТАВИТЬ и УДАЛИТЬ, составляет существенную часть многих задач поиска. Структура данных, которую можно использовать для выполнения последовательности этих операций, будет называться словарем (dictionary). В настоящей главе рассматривается несколько структур данных (такие, как таблицы расстановки, деревья двоичного поиска и 2-3-деревья), которые могут быть словарями.

Здесь возникает много интересных вопросов. Прежде всего, интерес представляет временная сложность выполнения операций в , т. е. время как функция длины последовательности а и размера базы данных. Временная сложность исследуется в худшем случае и в среднем, а также исследуется сложность выполнения о в префиксном и свободном режимах.

Определение. Выполнение последовательности операций  в префиксном режиме (on-line) требует, чтобы операции в о выполнялись в порядке слева направо, причем i-я операция в  должна выполняться без просмотра какой бы то ни было последующей операции. При свободном режиме (off-line) разрешается просматривать всю последовательность а в любой момент времени.

Очевидно, что всякий префиксный алгоритм (т. е. работающий в префиксном режиме) может работать как свободный (т. е. в свободном режиме), но обратное верно не всегда. Бывают ситуации, когда свободный алгоритм работает быстрее любого из известных префиксных. Однако во многих приложениях приходится рассматривать только префиксные алгоритмы.

Пусть дана последовательность операций, которую надлежит выполнить. Основной вопрос: какую структуру данных использовать для представления универсальной базы данных? Часто задача будет требовать осторожного взвешивания всех за и против каждого конкретного выбора. В типичной ситуации последовательность будет состоять из нескольких операций, подлежащих многократному выполнению, часто в неизвестном порядке. Может оказаться несколько структур данных, каждая из которых позволяет одну операцию выполнять легко, а другие – с большим трудом. Во многих случаях лучшим решением будет компромисс. Часто мы будем использовать структуру, которая не делает максимально легким выполнение ни одной из операций, но позволяет выполнить всю работу лучше, чем при любом очевидном подходе.

3.2. Метод расстановки

Кроме вопроса о том, какие операции появляются в данной последовательности , возникает еще один важный вопрос, связанный с выбором подходящей структуры данных для выполнения . Это вопрос о размере базы данных (универсального множества), на которой работают операции из . Например, в гл. 2 было показано, что с помощью сортировки вычерпыванием можно упорядочить последовательность из п элементов за линейное время, если элементами рассматриваемого множества являются целые числа, заключенные между подходящими границами. Однако если эти элементы берутся из произвольного линейно упорядоченного множества, то наилучшим временем, которого мы смогли добиться, было время 0(п logп).

В данном разделе мы исследуем задачу о том, как поддержать определенную структуру в изменяющемся множестве S. Новые элементы будут добавляться к S, старые – удаляться из S, и время от времени надо будет отвечать на вопрос: "Принадлежит ли в данный момент элемент х множеству S?" Эта задача естественно моделируется словарем; нам нужна структура данных, которая позволит удобно выполнять последовательности, состоящие из операций ПРИНАДЛЕЖАТЬ, ВСТАВИТЬ и УДАЛИТЬ. Мы будем предполагать, что элементы, которые могут появиться в S, берутся из очень большого универсального множества, так что представлять S в виде двоичного вектора неразумно с практической точки зрения.

Пример 3.1. Транслятор или ассемблер следит за "таблицей символов" всех идентификаторов, которых он встретил в транслируемой программе. Для большинства языков программирования множество всех возможных идентификаторов очень велико. Например, в Фортране (старой версии, где разрешены только имена, имеющие длину не более 6 символов) около 1,6210⁹ возможных идентификаторов, в современных версиях алгоритмических языков программирования их гораздо больше. Поэтому нереально представить таблицу символов массивом с одним входом для каждого возможного идентификатора независимо от того, появляется он в программе на самом деле или нет.

Операции, производимые транслятором с таблицей символов, относятся к двум типам. Во-первых, надо добавлять в таблицу новые идентификаторы, когда они появляются. Эта работа включает в себя образование той ячейки в таблице, где запоминается конкретный идентификатор и где можно запомнить данные о нем (например, вещественный он или целый). Во-вторых, время от времени транслятор может затребовать информацию о каком-нибудь идентификаторе (например, имеет ли этот идентификатор тип "целое").

Таким образом, структура данных, способная обеспечить выполнение операций ВСТАВИТЬ и ПРИНАДЛЕЖАТЬ, вероятно, достаточна для реализации таблицы символов. И действительно, структура данных, обсуждаемая в этом разделе, часто используется для реализации таблицы символов. 

Рассмотрим способ расстановки, обеспечивающий выполнение не только операций ВСТАВИТЬ и ПРИНАДЛЕЖАТЬ, необходимых для построения таблицы символов, но и операции УДАЛИТЬ. Известно много вариантов этого способа, но здесь обсуждается только основная идея.

Схема расстановки показана на рис. 12. Функция расстановки h отображает элементы универсального множества (например, в случае таблицы символов все возможные идентификаторы) в множество целых чисел от 0 до т–1. Будем предполагать, что для всех элементов а значение h(а) можно вычислить за постоянное время. Компонентами массива А размера т служат указатели на списки элементов множества S. Список, на который указывает A[i], состоит из всех тех элементов а  S, для которых h(a)=i.

Чтобы выполнить операцию Insert(а, S), надо вычислить h(а) и затем просмотреть список, на который указывает A[h(a)]. Если элемента а в этом списке нет, его надо добавить к концу списка. Чтобы выполнить операцию Delete(а, S), надо также просмотреть список A[h(a)] и удалить элемент а, если он там есть. Аналогично просматривается список A[h(a)] и в случае операции Member(a, S).

В

Рис. 12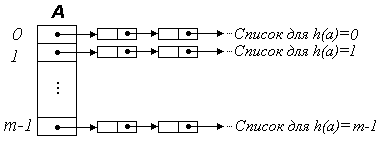

ычислительную сложность этой схемы расстановки легко проанализировать. С точки зрения работы в худшем случае она не очень хороша. Например, допустим, что последовательность о состоит из п различных операций ВСТАВИТЬ. Может случиться, что на всех элементах, которые надлежит вставить, h принимает одинаковые значения, так что все элементы оказываются в одном и том же списке. В этой ситуации для выполнения i-v. операции из  требуется время, пропорциональное i. Таким образом, чтобы добавить все п элементов к множеству S, расстановка может потребовать времени порядка n².

Однако в смысле среднего времени этот процесс выглядит много лучше. Если значение h(а) с равной вероятностью может быть любым числом между 0 и т–1 и вставляется nm элементов, то при вставке i-го элемента средняя длина того списка, в который он помещается, равна (i–1)/т, т. е. всегда меньше 1. Поэтому среднее время, необходимое для вставки п элементов, есть 0(п). Если О(п) операций УДАЛИТЬ и ПРИНАДЛЕЖАТЬ выполняются вместе с операциями ВСТАВИТЬ, то общее среднее время по-прежнему составляет 0(п).

Следует иметь в виду, что проведенный анализ предполагает, что размер т таблицы расстановки не меньше максимального размера п множества S. Однако п, как правило, заранее не известно. В таком случае разумнее всего подготовиться к построению последовательности таблиц расстановки Т₀, Т₁, Т₂, ....

Сначала выбирается подходящее значение т для размера исходной таблицы Т₀. Затем, как только число элементов, вставленных в Т₀, превзойдет m, строится новая таблица Т₁ размера 2т и с помощью новой функции расстановки (которая принимает значения от 0 до 2m–1) все элементы, находящиеся в данный момент в Т₀, перемещаются в таблицу Т₁. Теперь старая таблица Т₀ больше не нужна. Вставка новых элементов в Т₁ продолжается до тех пор, пока число элементов не превзойдет 2т. В этот момент создается новая таблица Т₂ размера 4т и меняется функция расстановки, чтобы переместить старые элементы из Т₁ в Т₂. Вообще всякий раз, когда в таблице Т_k-1 оказывается 2^k-1m элементов, строится таблица Т_k размера 2^km. Процесс продолжается до тех пор, пока не будут исчерпаны все элементы.

Подсчитаем среднее время, требуемое для вставки в таблицу расстановки 2^k элементов, если применять изложенную только что схему и считать т=1. Легко видеть, что этот процесс описывается рекуррентным уравнением

Т(1) = 1,

Т(2^k) = Т(2^k–1) + 2^k,

решением которого, очевидно, служит T(2^k) = 2^k+l – 1.

Таким образом, с помощью расстановки последовательность из п операций ВСТАВИТЬ, ПРИНАДЛЕЖАТЬ и УДАЛИТЬ можно выполнить за среднее время 0(п).

Здесь важен выбор функции расстановки h. Если элементы, добавляемые в S, представлены целыми числами, равномерно распределенными между 0 и некоторым числом r >> п, то в качестве h(a) можно взять a mod m, где т – размер таблицы расстановки в данный момент.

3.3. Двоичный поиск

В данном разделе сравниваются три различных решения одной простой задачи поиска. Дано множество S из п элементов, взятых из большого универсального множества. Требуется выполнить последовательность , состоящую только из операций ПРИНАДЛЕЖАТЬ.

Наиболее прямым путем решения было бы запомнить элементы множества S в некотором списке. Каждая операция Member(а, S) выполняется последовательными просмотрами этого списка до тех пор, пока не найдется данный элемент а или не будут просмотрены все элементы списка. Выполнение всех операций из  заняло бы тогда время порядка п как в худшем случае, так и в среднем. Основное преимущество этой схемы в том, что предварительная работа здесь занимает очень мало времени.

Другой путь – разместить элементы множества S в таблице расстановки размера S||. Операция Member(а, S) выполняется поиском в списке h(a). Если можно найти хорошую функцию h, то выполнение  займет время O(|) в среднем и O(n|) в худшем случае. Основная трудность здесь связана с нахождением функции расстановки, равномерно распределяющей элементы из S в таблице расстановки.

Если на S задан линейный порядок , то третьим решением будет двоичный поиск. Элементы из S хранятся в массиве А. Этот массив упорядочивается так, чтобы было A[1] < А[2] <  < А[п]. Теперь, чтобы установить, принадлежит ли элемент а множеству S, надо сравнить его с элементом b, который хранится в ячейке A[(1+n)/2]. Если a=b, то остановиться и ответить "да". В противном случае повторить эту процедуру на первой половине массива, если a<b, и на второй, если а>b. Повторно разбивая область поиска пополам, можно не более чем за log (n+1) сравнений либо найти а, либо установить, что его нет в S. Здесь оператор x обозначает минимальное целое число, превосходящее x.

Рекурсивная функция BinSearch(a, A, m, l), приведенная ниже, ищет элемент а в ячейках m, m+1, m+2,, l массива A. Для установления принадлежности а множеству S вызывается BinSearch(a, A, 1, n).

Чтобы понять, почему эта процедура работает, представим массив А в виде двоичного дерева. Корень находится в, ячейке (1+n)/2, а его левый и правый сыновья – в ячейках (1+n)/4 и 3(1+n)/4 соответственно, и т. д. Эта интерпретация двоичного поиска станет яснее в следующем разделе.

Легко показать, что на розыск элемента в А BinSearch тратит не более log (n+1) сравнений, так как никакой путь в рассматриваемом дереве не длиннее log (n+1). Если все элементы как цели для поиска равновероятны, то можно также показать, что BinSearch дает оптимальное среднее число сравнений (а именно, log n, необходимое для выполнения операций ПРИНАДЛЕЖАТЬ в последовательности ).

Программа 13 двоичного поиска элемента key в массиве Array

char BinSearch(char key, Array; unsigned init, fin)

{// Рекурсивная функция двоичного поиска элемента key в массиве Array. init, fin – указатели

// на первый и последний элементы массива, среди которых надо искать элемент key.

char mean; 

unsigned index;

if (fin<init) return 0; else {

index=(init+fin)>>1; mean=Array[index];

if (key==mean) return 1; else

if (key < mean) return BinSearch(key, Array, init, --index); else

return BinSearch(key, Array, ++index, fin);

}

} // Конец BinSearch

Переменная Array должна быть описана как массив того же типа, что и key. Тип char не обязателен, а может быть выбран любым, но тогда необходимо в строке  программы установить тот же тип!

Сравнивая методы двоичного поиска и расстановки, можно сказать, что поскольку в расстановке участвуют не только сравнения, то, возможно, она окажется лучше двоичного поиска (во многих случаях это действительно так).

3.4. Деревья двоичного поиска

Рассмотрим следующую задачу. В множество S вставляются и из него удаляются элементы. Время от времени может потребоваться узнать, принадлежит ли данный элемент множеству S или, например, каков в данный момент наименьший элемент в S. Cчитается, что элементы добавляются в S из большого универсального множества, линейно упорядоченного отношением . Эту задачу можно сформулировать в общем виде как выполнение последовательности, состоящей из операций ВСТАВИТЬ, УДАЛИТЬ, ПРИНАДЛЕЖАТЬ и MIN.

У

Рис. 13: Дерево двоичного поиска

же было показано, что для выполнения последовательности операций ВСТАВИТЬ, УДАЛИТЬ и ПРИНАДЛЕЖАТЬ хорошей структурой данных может служить таблица расстановки. Но нельзя найти наименьший элемент, не просмотрев всю таблицу. Структурой данных, пригодной для всех четырех операций, является дерево двоичного поиска.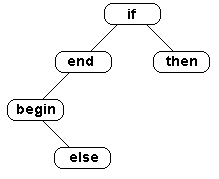

Определение. Деревом двоичного поиска (binary search tree) для множества S называется помеченное двоичное дерево, каждый узел v которого помечен элементом l(v)S так, что

1) l(u)<l(v) для каждого узла и из левого поддерева узла v,

2) l(и)>l(и) для каждого узла и из правого поддерева узла v,

3) для каждого элемента aS существует в точности один узел v, для которого l(v)=a.

Из условий 1 и 2 вытекает, что метки этого дерева расположены в соответствии с внутренним порядком. Кроме того, условие 3 следует из условий 1 и 2.

Пример 3.2. На рис. 13 изображено возможное двоичное дерево для выделенных слов алгоритмического языка PASCAL begin, else, end, if, then. Здесь линейным порядком является лексикографический порядок. 

Чтобы выяснить, принадлежит ли элемент а множеству S, представленному деревом двоичного поиска, надо сравнить а с меткой корня. Если метка корня равна а, то очевидно, что aS. Если а меньше метки корня, то надо перейти к левому поддереву корня (если оно есть). Если а больше метки корня, то надо перейти к правому поддереву корня. Если а присутствует в дереве, его местоположение будет, в конце концов, обнаружено. В противном случае процесс окончится, когда надо будет найти несуществующее левое или правое поддерево.

Алгоритм 14. Просмотр дерева двоичного поиска

Вход. Дерево Т двоичного поиска для множества S и элемент а.

Выход. "Да" (1), если aS, и "нет" (0) в противном случае.

Метод. Если дерево Т пусто, выдать "нет." В противном случае пусть r – корень дерева Т. Тогда алгоритм состоит из единственного вызова BinTreeSearch(Arrаy, r) рекурсивной процедуры BinTreeSearch, приведенной ниже.

Перед тем, как привести рассматриваемый алгоритм, сделаем несколько замечаний относительно используемых структур данных, реализующих двоичные деревья поиска.

Хотя приведенное в главе 1 определение понятия дерева требует, чтобы дерево содержало хотя бы один узел, а именно корень, во многих алгоритмах далее пустое дерево (дерево без узлов) будет трактоваться как двоичное.

С

Рис. 14.

труктура бинарного дерева построена из узлов. Узел дерева содержит поле данных и два поля с указателями. Поля указателей называются, обычно, левым указателем (left) и правым указателем (right), поскольку они указывают на левое и правое поддерево соответственно. Значение указателя NULL указывает на то, что у узла нет соответствующего сына. Если у узла оба указателя равны NULL, то это – листовой узел. На рис. 14 показаны структура одного узла (а) и способ соединения этих узлов в дерево двоичного поиска (б, в).

Далее часто алгоритмы будут приводится в общем виде на упрощенном языке, чтение которого не должно вызывать затруднений, а написание соответствующих программ остается за читателем в качестве упражнений.

Очевидно, что алгоритм 14 достаточен для выполнения операции Member(а, S). Более того, его легко модифицировать так, чтобы он выполнял операцию Insert(а, S). Если дерево пусто, строится корень с меткой а. Если дерево непусто, а элемент, который надлежит вставить, не обнаружен в дереве, то процедуре ПОИСК не удается найти сына в строке 3 или 5. Вместо того чтобы выдать "нет" в строке 4 или 6 соответственно, для этого элемента строится новый узел там, где должен был быть отсутствующий сын.

Просмотр дерева двоичного поиска.

BinTreeSearch(Arrаy, v):

1. if a=l(v) then return "1" else

2. if а<l(v) then

3. if v имеет левого сына w then return BinTreeSearch(Arrаy, w)

4. else return "0" else

5. if v имеет правого сына w then return BinTreeSearch(Arrаy, w)

6. else return "0"

Деревья двоичного поиска также удобны для выполнения операций MIN и УДАЛИТЬ. Для нахождения наименьшего элемента в дереве двоичного поиска Т просматривается путь v₀, v₁,, v_p, где v₀ – корень дерева T, v_i – левый сын узла v_i-1, l  i  p, и у узла v_p нет левого сына. Метка в узле v_p является наименьшим элементом в T. В некоторых задачах может оказаться удобным иметь указатель на v_p, чтобы обеспечить доступ к наименьшему элементу за постоянное время.

Реализовать операцию Delete(a, S) немного труднее. Допустим, что элемент а, подлежащий удалению, расположен в узле v. Возможны три случая:

1) v — лист; в этом случае v удаляется из дерева;

2) у v в точности один сын; в этом случае делаем отца узла v отцом его сына, тем самым удаляя v из дерева (если v – корень, то его сына делаем новым корнем);

3) у v два сына; в этом случае находим в левом поддереве узла v наибольший элемент b, рекурсивно удаляем из этого поддерева узел, содержащий b, и метим узел v элементом b. (Заметим, что среди элементов", меньших а, b будет наибольшим элементом всего дерева.)

Пример 3.3. На рис. 15 иллюстрируется пример удаления узла из бинарного дерева поиска. Предположим, что надо удалить узел 25 из данного дерева. Он расположен в корне, у которого два сына. Наибольшее число, меньшее 25, расположенное в левом поддереве корня,– это 15. Удаляем из дерева узел с меткой 15 и заменяем 25 на 15 в корне. Полученное дерево показано на рис. б. 

Рис. 15: Дерево двоичного поиска до (а) и после (б) выполнения операции УДАЛИТЬ (узел 25).

В качестве упражнения предлагаем написать программу на C++ для операции УДАЛИТЬ. Заметим, что одно выполнение любой из операций ПРИНАДЛЕЖАТЬ, ВСТАВИТЬ, УДАЛИТЬ и MIN можно осуществить за время О (п),

Подсчитаем временнýю сложность последовательности из п операций ВСТАВИТЬ, когда рассматриваемое множество представлено деревом двоичного поиска. Время, требуемое, чтобы в дерево двоичного поиска вставить элемент a, ограничено по порядку числом сравнений, производимых между а и элементами, уже находящимися в дереве. Поэтому время можно измерять числом производимых сравнений.

В худшем случае добавление к дереву п элементов может потребовать квадратичного времени. Например, допустим, что последовательность элементов, которые надлежит добавить, оказалась упорядоченной (в порядке возрастания). Тогда дерево поиска будет просто цепью правых сыновей. Но если вставляется п случайных элементов, то, как показывает следующая теорема, вставка потребует время 0(п log п).

Теорема 11. Среднее число сравнений, необходимых для вставка п случайных элементов в дерево двоичного поиска, пустое вначале, равно O(n log n) для n 1.

Доказательство. Пусть Т(п) – число сравнений, производимых между элементами последовательности a₁, a₂,, a_n при построении дерева двоичного поиска, T(0)=0. Пусть b₁, b₂,, b_n – та же последовательность в порядке возрастания.

Если a₁, a₂,, a_n – случайная последовательность элементов, то a₁ с равной вероятностью совпадает с b_j для любого j, 1  j  n. Элемент a_i становится корнем дерева двоичного поиска, и в окончательном дереве j–1 элементов b₁, b₂,, b_j-1 будут находиться в левом поддереве корня и п–j элементов b_j+1, b_j+2,, b_n – в правом поддереве.

Подсчитаем среднее число сравнений, необходимых для вставки элементов b₁, b₂,, b_j-1 в дерево. Каждый из этих элементов когда-нибудь сравнивается с корнем, и это дает j–1 сравнений с корнем. Затем по индукции получаем, что еще потребуется Т(j–1) сравнений, чтобы вставить b₁, b₂,, b_j-1 в левое поддерево. Итак, необходимо j–1+T(j–1) сравнений, чтобы вставить b₁, b₂,, b_j-1 в дерево двоичного поиска. Аналогично п–j+Т(п–j) сравнений потребуется, чтобы вставить в дерево элементы b_j+1, b_j+2,, b_n.

Поскольку j с равной вероятностью принимает любое значение от 1 до n, то

или, с учетом простых алгебраических преобразований,

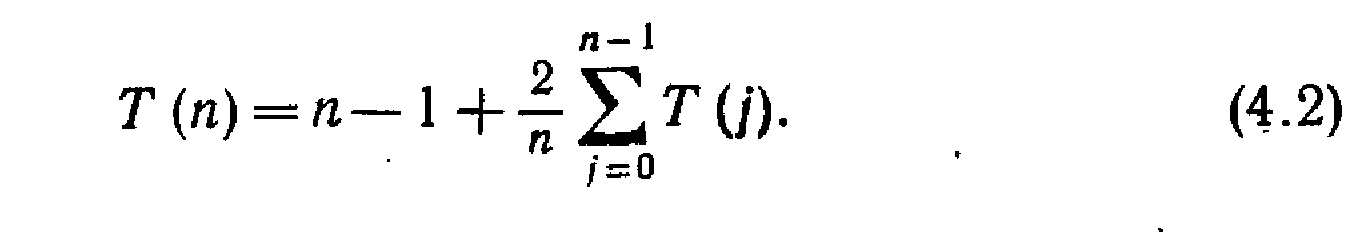
Способом, описанным в разделе 2.4, можно показать, что

где k = ln4 = 1,39. Таким образом, в среднем на вставку п элементов в дерево двоичного поиска тратится 0(п log п) сравнений. 

Итак, методами этого раздела можно выполнить случайную последовательность из п операций ВСТАВИТЬ, УДАЛИТЬ, ПРИНАДЛЕЖАТЬ и MIN за среднее время О (п log п). Выполнение в худшем случае занимает квадратичное время. Однако даже это худшее время можно улучшить до О (п log п) с помощью одной из схем сбалансированных деревьев, которые обсуждаются далее.

3.5. Оптимальные деревья двоичного поиска

В разд. 4.3 по данному множеству S={a₁, a₂,, a_n}, являющемуся подмножеством некоторого большого универсального множества U, строилась структура данных, позволяющая эффективно выполнить последовательность , составленную только из операций ПРИНАДЛЕЖАТЬ. Рассмотрим снова эту задачу, но теперь предположим, что кроме множества S задается для каждого аU вероятность появления в  операции Member(a, S). Теперь желательно построить дерево двоичного поиска для S так, чтобы последовательность  операций ПРИНАДЛЕЖАТЬ можно было выполнить в префиксном режиме с наименьшим средним числом сравнений.

Пусть a₁, a₂,, a_n –элементы множества S в порядке возрастания и p_i – вероятность появления в  операции Member(a, S). Пусть q₀ – вероятность появления в  операции Member(a, S) для некоторого а < a_i, а q_i – вероятность появления в  операции Member(a, S) для некоторого а, а_i < a < а_i+1. Наконец, пусть q_n– вероятность появления в  операции Member(a, S) для некоторого а>а_n. Для определения стоимости дерева двоичного поиска удобно добавить к нему n+1 фиктивных листьев, чтобы отразить элементы из U–S. Эти листья будут обозначаться числами 0, 1, , п.

Н

Рис. 16. Дерево двоичного поиска с добавленными листьями.

а рис. 16 показано дерево двоичного поиска, изображенное на рис. 13, с добавленными фиктивными листьями. Например, лист с меткой 3 представляет те элементы а, для которых end < a < if.

Требуется определить стоимость дерева двоичного поиска. Если элемент а равен метке l(v) некоторого узла v, то число узлов, посещенных во время выполнения операции Member(a, S), на единицу больше глубины узла v. Если aS и a_i<a<а_i+1, то число узлов, посещенных при выполнении операции Member(a, S), равно глубине фиктивного листа i. Поэтому стоимость дерева двоичного поиска можно определить как

,

где depth() – глубина соответствующего узла дерева.

Теперь, если есть дерево двоичного поиска Т, обладающее наименьшей стоимостью, можно выполнить последовательность операций ПРИНАДЛЕЖАТЬ с наименьшим средним числом посещений узлов, просто применив для выполнения каждой операции ПРИНАДЛЕЖАТЬ алгоритм 14 на T.

Если даны числа p_i и q_i, то как найти дерево наименьшей стоимости? Подход "разделяй и властвуй" предлагает определить элемент a_i, который надо поставить в корень. Это разбило бы данную задачу на две подзадачи: построение левого и правого поддеревьев. Однако, похоже, нет легкого пути определения корня без решения всей задачи. Поэтому придется решать 2п подзадач: по две для каждого возможного корня. Это естественно приводит к решению с помощью динамического программирования.

Для 0i<jn обозначим через Т_ij дерево наименьшей стоимости для подмножества {a_i+1, a_i+2, , a_j}. Пусть c_ij – стоимость дерева Т_ij, а r_ij – его корень. Вес w_ij дерева Т_ij определяется как q_i + (p_i+1 + q_i+1)+  +(p_j + q_j).

Дерево T_ij состоит из корня a_k, левого поддерева Т_i,k–1 (т. е. дерева наименьшей стоимости для {a_i+1, a_i+2, , a_k–1}) и правого Т_kj (т. е. дерева наименьшей стоимости для {a_k+1, a_k+2, , a_j}) (рис. 17). Если i=k–1, то нет левого поддерева, а при k=j нет правого поддерева. Для удобства Т_ii будет трактоваться как пустое дерево. Вес w_ii дерева Т_ii равен q_i, а его стоимость c_ii равна 0.

В

Рис. 17: Поддерево Т_ij.

Т_ij, i<j, глубина каждого узла в левом и правом поддеревьях на единицу больше глубины того же узла в Т_i,k–1 или Т_kj. Поэтому стоимость c_ij дерева Т_ij можно выразить так:

c_ij=w_i,k–1+p_k+ w_kj+ c_i,k–1+c_kj = w_ij + c_i,k–1+c_kj.

Следует брать здесь то значение k, которое минимизирует сумму c_i,k–1+c_kj. Поэтому для нахождения оптимального дерева Т_ij вычисляют для каждого k, i < k  j, стоимость дерева с корнем a_k, левым поддеревом Т_i,k–1, и правым поддеревом Т_kj, а затем выбирают дерево наименьшей стоимости. Приведем соответствующий алгоритм.

Алгоритм 15. Построение оптимального дерева двоичного поиска

Вход. Множество S вида {a₁, a₂, , a_n}, где a₁<a₂<<.a_n Известны также вероятности q₀, q₁,, q_n и p₁,, p_n, где q_i, 1 i<n, – вероятность выполнения операции Member(a, S) для a_i<a<a_i+1, q₀ – вероятность выполнения операции Member(a, S) для а<а₁, q_n – вероятность выполнения операции Member(a, S) для a>a_n, a p_i, 1in, – вероятность выполнения операции Member(a, S).

Выход. Дерево двоичного поиска для S, обладающее наименьшей стоимостью.

Метод.

1. Для 0i<jn вычисляются r_ij и c_ij в порядке возрастания разности j–i с помощью алгоритма динамического программирования.

Алгоритм динамического программирования нахождения корней оптимальных поддеревьев.

begin

1. for i=0 until n do

begin

2. w_ii=q_i

3. c_ii=0

end;

4. for l= 1 until n do

5. for i=0 until n–l do

begin

6. j=i+l;

7. w_ij = w_i,j–1 + p_j + q_j;

8. пусть m – значение k, i < k  l, для которого сумма c_i,k–1+c_kj минимальна;

9. c_ij = w_i,j + c_i,m–1+c_mj;

10. r_ij=a_m,

end

end

2. После вычисления всех r_ij вызывается функция BuildTree(0, п) для рекурсивного построения оптимального дерева для T_0n.

Функция для построения оптимального дерева двоичного поиска.

BuildTree(i, j):

begin

образовать корень vij дерева Tij;

пометить vij меткой rij;

пусть m – индекс числа rij (т. е. rij=am);

if i<m–1 then сделать BuildTree(i, m–1) левым поддеревом узла vij;

if m<j then сделать BuildTree(т, j) правым поддеревом узла vij

end \ 

Пример 3.4. Рассмотрим четыре элемента а₁<а₂<а₃<а₄ с q₀=1/8, q₁=3/16, q₂= q₃= q₄=1/16 и p₁=1/4, p₂=1/8, p₃= p₄=1/16. В таблице даны значения w_ij, r_ij и c_ij, вычисленные приведенным алгоритмом нахождения корней оптимальных поддеревьев. Для удобства записи значения w_ij и c_ij в этой таблице были умножены на 16.

Таблица 10: Значения w_ij, r_ij и c_ij

w Рис. 18: Дерево наименьшей стоимости. 00=2 c00=0	w11=3 c11=0	w22=1 c22=0	w33=1 c33=0	w44=1 c44=0
w01=9 c01=9 r01=a1	w12=6 c12=6 r12=a2	w23=3 c23=3 r23=a3	w34=3 c34=3 r34=a4
w02=12 c02=18 r02=a1	w13=8 c13=11 r13=a2	w24=5 c24=8 r24=a4
w03=14 c03=25 r03=a1	w14=10 c14=18 r14=a2
w04=16 c04=33 r04=a2

Например, чтобы вычислить r₁₄, надо сравнить значения c₁₁+c₂₄, c₁₂+c₃₄ и c₁₃+c₄₄, равные (после умножения на 16) соответственно 8, 9 и 11. Таким образом, в строке 8 алгоритма k=2 дает минимум, так что r₁₄=a₂.

Заполнив таблицу 10, строим дерево Т₀₄, вызывая BuildTree(0, 4). На рис. 18 изображено полученное в результате дерево двоичного поиска. Его стоимость равна 33/16. 

Теорема 12. Алгоритм 15 строит оптимальное дерево двоичного поиска за время O(n³).

Доказательство. Вычислив таблицу значений r_ij, по ней строят оптимальное дерево за время О(п), вызывая процедуру BuildTree. Эта процедура вызывается только п раз, и каждый вызов занимает постоянное время.

Наиболее дорого стоит алгоритм динамического программирования. Строка 8 находит значение k, минимизирующее c_i,k–1+c_kj, за время O(j–i). Остальные шаги цикла в строках 5–10 занимают постоянное время. Внешний цикл в строке 4 выполняется п раз, внутренний – не более п раз для каждой итерации внешнего цикла. Таким образом, суммарная сложность составляет 0(п³).

Что касается корректности алгоритма, то простой индукцией по l=j–i можно показать, что r_ij и c_ij правильно вычисляются в строках 9 и 10.

Чтобы показать, что оптимальное дерево правильно строится процедурой BuildTree, заметим, что если v_ij – корень поддерева для {a_i+1, a_i+2, , a_j}, то его левый сын будет корнем оптимального дерева для {a_i+1, a_i+2, , a_m–1}, где r_ij=а_m, а правый будет корнем оптимального дерева для {a_m+1, a_m+2, , a_j}.

Теперь должно быть ясно, как доказать по индукции, что процедура BuildTree(i, j) правильно строит оптимальное дерево для {a_i+1, a_i+2, , a_j}. 

В алгоритме 15 можно ограничить поиск т в строке 8 областью между положениями корней деревьев T_i,j–1 и T_i+1,j, при этом гарантируется нахождение минимума. Тогда алгоритм 15 сможет находить оптимальное дерево за время 0(п²).

3.6. Простой алгоритм для нахождения объединения непересекающихся множеств

Часто во многих приложениях возникают задачи, которые имеют дело с непересекающимися множествами, содержащими счетные количества элементов, в которых нужно бывает отыскивать какие-то элементы и объединять различные множества. Тогда задача преобразования множеств обладает следующими тремя особенностями.

1. Всякий раз сливаются только непересекающиеся множества.

2. Элементы множеств можно считать целыми числами от 1 до п.

3. Операциями над множествами являются ОБЪЕДИНИТЬ и НАЙТИ.

Изучим структуры данных для задач такого типа. Пусть даны п элементов, которые будут считаться целыми числами 1, 2, , п. Предположим, что вначале каждый элемент образует одноэлементное множество. Пусть надо выполнить последовательность операций ОБЪЕДИНИТЬ и НАЙТИ. Напомним, что операция ОБЪЕДИНИТЬ имеет вид Union(A, B, C), указывающий, что два непересекающихся множества с именами А и В надо заменить их объединением и назвать это объединение С. В приложениях часто неважно, что выбирается в качестве имени множества, так что будем предполагать, что множества можно именовать целыми числами от 1 до п. Кроме того, будем предполагать, что никакие два множества ни в один момент не названы одинаково.

Эту задачу позволяют решить несколько интересных структур данных. В этом разделе познакомимся со структурой данных, благодаря которой можно выполнить за время О(пlogп) последовательность, содержащую до п–1 операций ОБЪЕДИНИТЬ и до О(пlogп) операций НАЙТИ. В следующем разделе будет описана структура данных, позволяющая обрабатывать последовательность из 0(п) операций ОБЪЕДИНИТЬ и НАЙТИ в худшем случае за время, почти линейное по n. Эти структуры данных могут обрабатывать последовательности операций ВСТАВИТЬ, УДАЛИТЬ и ПРИНАДЛЕЖАТЬ с той же вычислительной сложностью.

Заметим, что в алгоритмах поиска, изложенных в разд. 3.2-3.5, предполагалось, что элементы выбираются из универсального множества, много большего, чем множество выполняемых операций. В этом разделе универсальное множество будет приблизительно того же размера, что и длина последовательности выполняемых операций.

По-видимому, простейшей структурой данных для задачи типа ОБЪЕДИНИТЬ – НАЙТИ служит массив, представляющий набор множеств в данный момент. Пусть R – массив размера п, a R[i] – имя множества, содержащего элемент i. Так как вид имен множеств не существен, можно вначале взять R[i]=i, l  i  n, и выразить тем самым факт, что перед началом работы набором множеств является {{1}, {2}, , {п}} и множество {i} имеет имя i.

Операция Find(i) выполняется путем печати значения R[i] в данный момент. Поэтому сложность выполнения операции НАЙТИ постоянна, а это лучшее, на что можно надеяться.

Чтобы выполнить операцию Union(A, B, C), надо последовательно просмотреть массив R и заменить каждую его компоненту, равную А или В, на С. Поэтому сложность выполнения такой операции есть О(п). Последовательность из п операций ОБЪЕДИНИТЬ могла бы потребовать О(п²) времени, что нежелательно.

Этот безыскусный алгоритм можно улучшить несколькими способами. Для одного улучшения можно воспользоваться преимуществом связанных списков. Для другого – понять, что всегда эффективнее влить меньшее множество в большее. Чтобы сделать это, надо отличать "внутренние имена", используемые для идентификации множеств в массиве R, от "внешних имен", упоминаемых в операциях ОБЪЕДИНИТЬ. И те, и другие предполагаются числами от 1 до п, но не обязательно одинаковыми.

Рассмотрим следующую структуру данных для этой задачи. Как и ранее, возьмем такой массив R, что R[i] содержит "внутреннее" имя множества, которому принадлежит элемент i. Но теперь для каждого множества А можно построить связанный список List[A], содержащий его элементы. Для реализации этого связанного списка применяются два массива List и Next. List[A] представляет собой целое число j, указывающее, что j – первый элемент в множестве с внутренним именем A. Next[j] дает следующий элемент в А, Next[Next[j]] – следующий за ним элемент, и т. д.

К

Рис. 19: Структуры данных для алгоритма

Объединить–Найти.

роме того, возьмем еще массив, называемый Size (РАЗМЕР), такой, что Size[A] – число элементов в множестве А. Множества будут переименовываться по внутренним именам, а два массива In_Name (Внутреннее имя) и Out_Name (Внешнее имя) будут устанавливать соответствие между внутренними и внешними именами. Иными словами, Out_Name[А] – это настоящее имя (диктуемое операциями ОБЪЕДИНИТЬ) множества с внутренним именем А. In_Name[j] – это внутреннее имя множества с внешним именем j. Внутренние имена – это имена, используемые в массиве R.

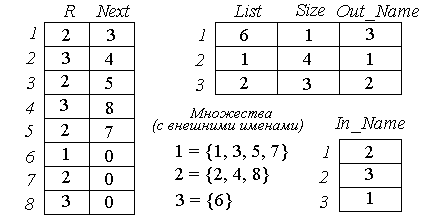
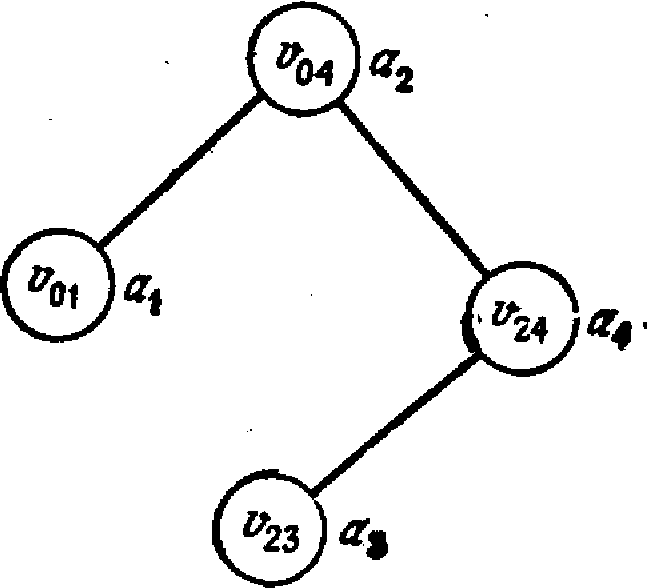
Пример 3.5. Пусть n=8 и у нас есть набор из трех множеств {1, 3, 5, 7}, {2, 4, 8} и {6} с внешними именами 1, 2 и 3 соответственно. Структуры данных для этих трех множеств показаны на рис. 19, где 2,3 и 1 — внутренние имена для 1,2 и 3 соответственно. 

Операция Find(i) выполняется, как и раньше, обращением к R[i] для установления внутреннего имени множества, содержащего элемент i в данный момент. Затем Out_Name[R[i]] дает настоящее имя множества, которому принадлежит i.

Операцию объединения вида Union(I, J, K) выполняется с помощью алгоритма 16. (Номера строк относятся к процедуре алгоритма).

Алгоритм 16. Реализация операции ОБЪЕДИНИТЬ

1. Определяем внутренние имена для множеств I и J (строки 1, 2).

2. Сравниваем относительные размеры множеств I и J, справляясь в массиве Size (строки 3, 4).

3. Проходим список элементов меньшего множества и изменяем соответствующие компоненты в массиве R на внутреннее имя большего множества (строки 5–9).

4. Вливаем меньшее множество в большее, добавляя список элементов меньшего множества к началу списка для большего множества (строки 10–12).

5. Присваиваем полученному множеству внешнее имя К (строки 13, 14).

Вливая меньшее множество в большее, мы делаем время выполнения операции ОБЪЕДИНИТЬ пропорциональным мощности меньшего множества. Все детали приведены в процедуре алгоритма.

Функция, реализующая операцию ОБЪЕДИНИТЬ

Union(I, J, K)

begin

1.А=In_Name[I];

2.B=In_Name[I];