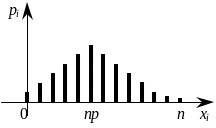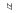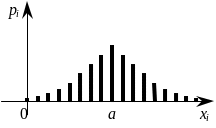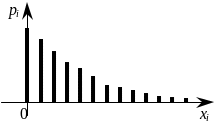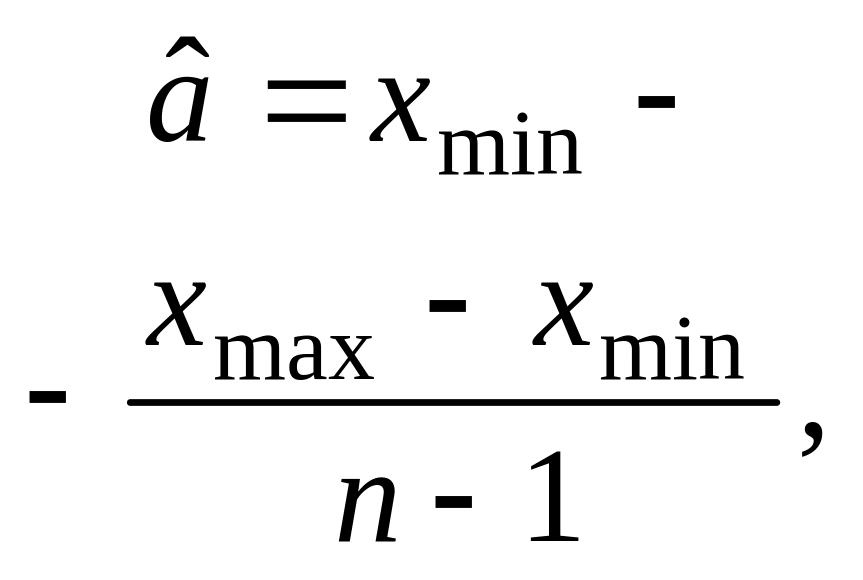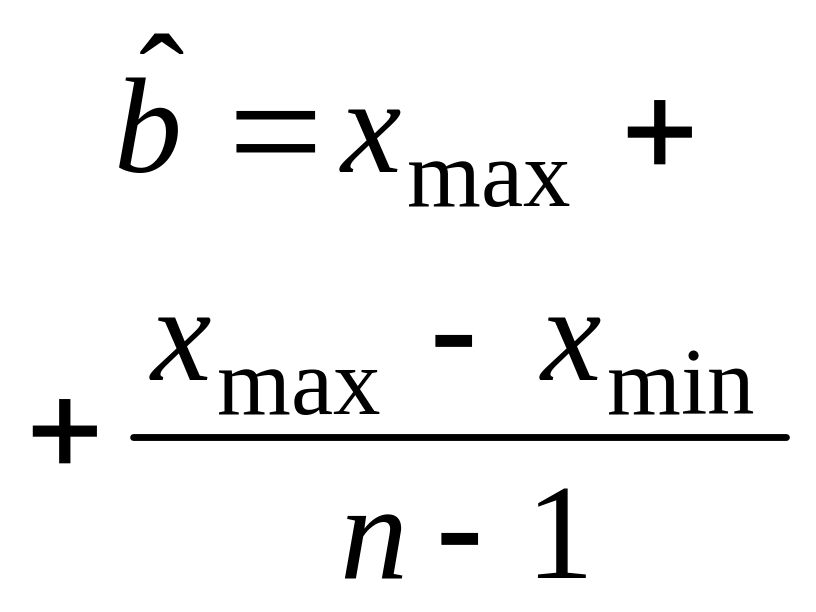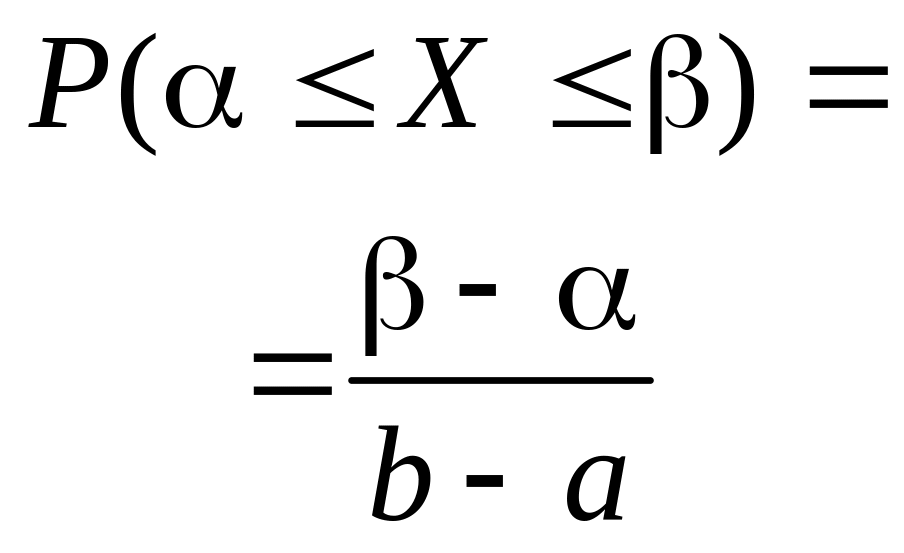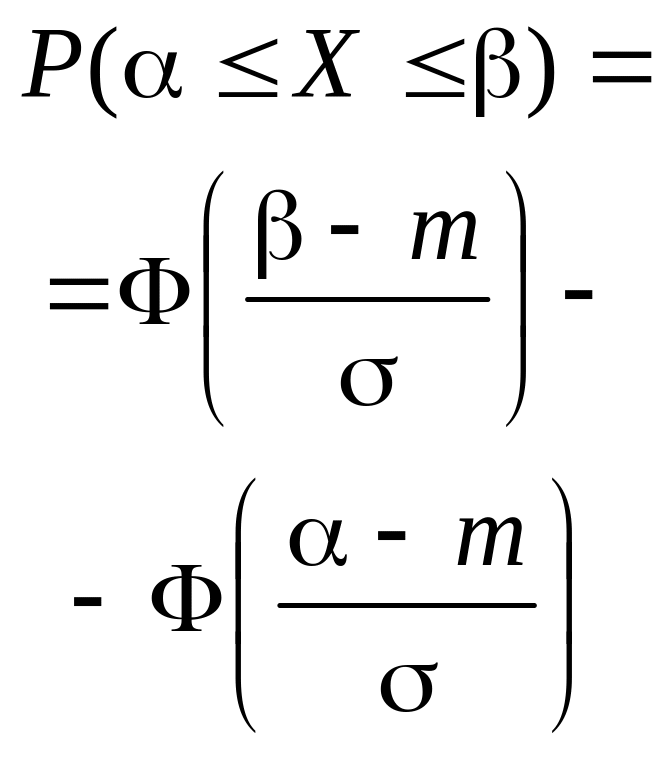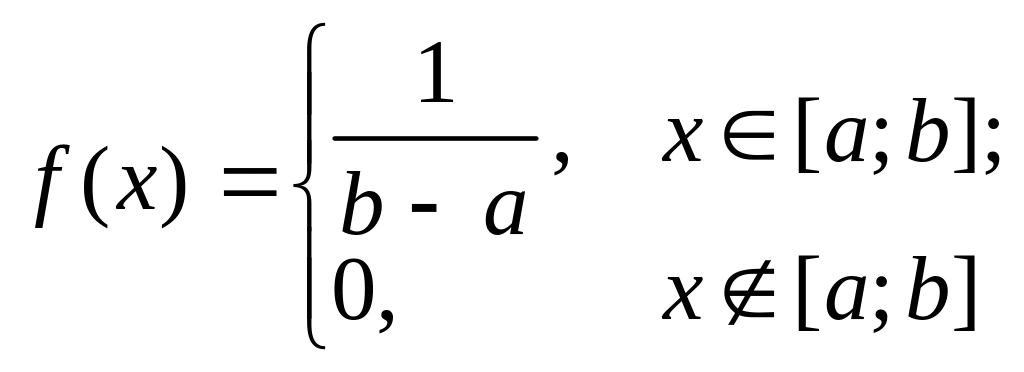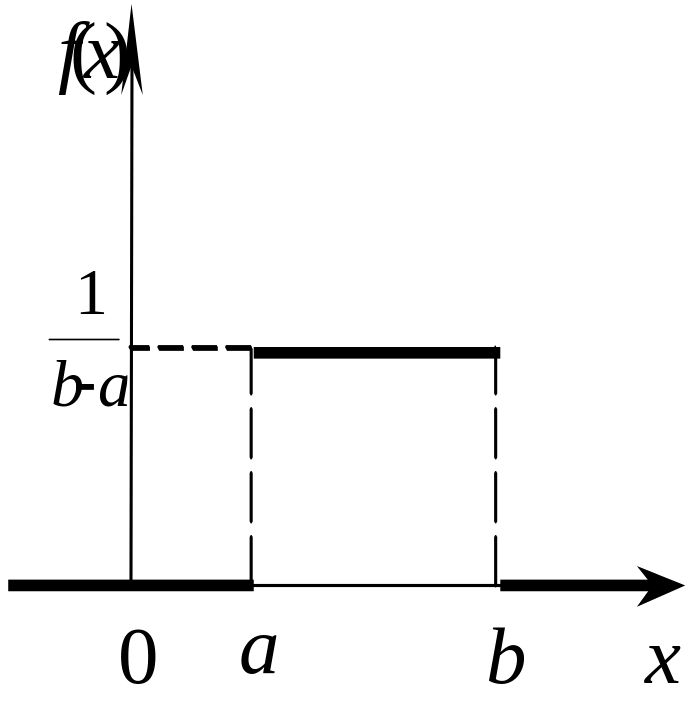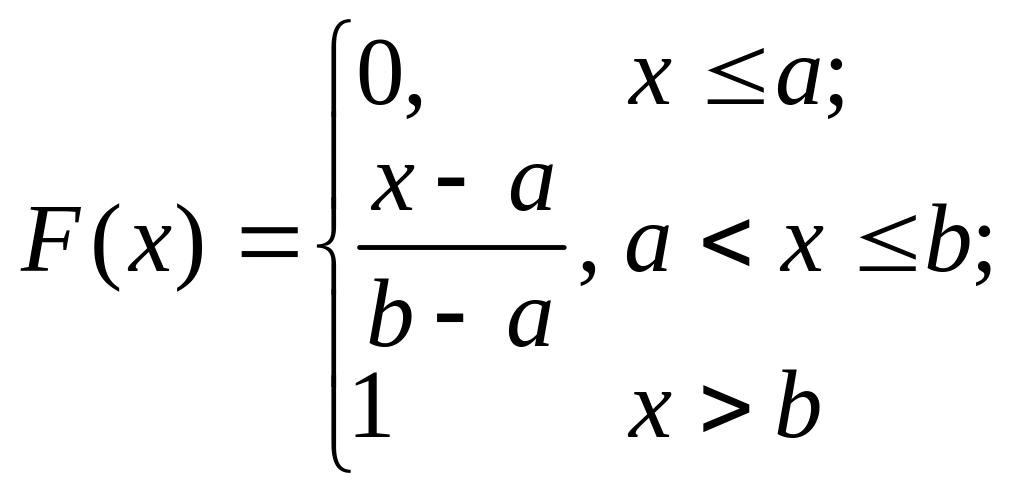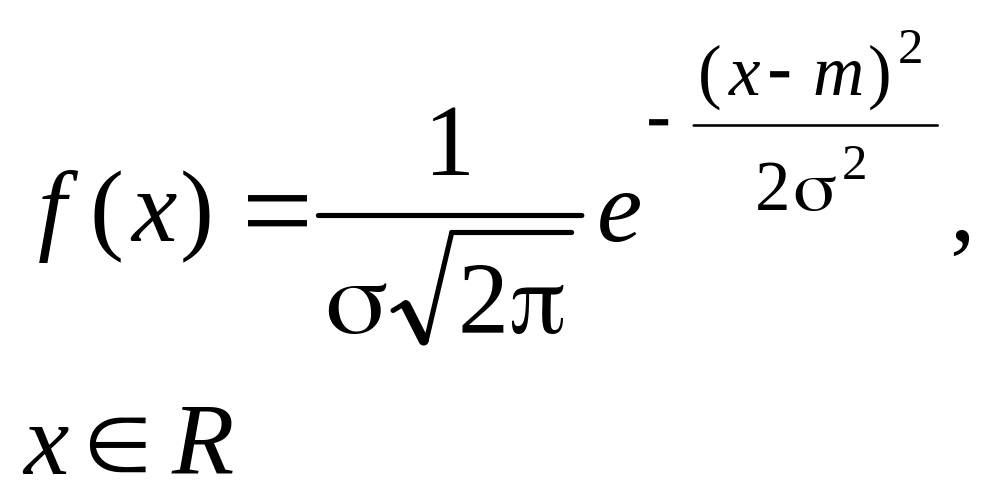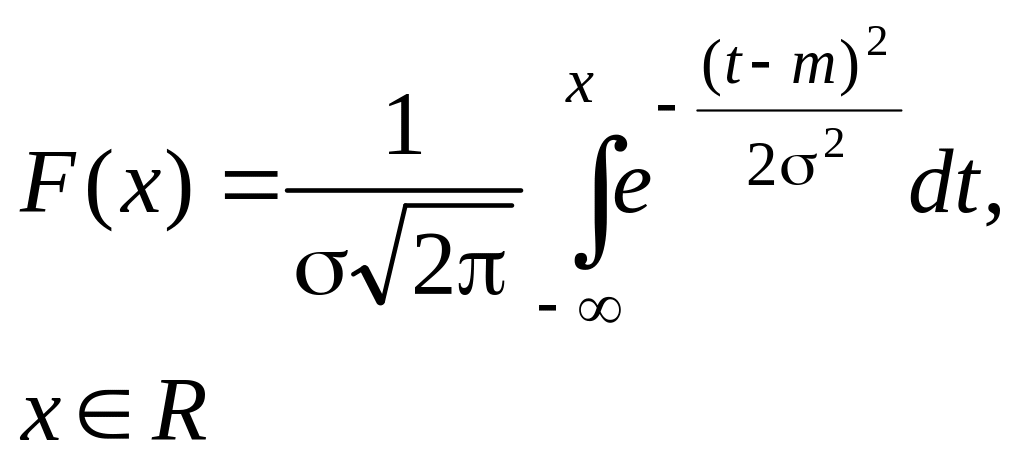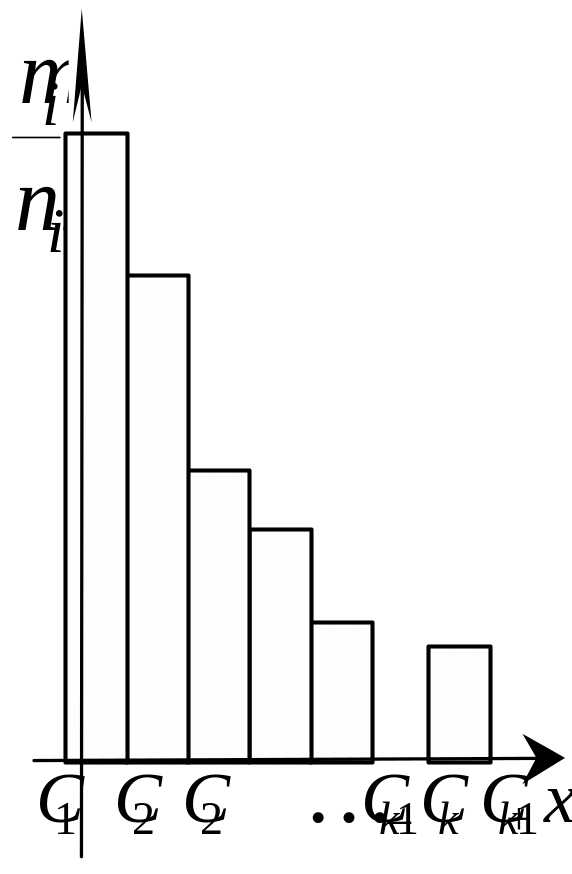3 Применение критерия Пирсона 2 для проверки гипотезы о виде закона распределения случайной величины

Гипотеза о виде закона распределения изучаемой случайной величины обычно выдвигается на основании графического изображения статисти-ческого закона распределения, сведений о механизме формирования значений этой величины, а также на основании значений оценок числовых характеристик.

В таблицах 1 и 2 приведены сведения о наиболее часто используемых при решении практических задач законах распределения дискретных и непрерывных случайных величин. В графе «Примечание» этих таблиц приведены примеры случайных величин, подчиняющихся указанным законам, либо описан механизм формирования значений этих величин.

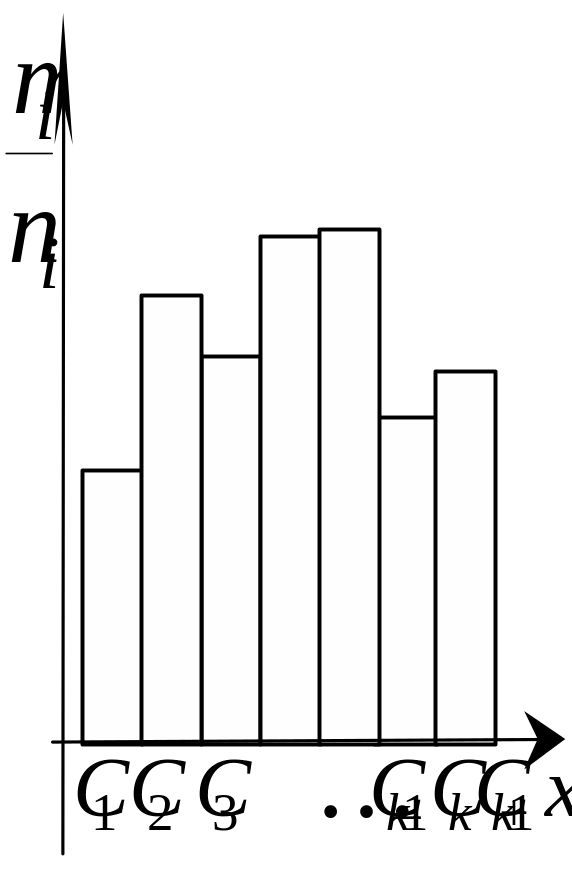
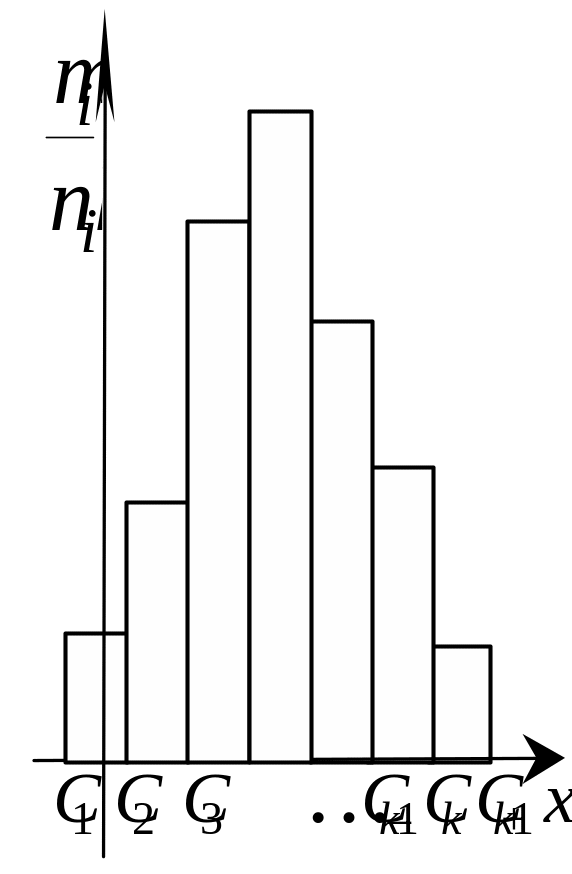
Если изучается непрерывная случайная величина, то вид гистограммы относительных частот обычно значительно облегчает задачу выдвижения гипотезы H₀. Например, по виду гистограммы, изображённой на рисунке 1, а, логично выдвинуть гипотезу о равномерном законе распределения исследуемой случайной величины. Вид гистограмм, приведённых на рисунках 1, б и 1, в, напоминает соответственно кривые экспоненциального и нормального законов распределения. Большое внимание при выдвижении гипотез уделяется и вычисленным значениям числовых характеристик (примеры 1, 2).

Таблица 1 – Основные сведения о наиболее часто встречающихся на практике законах распределения дискретных случайных величин

Название закона распределения	Возможные значения	Параметры	Параметры	Числовые характеристики			Вероятности возможных значений, столбцовая диаграмма	Примечание
				M[X]	D[X]	[X]
Биномиальный	X = 0, 1, 2, ..., n	p, n						Случайная величина X характеризует число появлений события A в серии из n независимых испытаний, в каждом из которых это событие может осуществиться с вероятностью p
Пуассона	X = 0, 1, 2, ..., m, ...	a						Пример: число событий простейшего потока, характеризующегося интенсивностью a, где a – число событий, произошедших в течение единицы времени
Геометрический	X = 0, 1, 2, ..., m, ...	p						Случайная величина X характеризует число независимых испытаний, произведённых до первого появления события A, которое в каждом из этих испытаний может произойти с вероятностью p (при этом испытание, в котором появляется событие A, не учитывается)

Таблица 2 – Основные сведения о наиболее часто встречающихся на практике
Закон распре-деления	Возможные значения	Пара­метры	Статистическая оценка параметров	Числовые характеристики					Вероятность попадания значений с. в. в отрезок [; ]
				M[X]	D[X]	[X]	A[X]	Ex[X]
Равно-мерный		a b					0	–1,2
Экспо-ненци-альный (показа-тельный)							2	6
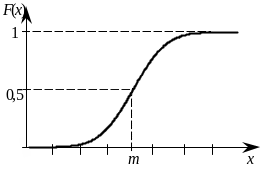
Нормаль-ный		m 		m	2		0	0

Проверка гипотезы о предполагаемом распределении производится с помощью непараметрических критериев значимости. Одной из групп таких критериев значимости являются критерии согласия, с помощью которых проверяются нулевые гипотезы о виде функции распределения случайной величины.

Одним из наиболее широко используемых на практике критериев согласия является критерий ² Пирсона. Он может использоваться для проверки гипотез о виде закона распределения как дискретных, так и непрерывных случайных величин.

законах распределения непрерывных случайных величин
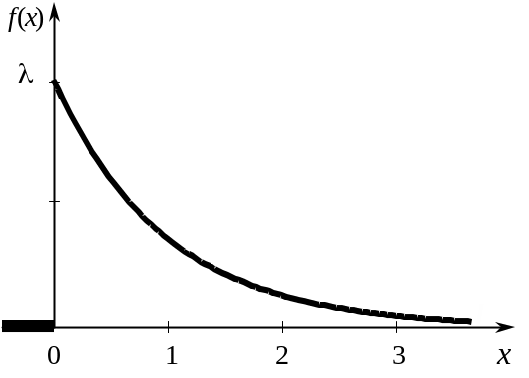
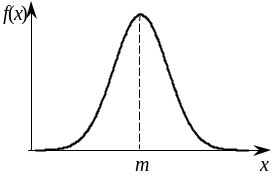
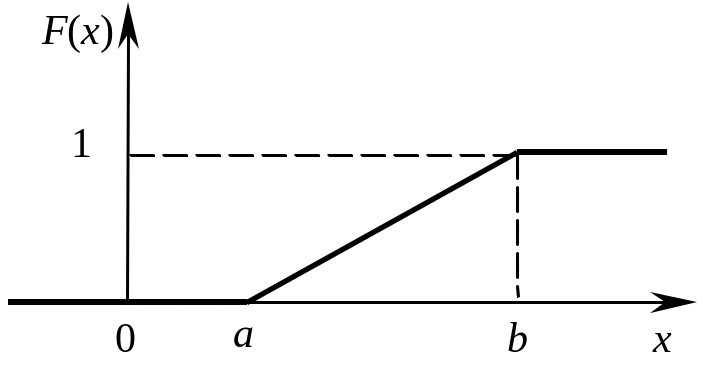
Функция плотности распределения вероятностей	Функция распределения	Примечание
		Если все возможные значения непрерывной случайной величины принадлежат отрезку [a; b], и все значения, попадающие на этот отрезок равновозможны, то данная случайная величина X распределена по равномерному закону. Пример: величина погрешности при округлении данных
		Примеры: – промежуток времени между моментами наступления двух последовательных событий простейшего потока; – разнообразные временные характеристики функционирования технических устройств (время безотказной работы оборудования и т. д.)
		Если случайная величина X представляет собой сумму большого числа независимых (или слабо зависимых) случайных величин, сопоставимых по уровню своего влияния на суммарный результат, то эта величина имеет распределение, близкое к нормальному Пример: реальные значения параметров изготовленного изделия

Применение критерия ² основано на сопоставлении эмпирических m_i и теоретических np_i (вычисленных в предположении справедливости проверяемой гипотезы) частот попадания значений исследуемой случайной величины в рассматриваемые частичные разряды. В качестве меры расхождения эмпирического и теоретического распределений используется статистика

, (1)

которая при независимо от вида предполагаемого распределения стремится к распределению ² с степенями свободы (здесь – число разрядов разбиения, r – число параметров теоретического распределения, оцениваемых по выборке).

Легко заметить, что при незначительных отклонениях значений m_i от np_i значение критерия ² будет близким к нулю. И наоборот, большое значение критерия ² свидетельствует о существенном отклонении значений m_i и np_i.

а)
б)		в)
	Рисунок 1 – Примеры гистограмм относительных частот

Необходимыми условиями применения критерия ² являются достаточно большой объем выборки (n  30) и отсутствие в теоретическом распределении разрядов с небольшим (np_i < 5) числом наблюдений. Для обеспечения последнего условия интервалы, для которых np_i < 5, необходимо объединить с соседними. На хвостах распределения допускается значение np_i   1.